gtr022001 wrote:
VeritasPrepKarishma wrote:
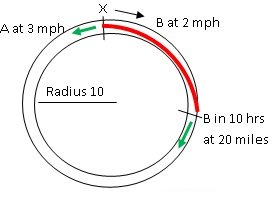
Radius of track is 10 miles so circumference is 20*pi i.e. the total length of the track.
B starts from X and travels for 10 hrs clockwise at 2 mph i.e. it travels 20 miles. Now car A starts from X counter clockwise. Distance between A and B is 20*pi - 20.
Now, to meet, they have to together cover this distance plus 12 miles more which they have to put between them.
Time taken to cover this distance by them = (20*pi - 20 + 12)/(3 + 2) = 4*pi - 1.6 hrs
Car B has been traveling for 10 + 4*pi - 1.6 = (4*pi + 8.4) hrs
Hi Karishma, i actually got this question wrong when i took the
mgmat cat last week, i got confused on the explanation which is similar to yours (your diagram helps though), how did you derive this equation: (20*pi - 20 + 12)/(3 + 2), was this manipulated from Rate x Time = Distance? thanks.
Attachment:
 Ques1.jpg [ 14.88 KiB | Viewed 57784 times ]
Ques1.jpg [ 14.88 KiB | Viewed 57784 times ]
The red distance is what B has already covered at 2 mph in 10 hrs. This distance is 20 miles.
A and B are now moving towards each other (as shown by green arrows). To meet for the first time, they have to cover the remaining circumference of the track i.e. a distance of 20pi - 20. (20pi is the circumference of the circle out of which 20 has already been covered by B). They need to create a further 12 miles distance between them. So together they need to cover (20pi - 20 + 12) miles in all.
Since, A and B are moving towards each other, their relative speed (i.e. combined speed here) will be (3 + 2) mph.
So time taken for them to meet = D/S = (20pi - 20 + 12)/(3 + 2)
- Here, we are using the concept of Relative Speed. When two objects (speeds S1 and S2) move in opposite directions (towards each other or away from each other), they cover the distance between them (or create distance between them) at the rate of (S1 + S2). Here they are moving in opposite directions towards each other so their relative speed is sum of their speeds. After meeting, they are moving away from each other but their relative speed is still sum of their speeds.
When two objects move in same direction, their speeds get subtracted.
If this is unclear, I would suggest looking up the theory of relative speed for details.
Check this video for when to use relative speed:
https://youtu.be/wrYxeZ2WsEM _________________
Karishma Bansal - ANA PREP
*SUPER SUNDAYS!* - FREE Access to ALL Resources EVERY Sunday
REGISTER at ANA PREP
(Includes access to Study Modules, Concept Videos, Practice Questions and LIVE Classes)
YouTube Channel
youtube.com/karishma.anaprep



 95%
(hard)
95%
(hard)
 52%
(03:09)
wrong
52%
(03:09)
wrong  based on 1290
sessions
based on 1290
sessions









