gmatbull wrote:
If f(x) = 2^(x) + 2^(-2), and x is an integer, is f(x) = √(a + 4)?
(1) -4 < x < 4
(2) 4^(x) + 4^(-x) = a
An interesting DS problem. The prompt involves this letter
a, and if we don't know the value of this, then we can't determine anything.
For
Statement #1, without doing any calculations, we see that not matter what range is established for x, we have no idea what
a is, and without some indication of the value of
a, we have no way of answering the prompt question. Statement #1, alone and by itself, is
insufficient.
Statement #2 is interesting
For example, let's consider x = 0
Then f(0) = 1 + 1/4 = 5/4 = 1.25
Meanwhile, sqrt(4^(x) + 4^(-x) + 4) = sqrt(1 + 1 + 4) = sqrt(6). For that value, they are not equal.
Let's consider x = 1
Then f(1) = 2 + 1/4 = 9/4 = 2.25
Meanwhile, sqrt(4^(x) + 4^(-x) + 4) = sqrt(4 + 1/4 + 4) = sqrt(33/4) = [sqrt(33)]/2. For that value they are not equal.
Let's set the two expressions equal and see what happens:
2^(x) + 2^(-2) = sqrt(4^(x) + 4^(-x) + 4)
square both sides
(2^x)^2 + 2*(2^x)*(2^(-2)) + (2^(-2))^2 = 4^(x) + 4^(-x) + 4
4^(x) +(1/2)*(2^x) + 1/16 =
4^(x)+ 4^(-x) + 4
(1/2)*(2^x) + 1/16 = 4^(-x) + 4
(1/2)*(2^x) - 4^(-x) = 4 - 1/16
(1/2)*(2^x) - 4^(-x) = 63/16
There are really no straightforward algebraic ways to simplify this. Let g(x) = sqrt(4^(x) + 4^(-x) + 4). Looking at a graph of f(x) & g(x), we see that the functions appear to approach each other asymptotically as x gets large in the positive direction.
Attachment:
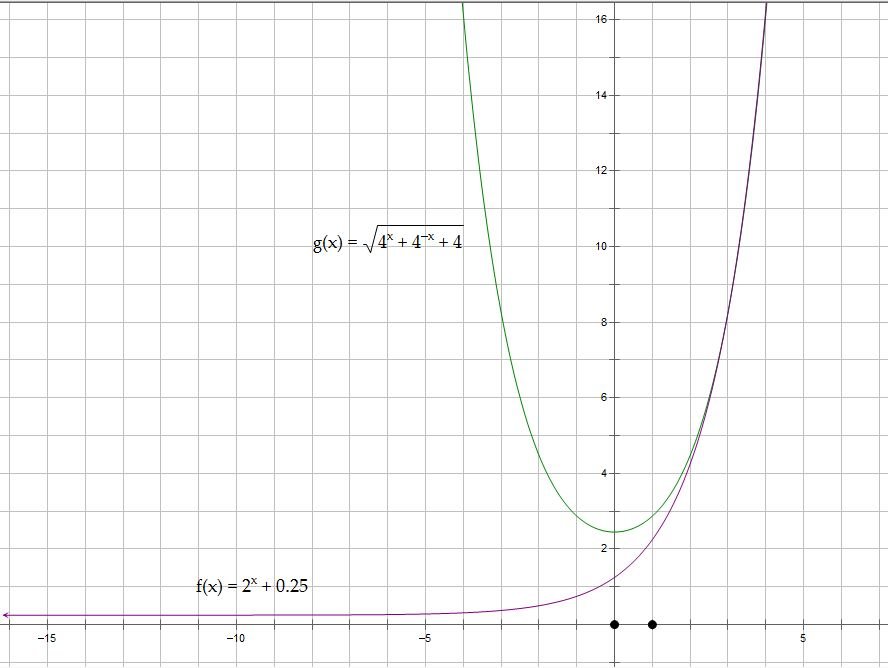graph of f(x) & g(x).JPG [ 75.08 KiB | Viewed 352 times ]
In fact, the two functions actually cross at x = 2.9831285117658, and asymptotically approach each other thereafter
Given that x has to be an integer, the two expressions will never be equal.
Therefore, despite what the above post says is the OA, it seems to me the answer must be
B. It's really not clear to me that there's an efficient way to solve this without substantial recourse to technology.
Notice that if the function in the prompt were
f(x) = 2^(x) + 2^(-x) instead of
2^(x) + 2^(-2), and the expression in the prompt were
f(x) = √(a + 2) instead of
f(x) = √(a + 4), then the expressions would always be equal, for all real numbers.
Does all this make sense?
Mike
_________________
Mike McGarry
Magoosh Test Prep
close
33% (00:00) correct
