In the xy-plane, region R consists of all the points (x, y)

Although there are too good solutions, here's my take.
If you are good with drawing lines, this question would be easier to solve.
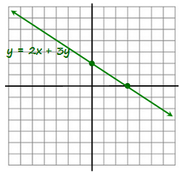
Region R for \(2x + 3y =< 6\) would lie below the line \(2x + 3y = 6\), the side on which origin(as it satisfies the condition) lies. For the condition to be satisfied the most important thing is that the line must be parallel(equal slopes) to \(2x + 3y = 6\) and region is clearly defined i.e. either <6 or >6. Let's see what we have.

(1) \(3r + 2s = 6\)
Without doing much math we can eliminate options A and D. Because the coefficients of r and s are different from that of line \(2x + 3y = 6\) - 3 for r/2 for x and 2 for s/3 for y - the two lines would intersect. Thus, suggesting that a part of line \(3r + 2s = 6\) would be on the other side of the line \(2x + 3y = 6\). Hence some points would satisfy the condition and some would not.

OR

If we write the two line equation in the form y = mx + c, we can say that the two lines have different slopes - -\(\frac{2}{3}\) and -\(\frac{3}{2}\). \(y = -\frac{2}{3}x + 2\) and \(s = -\frac{3}{2}r + 3\), suggesting that the two lines intersect.

In any case, we need not to check points.
(Note: RHS of the equation i.e. 6 makes no sense here as you can see the slopes are different. Had the value been <6 again then it would not have been again sufficient.)

INSUFFICIENT.

(2) \(r=< 3\) and \(s=< 2\)
Again, applying the similar theory we see that some points would not satisfy(r = 3 and s = 2) the condition and some would(r = -3 and y = -2).
Eliminate option B.

INSUFFICIENT.

Combined together statement 1 and 2.
Refer screenshot:

We are left with the condition r ≤ 3, 3r+2s = 6 and s ≤ 2. The are still many points that satisfy the condition and many don't.
The triangular region with 3 different colored dots invalidate the condition and rest satisfy the condition.

Answer E.