Math: Triangles

		00:00
	GMAT Timer...

TRIANGLES

This post is a part of [GMAT MATH BOOK]

created by: Bunuel
edited by: bb, walker

--------------------------------------------------------


This topic is included in GMAT ToolKit App (iPhone/iPod Touch)
[read more] [AppStore]



--------------------------------------------------------

Triangle A closed figure consisting of three line segments linked end-to-end. A 3-sided polygon.



Vertex The vertex (plural: vertices) is a corner of the triangle. Every triangle has three vertices.


Base The base of a triangle can be any one of the three sides, usually the one drawn at the bottom.

• You can pick any side you like to be the base.
• Commonly used as a reference side for calculating the area of the triangle.
• In an isosceles triangle, the base is usually taken to be the unequal side.


Altitude The altitude of a triangle is the perpendicular from the base to the opposite vertex. (The base may need to be extended).


• Since there are three possible bases, there are also three possible altitudes.
• The three altitudes intersect at a single point, called the orthocenter of the triangle.


Median The median of a triangle is a line from a vertex to the midpoint of the opposite side.


• The three medians intersect at a single point, called the centroid of the triangle.
• Each median divides the triangle into two smaller triangles which have the same area.
• Because there are three vertices, there are of course three possible medians.
• No matter what shape the triangle, all three always intersect at a single point. This point is called the centroid of the triangle.
• The three medians divide the triangle into six smaller triangles of equal area.
• The centroid (point where they meet) is the center of gravity of the triangle
• Two-thirds of the length of each median is between the vertex and the centroid, while one-third is between the centroid and the midpoint of the opposite side.
• m=\sqrt{\frac{2b^2+2c^2-a^2}{4}}, where a, b and c are the sides of the triangle and a is the side of the triangle whose midpoint is the extreme point of median m.


Area The number of square units it takes to exactly fill the interior of a triangle.

Usually called "half of base times height", the area of a triangle is given by the formula below.
• A=\frac{hb}{2}

Other formula:
• A=\frac{P*r}{2}

• A=\frac{abc}{4R}

Where b is the length of the base, a and c the other sides; h is the length of the corresponding altitude; R is the Radius of circumscribed circle; r is the radius of inscribed circle; P is the perimeter

• Heron's or Hero's Formula for calculating the area A = \sqrt{s(s-a)(s-b)(s-c)} where a,b,c are the three sides of the triangle and s = \frac{a+b+c}{2} which is the semi perimeter of the triangle.


Perimeter The distance around the triangle. The sum of its sides.

• For a given perimeter equilateral triangle has the largest area.
• For a given area equilateral triangle has the smallest perimeter.


Relationship of the Sides of a Triangle

• The length of any side of a triangle must be larger than the positive difference of the other two sides, but smaller than the sum of the other two sides.


Interior angles The three angles on the inside of the triangle at each vertex.

• The interior angles of a triangle always add up to 180°
• Because the interior angles always add to 180°, every angle must be less than 180°
• The bisectors of the three interior angles meet at a point, called the incenter, which is the center of the incircle of the triangle.


Exterior angles The angle between a side of a triangle and the extension of an adjacent side.


• An exterior angle of a triangle is equal to the sum of the opposite interior angles.
• If the equivalent angle is taken at each vertex, the exterior angles always add to 360° In fact, this is true for any convex polygon, not just triangles.


Midsegment of a Triangle A line segment joining the midpoints of two sides of a triangle


• A triangle has 3 possible midsegments.
• The midsegment is always parallel to the third side of the triangle.
• The midsegment is always half the length of the third side.
• A triangle has three possible midsegments, depending on which pair of sides is initially joined.


Relationship of sides to interior angles in a triangle

• The shortest side is always opposite the smallest interior angle
• The longest side is always opposite the largest interior angle


Angle bisector An angle bisector divides the angle into two angles with equal measures.


• An angle only has one bisector.
• Each point of an angle bisector is equidistant from the sides of the angle.
• The angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment DC is equal to the ratio of the length of side AB to the length of side AC: \frac{BD}{DC}=\frac{AB}{AC}
• The incenter is the point where the angle bisectors intersect. The incenter is also the center of the triangle's incircle - the largest circle that will fit inside the triangle.


Similar Triangles Triangles in which the three angles are identical.

• It is only necessary to determine that two sets of angles are identical in order to conclude that two triangles are similar; the third set will be identical because all of the angles of a triangle always sum to 180º.
• In similar triangles, the sides of the triangles are in some proportion to one another. For example, a triangle with lengths 3, 4, and 5 has the same angle measures as a triangle with lengths 6, 8, and 10. The two triangles are similar, and all of the sides of the larger triangle are twice the size of the corresponding legs on the smaller triangle.
• If two similar triangles have sides in the ratio \frac{x}{y}, then their areas are in the ratio \frac{x^2}{y^2}


Congruence of triangles Two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in size.

1. SAS (Side-Angle-Side): If two pairs of sides of two triangles are equal in length, and the included angles are equal in measurement, then the triangles are congruent.

2. SSS (Side-Side-Side): If three pairs of sides of two triangles are equal in length, then the triangles are congruent.

3. ASA (Angle-Side-Angle): If two pairs of angles of two triangles are equal in measurement, and the included sides are equal in length, then the triangles are congruent.

So, knowing SAS or ASA is sufficient to determine unknown angles or sides.

NOTE IMPORTANT EXCEPTION:
The SSA condition (Side-Side-Angle) which specifies two sides and a non-included angle (also known as ASS, or Angle-Side-Side) does not always prove congruence, even when the equal angles are opposite equal sides.

Specifically, SSA does not prove congruence when the angle is acute and the opposite side is shorter than the known adjacent side but longer than the sine of the angle times the adjacent side. This is the ambiguous case. In all other cases with corresponding equalities, SSA proves congruence.

The SSA condition proves congruence if the angle is obtuse or right. In the case of the right angle (also known as the HL (Hypotenuse-Leg) condition or the RHS (Right-angle-Hypotenuse-Side) condition), we can calculate the third side and fall back on SSS.

To establish congruence, it is also necessary to check that the equal angles are opposite equal sides.

So, knowing two sides and non-included angle is NOT sufficient to calculate unknown side and angles.

Angle-Angle-Angle
AAA (Angle-Angle-Angle) says nothing about the size of the two triangles and hence proves only similarity and not congruence.

So, knowing three angles is NOT sufficient to determine lengths of the sides.


Scalene triangle all sides and angles are different from one another

• All properties mentioned above can be applied to the scalene triangle, if not mentioned the special cases (equilateral, etc)


Equilateral triangle all sides have the same length.


• An equilateral triangle is also a regular polygon with all angles measuring 60°.
• The area is A=a^2*\frac{\sqrt{3}}{4}

• The perimeter is P=3a
• The radius of the circumscribed circle is R=a*\frac{\sqrt{3}}{3}
• The radius of the inscribed circle is r=a*\frac{\sqrt{3}}{6}
• And the altitude is h=a*\frac{\sqrt{3}}{2} (Where a is the length of a side.)
• For any point P within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle.
• For a given perimeter equilateral triangle has the largest area.
• For a given area equilateral triangle has the smallest perimeter.
• With an equilateral triangle, the radius of the incircle is exactly half the radius of the circumcircle.


Isosceles triangle two sides are equal in length.


• An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length.
• For an isosceles triangle with given length of equal sides right triangle (included angle) has the largest area.
• To find the base given the leg and altitude, use the formula: B=2\sqrt{L^2-A^2}

• To find the leg length given the base and altitude, use the formula: L=\sqrt{A^2+(\frac{B}{2})^2}

• To find the altitude given the base and leg, use the formula: A=\sqrt{L^2-(\frac{B}{2})^2} (Where: L is the length of a leg; A is the altitude; B is the length of the base)


Right triangle A triangle where one of its interior angles is a right angle (90 degrees)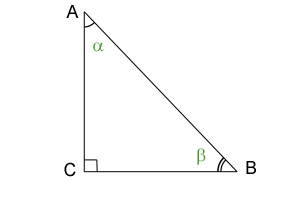


• Hypotenuse: the side opposite the right angle. This will always be the longest side of a right triangle.
• The two sides that are not the hypotenuse. They are the two sides making up the right angle itself.
• Theorem by Pythagoras defines the relationship between the three sides of a right triangle: a^2 + b^2 = c^2, where c is the length of the hypotenuse and a, b are the lengths of the the other two sides.
• In a right triangle, the midpoint of the hypotenuse is equidistant from the three polygon vertices
• A right triangle can also be isosceles if the two sides that include the right angle are equal in length (AB and AC in the figure above)
• Right triangle with a given hypotenuse has the largest area when it's an isosceles triangle.
• A right triangle can never be equilateral, since the hypotenuse (the side opposite the right angle) is always longer than the other two sides.
• Any triangle whose sides are in the ratio 3:4:5 is a right triangle. Such triangles that have their sides in the ratio of whole numbers are called Pythagorean Triples. There are an infinite number of them, and this is just the smallest. If you multiply the sides by any number, the result will still be a right triangle whose sides are in the ratio 3:4:5. For example 6, 8, and 10.
• A Pythagorean triple consists of three positive integers a, b, and c, such that a^2 + b^2 = c^2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. There are 16 primitive Pythagorean triples with c ≤ 100:
(3, 4, 5) (5, 12, 13) (7, 24, 25) (8, 15, 17) (9, 40, 41) (11, 60, 61) (12, 35, 37) (13, 84, 85) (16, 63, 65) (20, 21, 29) (28, 45, 53) (33, 56, 65) (36, 77, 85) (39, 80, 89) (48, 55, 73) (65, 72, 97).


• A right triangle where the angles are 30°, 60°, and 90°.

This is one of the 'standard' triangles you should be able recognize on sight. A fact you should commit to memory is: The sides are always in the ratio 1 : \sqrt{3}: 2.
Notice that the smallest side (1) is opposite the smallest angle (30°), and the longest side (2) is opposite the largest angle (90°).

• A right triangle where the angles are 45°, 45°, and 90°.

This is one of the 'standard' triangles you should be able recognize on sight. A fact you should also commit to memory is: The sides are always in the ratio 1 : 1 : \sqrt{2}. With the \sqrt{2} being the hypotenuse (longest side). This can be derived from Pythagoras' Theorem. Because the base angles are the same (both 45°) the two legs are equal and so the triangle is also isosceles.
• Area of a 45-45-90 triangle. As you see from the figure above, two 45-45-90 triangles together make a square, so the area of one of them is half the area of the square. As a formula A=\frac{S^2}{2}. Where S is the length of either short side.

• Right triangle inscribed in circle: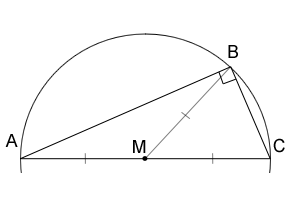

R = \frac{AC}{2}

• If M is the midpoint of the hypotenuse, then BM = \frac{1}{2}AC. One can also say that point B is located on the circle with diameter AC. Conversely, if B is any point of the circle with diameter AC (except A or C themselves) then angle B in triangle ABC is a right angle.
• A right triangle inscribed in a circle must have its hypotenuse as the diameter of the circle. The reverse is also true: if the diameter of the circle is also the triangle’s hypotenuse, then that triangle is a right triangle.

• Circle inscribed in right triangle: r = \frac{ab}{a+b+c}=\frac{a+b-c}{2}

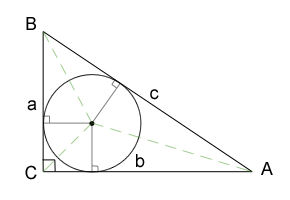
Note that in picture above the right angle is C.

• Given a right triangle, draw the altitude from the right angle.

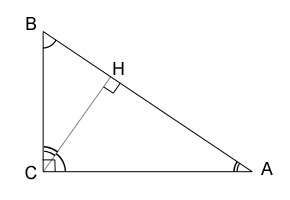
Then the triangles ABC, CHB and CHA are similar. Perpendicular to the hypotenuse will always divide the triangle into two triangles with the same properties as the original triangle.


Official GMAC Books:

The Official Guide, 12th Edition: DT #19; DT #28; PS #48; PS #152; PS #205; PS #209; PS #229; DS #20; DS #56; DS #74; DS #109; DS #140; DS #144; DS #149; DS #157; DS #160; DS #173;
The Official Guide, Quantitative 2th Edition: PS #44; PS #71; PS #85; PS #145; PS #157; PS #162; DS #19; DS #65; DS #88; DS #91; DS #123;
The Official Guide, 11th Edition: DT #19; DT #28; PS #45; PS #152; PS #158; PS #226; PS #248; DS #27; DS #32; DS #51; DS #66; DS #108; DS #113; DS #124; DS #136; DS #152;

Generated from [GMAT ToolKit]


--------------------------------------------------------

Thank you very much for spotting the typos. +1.

Quite a long post so no wonder I missed some of them. I'll try to avoid them in the future.

BTW if someone has any other properties of triangles, which might be useful for GMAT, he/she can post here and I'll add them to the original post.



Sorry, I don't even know which resource you are referring to. These properties are form various sources: GMAT problems, geometry sites, etc.

Wow Bunuel... You never cease to amaze me!

Great Post. Really enjoyed going through it. Cant imagine how much time and effort it must have taken you to compile and format it.

Kudos to you.


Ps. Noticed a couple of typos you might've overlooked.



The formula should be m=\sqrt{\frac{2b^2+2c^2-a^2}{4}} where m is the length of the median.




The radius of the circumscribed circle for an equilateral triangle should be : R=a*\frac{\sqrt{3}}{3}


Also, was just wondering, since you have included a number of formulae for calculating area of a triangle, might as well include this one : A = \sqrt{s(s-a)(s-b)(s-c)} where a,b,c are the three sides of the triangle and s = \frac{a+b+c}{2} which is the semi perimeter of the triangle.

Once again.. Great post.

Keep 'em coming!

Cheers.

Wow!!! +1 - really good.

Exceptional... a really well compiled data on triangles and their properties...
the best part was to mention the problems from the official GMAT books.... +2

i think it would be worth mentioning the sine and cosine rules of triangles...

The law of sines (or Sine Rule):

If A, B and C are the angles made by the sides a= BC, b= CA & c= AB at the vertices of a triangle ABC, then according to the sine rule, (a/sin A) = (b/sin B) = (c/sin C)

The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known.

The law of cosines (or Cosine Rule) :

If A, B and C are the angles made by the sides a= BC, b= CA & c= AB at the vertices of a triangle ABC, then according to the cosine rule,

a^2 = b^2 + c^2 - 2bc(cos A); b^2 = a^2 + c^2 - 2ac(cos B); c^2 = a^2 + b^2 + 2ab(cos C)

The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known, and in computing the angles of a triangle if all three sides are known.

hello Bunuel you said:

To find the leg length given the base and altitude, use the formula: A=\sqrt{L^2-(\frac{B}{2})^2} i believe you were supposed to say Altitude instead. ? right?

my question: is there specific formula for isosceles Area? somebody mentioned but i was no able to find the one.
thanks

First of all: do not fully quote such big texts. Do as I edited know: quote only the specific part you are referring to.

Next, formula indicates Altitude=... so yes there was a typo. Thanks for spotting. Edited.

As for your question: you won't need any other formula for the area of an isosceles triangle but area=1/2*base*height. The are of isosceles right triangle is area=leg^2/2.

kudos!!!!

Woo!! Woo! Woo!!

So here comes our master, to theoretical posts

God bless you!!

Wonderful team, wonderful site. +2

Bunuel, You Rock!!!!
+10.

WWWWWWWWWOOOOOW ++++

I totally needed this.

sriharimurthy, Bunuel,

All of this is from S Chand Intermediate First year Mathematics Textbook, Andhra Pradesh Intermediate Public Examination Board, India?

As always Awesome post Bunuel!!!! Many Kudos. You have taken this forum to a new level. Thank you very much for your time and efforts.

Excellent job!!!

+1

touche, great post !~!

awesome work

Bunuel

might I suggest you to create another post with subject: "All you want to know about Quantitative" and provide links to your various posts in it? That way we all can bookmark just one page and still can have all the information from you? Also in this way if you add any new post, we will not miss it.

You might also want to create a master thread containing links to all your posts of different sets of problems. That weay we can have a central repository to different types of problems eg. Inequality, Combinatorics, etc.

This will help a lot .. another thanks ..

I wish somebody made a pdf compilation of Bunuel's posts...