I have explained the concept below from which we derive the following formula. It makes calculations very simple and you don't need to learn up the formula because it will make sense and stick with you once you go through the explanation:
\(( 1 + \frac{m}{100}) * (1 - \frac{d}{100}) = (1 + \frac{p}{100})\)
where m% is mark up %, d% is discount % and p% is profit %.
Using the formula to solve your question:
If d = 20 and p = 20,
\(( 1 + \frac{m}{100}) * (1 - \frac{20}{100}) = (1 + \frac{20}{100})\)
\(( 1 + \frac{m}{100}) * (\frac{4}{5}) = (\frac{6}{5})\)
m = 50
Therefore, the merchant had marked up by 50% which would have been his profit had he not given the discount.
Let me explain the concept now.
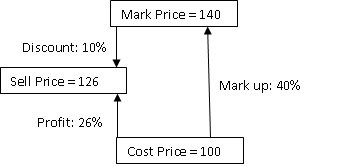
Let us say cost price of an item is $100. I, a merchant, mark it up by 40% and put a tag on it of $140. Now, I have a sale and I offer everything at 10% discount. So something that is marked at $140, will get $14 off and will be sold at $126. The profit I made on the item is $26 (= 126 - 100 (which was my cost price)). This profit is equal to a profit % of 26/100 = 26% (Profit/CP x 100)
Note here that my mark up % was 40%, I gave discount of 10% but my profit is only 26%, not 30%. This is because the 40% mark up was on cost price while when I gave discount, I gave 10% on the marked price (which was way more than cost price). The diagram below will make this clearer.
Attachment:
 Ques.jpg [ 13.44 KiB | Viewed 261688 times ]
Ques.jpg [ 13.44 KiB | Viewed 261688 times ]
We can make up a quick formula.
If m% is the mark up %, d% is the discount % and p% is the profit %, then
cost price x ( 1 + m/100) = marked price
marked price x (1 - d/100) = selling price
which means: cost price x ( 1 + m/100) x (1 - d/100) = selling price
We know, cost price x (1 + p/100) = selling price
From the 2 equations above, \(( 1 + \frac{m}{100}) * (1 - \frac{d}{100}) = (1 + \frac{p}{100})\)
In other words, when cost price is increased by m% and then decreased by d%, it is equivalent to increasing the cost price by p%.



 45%
(medium)
45%
(medium)
 28%
(02:27)
wrong
28%
(02:27)
wrong  based on 2397
sessions
based on 2397
sessions






