violetsplash wrote:
A survey was conducted to determine the popularity of 3 foods among students. The data collected from 75 students are summarized as below
48 like Pizza
45 like Hoagies
58 like tacos
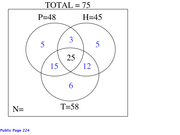
28 like pizza and hoagies
37 like hoagies and tacos
40 like pizza and tacos
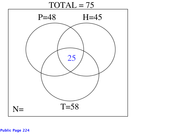
25 like all three food
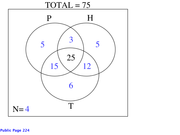
What is the number of students who like none or only one of the foods ?
A. 4
B. 16
C. 17
D. 20
E. 23
I got this one right but I spent a lot of time playing with numbers. Can someone please show a faster way.
So it turns out this question doesn't need the whole method that Harry from GMAT Ninja taught (the better Harry

), so if you want to see the whole method, you can find it here:
https://youtu.be/FJa6Dz5p1Ko?t=23573Using the table he suggests, this question becomes very simple. Absolutely watch the video linked above (and if you can, please do support the cause they were fundraising for).
To sum up their method, I'd break it down into a few steps:
1a. Identify
how many groups you have, with memberships that are overlapping (e.g., in this case, the number of foods liked by any individual).
1b.
Label a column "# groups" with the word groups replaced with whatever title is appropriate.
1c.
Fill in the numbers for the groups with the information you know from the question.
2a. Make a
second column for the
number of members (e.g., in this case, the # of students)
2b.
Fill in this column with the information you have from the question.
Add a total row for the total number of members and fill it in if we know it.
2c.
If the question is asking for one of these numbers, mark it with "X", as this will be the number we build the table around to solve for.
In this question, you don't need step 3, but I'll include it for completeness.3a. Make a
third column for the
number of memberships including overlaps (e.g., in this case, every food that is liked by every individual).
Note: This number will be greater than the total number of people because by definition some people are members of more than one group (e.g., like more than one food).3b. Fill in this column with any information we know from the question.
If the question is asking for one of these numbers, mark it with "X", as this will be the number we build the table around to solve for.
Note: We may need to sum the total memberships to find the value for the total row here (e.g., 48 like Pizza + 45 like Hoagies + 58 like tacos).
4. Any empty spaces, fill them in by
creating expressions using the numbers around them and X.
Solve for X.
So my summary of Steps 1, 2, and 4 to solve this is in this table:

So the
answer is D, as there are 20 people who like either 0 or 1 food.
Just FYI, if the question required it, possible values for Column 3 (Overlaps) could have been:(X * 0) + Y
60 = 2 foods * 30 members
75 = 3 foods * 25 members
---
151
GMATNinja wrote:
Vubar wrote:
GMATNinja Just wanted to check, how would you feel about me sharing the method you (Harry) taught during the 24-hour stream, for tackling this question?
Thank you so much for asking,
Vubar! Since we shared it publicly in a video, it's absolutely no problem to post it here, especially if it includes a shoutout to Harry.

And thank you for sticking with the whole marathon,
Vubar! It meant a lot to me.
Thank you Charles! And thank you again, and everyone who helped organise, for making it happen. Trying to help spread the word was the least I could do. I did delay my exam date though, trying to recover the sleep - I am sure you will understand better than most!