A bus from city M is traveling to city N at a constant speed while another bus is making the same journey in the opposite direction at the same constant speed. They meet in point P after driving for 2 hours. The following day the buses do the return trip at the same constant speed. One bus is delayed 24 minutes and the other leaves 36 minutes earlier. If they meet 24 miles from point P, what is the distance between the two cities?let d=distance (what the question is looking for)
On the first day, bus a and bus b travel at the same constant speed. Because they travel at the same constant speed, when they meet at point P they have each traveled for 2 hours. Therefore, the total time (at that constant speed) from A to B is 4 hours and P is the mid distance between those two points.
On the second day each bus travels at the same constant speed. The bus that leaves first spends a total of one hour on the road before the second bus leaves (if bus a and bus b normally leave at the same time and today one leaves 36 minutes earlier and 24 minutes later respectively)
Here is where I get thrown off (using Bunuel's explanation to structure mine)The wording is a bit ambiguous (at least to me) regarding the constant speed of bus A and bus B. On the second day, do they travel the same constant speed they did the day before or did they each travel the same constant speed that day that is different from the day before?If they each traveled at the same rate they did before (which is 1/4 of the distance every hour) and today one bus traveled for an hour before the other set off, then today one bus traveled .25d of the way
(d/2) - 24 = (.75d/2)
(I'm not sure as to why that is)Maybe this is why:
(d/2) represents the speed each bus travels and the midpoint at which bus A and B meet on the first day. (d/2)-24 would represent the bus reaching a point 24 miles before the midpoint. This is equal to a distance that's 3/4ths normal????
Help!!! Bunuel, I read the link you posted offering an explanation of how that formula represents the point at which each bus meets the second day but I am still confused. Why is the halfway .75d?
Here is another way to look at it. Let's say bus A starts first and B, second. When bus A travels one hour bus B starts. When bus A has traveled for two hours, bus B has traveled for one. When bus A and B meet, A has been on the road for 2.5 hours and B, for 1.5 at a place 24 miles away from the mid distance of the journey.
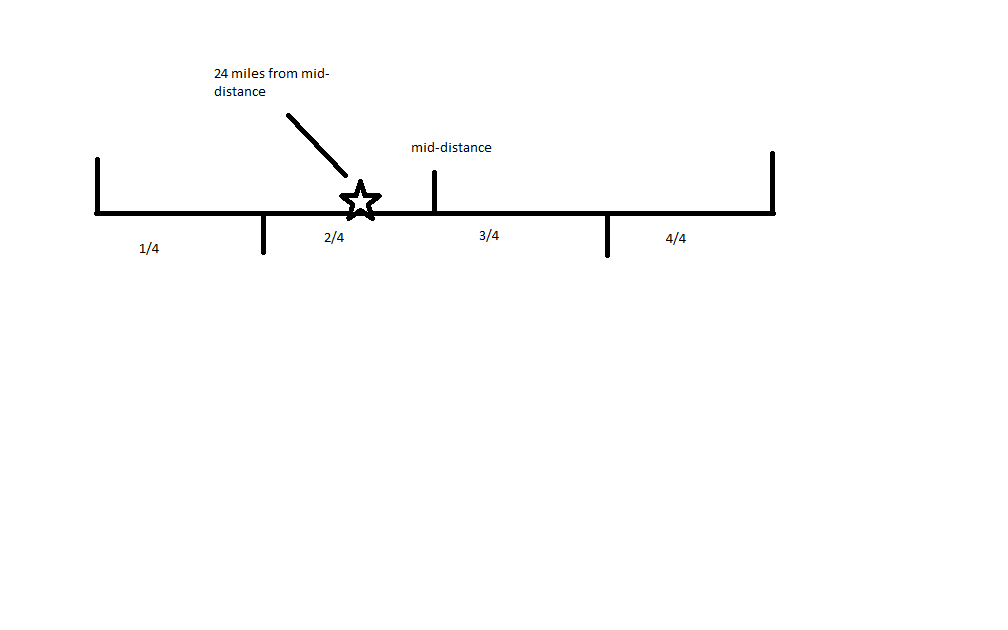
We can break the journey up into four identical blocks, each representing an hour long portion of the journey (see attached image) when bus A and B meet they meet in the exact middle of one of those 4 identical blocks meaning that 24 miles represents 1/2 of one block. This means there are two 24 mile portions in each of the four blocks. 2*24*4=192.
A. 48
B. 72
C. 96
D. 120
E. 192
Attachments
Untitled.png [ 6.98 KiB | Viewed 36619 times ]



 95%
(hard)
95%
(hard)
 71%
(03:00)
wrong
71%
(03:00)
wrong  based on 1814
sessions
based on 1814
sessions







