If x, y and z are positive integers such that x^4*y^3 = z^2

Detailed Solution

Step-I: Given Info

We are given three positive integers \(x\), \(y\) and \(z\) such that \(x^4y^3 = z^2\), and we are asked to find if \(x^9 – y^6\) is odd

Step-II: Interpreting the Question Statement

For the expression \(x^9 – y^6\) to be odd, both the expressions need to be of opposite even/odd nature i.e. one has to be odd and another has to be even (as even- odd = odd or odd-even = odd). Since the even/odd nature of \(x^9\) would have the same even/odd nature as \(x\) and even/odd nature of \(y^6\) would be the same even/odd nature as \(y\), if we can determine the similar or opposite nature of \(x\) , \(y\) we can determine the even/odd nature of \(x^9 – y^6\).

Step-III: Statement-I

We are told that \(\frac{x^4y^3}{x^2 + y^2}\) can be written in the form \(4k + 3\), where \(k\) is a positive integer. We observe here that a fraction has been simplified to an odd number (as \(4k\) is always even and even + odd = odd) which would imply that both the numerator and the denominator are either even or odd.
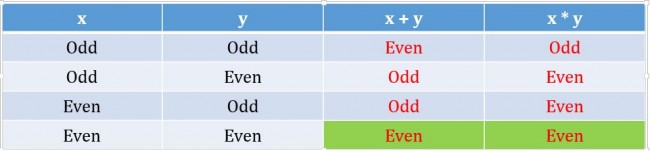
Hence, we can say that the product of \(x\) and \(y\) and the sum of \(x\) and \(y\) have the same even/odd nature.

This is possible only if \(x\), \(y\) are both even. Since, we have determined the similar nature of \(x\), \(y\) we can say with certainty that expression \(x^9 – y^6\) is always even.
Hence, statement-I is sufficient to answer the question.

Step-IV: Statement-II

Statement-II tells us that \(z = x + y\), we know that \(z\) is expressed as a product of \(x\) and \(y\). Since the product of \(x\), \(y\) have the same even/odd nature as that of the sum of \(x\) and \(y\), we can say with certainty that \(x\), \(y\) are both even.
Hence, statement-II is sufficient to answer the question.

Step-V: Combining Statements I & II

Since, we have a unique answer from Statement- I & II we don’t need to be combine Statements- I & II.
Hence, the correct answer is Option D

Key Takeaways

1. In even-odd questions, simplify complex expressions into simpler expressions using the properties of even-odd combinations.
2. Know the properties of Even-Odd combinations to save the time spent deriving them in the test
3. The even/odd nature of some expressions can be determined without knowing the exact even/odd nature of the variables of the expressions by using the even/odd combination property

Harley1980- Great Job!
shuvabrata88- You missed out on the analysis of St-I where even/odd nature of a fraction was to be analyzed.

Regards
Harsh