M16-15

Official Solution:


Approach 1:

If the vertices of a triangle have coordinates \((-1, 0)\), \((4, 0)\), and \((0, A)\), is the area of the triangle greater than 15?

(1) \(A \lt 3\)

Statement (1) alone is insufficient. If \(A\) is close to 0, the area of the triangle is small, but if \(A\) is a large negative number (for example, \(A = -1000\)), the area of the triangle is large.

(2) The triangle is a right triangle

Statement (2) alone is sufficient. Only the angle at vertex \((0, A)\) can be a right angle. As \(|A|\) increases, the value of the angle decreases. At some point, the angle becomes equal to 90 degrees, and we can snapshot the triangle at this moment. After that, we can find the area of the triangle and answer the question. Please see the image below.



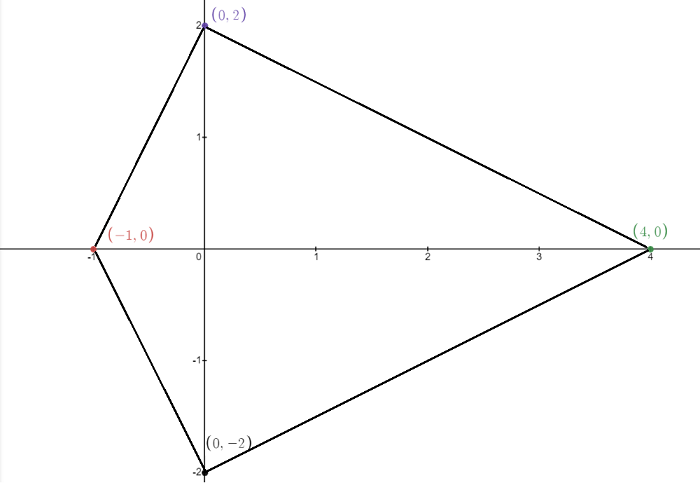
Approach 2:

If the vertices of a triangle have coordinates \((-1, 0)\), \((4, 0)\), and \((0, A)\), is the area of the triangle greater than 15?

(1) \(A \lt 3\)

Two vertices lie on the x-axis, and the third vertex is on the y-axis, below the point (0, 3). The third vertex could be at (0, 1), resulting in an area less than 15, OR the third vertex could be at (0, -100), resulting in an area greater than 15. Therefore, this statement alone is not sufficient.

(2) The triangle is a right triangle

It is evident that the third vertex, which is located on the y-axis, forms a right angle. Consequently, the hypotenuse, which is on the x-axis, measures 5 units. We can consider this hypotenuse as the diameter of a circle as shown below:



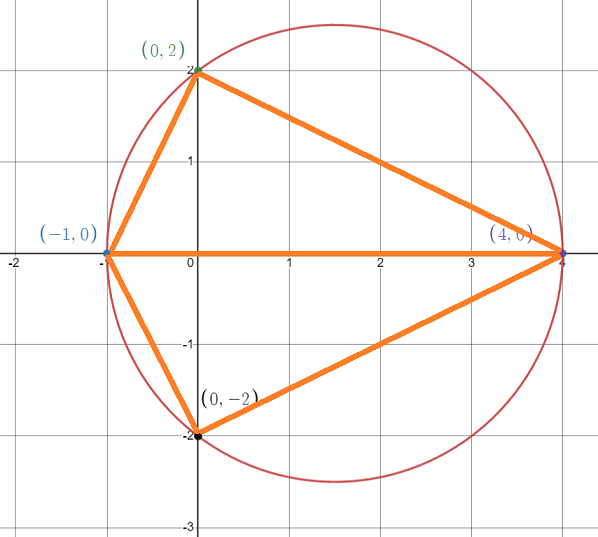
Any point on the circumference of that circle will create a right angle with the diameter/hypotenuse. This is because a right triangle inscribed in a circle must have its hypotenuse as the diameter of the circle. Conversely, if the diameter of the circle is also the triangle's hypotenuse, then that triangle is a right triangle.

Since we know that the third vertex is on the y-axis, it must be one of the two intersection points of the circle with the y-axis. Thus, we obtain two symmetrical triangles with equal areas. Both of these triangles are fixed and defined, allowing us to determine whether their area is greater than 15 without calculating the exact value. Therefore, this statement alone is sufficient.

If we wish to understand how the area can be calculated with the help of statement 2, here is an explanation:

One approach is to use the equation of a circle: \((x - a)^2 + (y - b)^2 = r^2\), where \((a, b)\) represents the center and \(r\) represents the radius.

In this case, we know that \(r = 2.5\) because the hypotenuse measures 5 units. The center of the circle, denoted by \((a, b)\), lies on the x-axis at the point \((1.5, 0)\), which is halfway between (-1, 0) and (4, 0).

To find the intersection points of the circle with the y-axis, we need to determine the y-coordinate \(y\) when \(x = 0\). Substituting these values into the equation of the circle, we have:

\((0 - 1.5)^2 + (y - 0)^2 = 2.5^2\).

Simplifying, we get \(y^2 = 4\), which yields two possible values for \(y\): \(y = 2\) and \(y = -2\). Consequently, the third vertex can be located at either (0, 2) or (0, -2). In either case, the area can be calculated using the formula \(Area = \frac{1}{2}*\text{base }*\text{height}\). Plugging in the values, we have \(Area = \frac{1}{2}*5*2 = 5\).

Therefore, the area of the triangle is 5, which is less than 15.


Answer: B