[GMAT math practice question]
(geometry)
Attachment:
 8.16 DS.png [ 12.5 KiB | Viewed 1518 times ]
8.16 DS.png [ 12.5 KiB | Viewed 1518 times ]
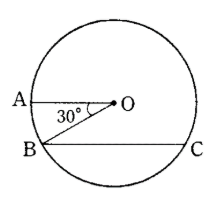
In the figure, ∠AOB= 30°. What the length of arc BC?
1) AO is parallel to BC
2) the length of arc AB is 5
=>
Forget conventional ways of solving math questions. For DS problems, the VA (Variable Approach) method is the quickest and easiest way to find the answer without actually solving the problem. Remember that equal numbers of variables and independent equations ensure a solution.
In order to determine BC, we need to know the radius of the circle and the measure of angle <BOC. Thus, we have 2 variables and 0 equations, and C is most likely to be the answer. So, we should consider conditions 1) & 2) together first. After comparing the number of variables and the number of equations, we can save time by considering conditions 1) & 2) together first.
Conditions 1) & 2)
Since AO and BC are parallel, <OBC = 30° (alternate interior angles).
Since OB and OC are congruent (equal radii), <OCB 30°.
Thus <BOC = 180°-30°-30°=120°
The ratio between the arc lengths of AB and BC is 30:120 = 1:4.
Thus, the arc length of BC is 4 times the arc length of AB, so it is 20.
Both conditions together are sufficient.
Note: condition 1) cannot be sufficient as it provides no information about the radius of the circle.
Therefore, the answer is C.
Answer: C
Normally, in problems which require 2 equations, such as those in which the original conditions include 2 variables, or 3 variables and 1 equation, or 4 variables and 2 equations, each of conditions 1) and 2) provide an additional equation. In these problems, the two key possibilities are that C is the answer (with probability 70%), and E is the answer (with probability 25%). Thus, there is only a 5% chance that A, B or D is the answer. This occurs in common mistake types 3 and 4. Since C (both conditions together are sufficient) is the most likely answer, we save time by first checking whether conditions 1) and 2) are sufficient, when taken together. Obviously, there may be cases in which the answer is A, B, D or E, but if conditions 1) and 2) are NOT sufficient when taken together, the answer must be E.

