alphabeta1234 wrote:
I have an equation that looks like this |x – 3| + |x + 1| + |x| = 10 and I want to find the x that satisfies the condition.
I know that -1,0, and 3 are my pivot points that I have to test.
x<-1
-1<=x<=0
0<x<=3
Knowing these are the three ranges where the function changes values is there a quick way to evaluate each subcomponent and know whether it will be positive or negative within that range? I always get stuck on this point because I have to evaluate every subcomponent and figure out what sign i takes with in that range.
For example, in the x<-1 range is each subcomponent evaluates too:
|x-3|=-(x-3) (because |x-3|=-(x-3) if x-3<0, ie, x<3. Because our range is x<-1, clearly within the range of x<3, we place a negative sign)
|x+1|=-(x+1)
and |x|=-x
Just trying to find a quicker way without checking the inequalities to know if I should place a (-) sign on the subcomponents or not.
We know that |x-0| is the distance of the point x from the origin. Representing all the pivotal points on the number line, the question finally boils down to this : For What value(s) of x, will the distance of x from the points -1,0 and 3 add upto to give 10 units?
Attachment:
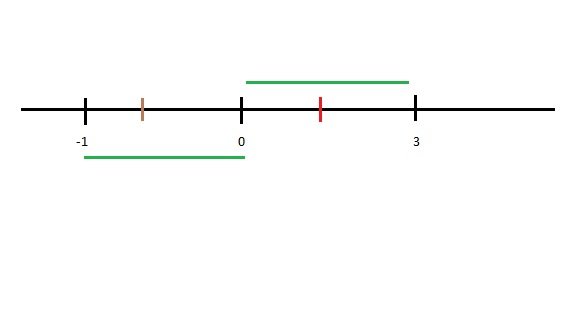 Image.jpg [ 8.44 KiB | Viewed 1678 times ]
Image.jpg [ 8.44 KiB | Viewed 1678 times ]
I. \(0
<=x
<=3\) Note that for any x,the expression |x|+|x-3| will always give you a CONSTANT sum of distance as 3 units only, i.e. |x|+|x-3| = 3. Also, assuming x to be farthest in this range i.e. at x= 3, the distance between x = 3 and x = -1 is 4 units. Thus, the sum total of all the distances,i.e.
|x – 3| + |x + 1| + |x| is at most 7 units.Thus, no x for [0,3] will ever add upto 10, for the above mentioned expression.
II. \(-1=
<x
<=0\) Note the expression |x|+|x+1| will always give you a CONSTANT sum of distance as 1 unit only , i.e. |x|+|x+1| = 1. Again, just as above, assuming x to be farthest in the range i.e. at x = -1, the distance between x = -1 and x = 3 is 4 units. Thus, the sum total of all the distances,i.e.
|x – 3| + |x + 1| + |x| is at most 5 units.Thus, no x for [-1,0] will ever add upto 10, for the above mentioned expression.
III. For \(x>3\) Notice that we have already found out that the maximum sum of distance for x = 3 is 7 units.Now, if i take any value of x>3, it would give a value which is more than 7 units;so now, we know that THERE IS one unique value of x for this range, which will give the sum of distance as 10 units.Thus, we need an extra 3 units. To find the exact value of x, note that the extra 3 units will be contributed by each of the 3 points (-1,0 and 3) EQUALLY, i.e. 1 unit from each of the 3 pivotal points. Thus, as x gets a distance of 1 unit from 3, hence x = 3+1 = 4. Thus, x = 4 is one solution.
II.For \(x<-1\) Notice that we have already found the maximum sum of distance for x = -1 is 5 units.As per the problem, this total should be 10 units. Thus, we need an extra 5 units.Just as above, we know for sure that THERE IS another unique value of x, which will give a sum total of 10 units. To find the exact value of x, note that the extra 5 units will be contributed by each of the 3 points (-1,0 and 3) EQUALLY. Thus, as x is at a distance of \(\frac{5}{3}\) unit from -1 and also x<-1, hence x = \(\frac{-8}{3}\).
Hope this helps.

