Events & Promotions
| Last visit was: 26 Apr 2024, 02:27 |
It is currently 26 Apr 2024, 02:27 |

Customized
for You
Track
Your Progress
Practice
Pays
12:00 PM EDT
-01:00 PM EDT
03:00 PM PDT
-04:00 PM PDT
01:00 PM EDT
-11:59 PM EDT
11:00 AM EDT
-12:00 PM EDT
11:00 AM IST
-01:00 PM IST
08:00 PM PDT
-09:00 PM PDT
05:30 AM PDT
-07:30 AM PDT
11:00 AM IST
-01:00 PM IST
12:00 PM PDT
-01:00 PM PDT
12:00 PM EDT
-01:00 PM EDT
Difficulty:


 55%
(hard)
55%
(hard)
Question Stats:
61% (01:37) correct 39%
(02:01)
wrong
39%
(02:01)
wrong  based on 337
sessions
based on 337
sessions
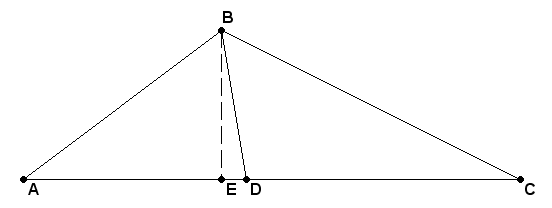


|
|
||
|
Hi Generic [Bot],
Here are updates for you:
ANNOUNCEMENTS
Watch earlier episodes of DI series below EP1: 6 Hardest Two-Part Analysis Questions EP2: 5 Hardest Graphical Interpretation Questions
Tuck at Dartmouth
|