Bunuel wrote:
voodoochild wrote:
walker wrote:
Area of a rectangle ranges from 0 to area of square=2. S0, I and II is possible.
Bunuel / Walker,
I have a question. If the diameter = 2 => diagonal of square =2 => 2(side of a square)^2 =
2 =>
(side of a square)^2 = 1.
Hence,
the area of square is 1! Thoughts?
If the length of a diagonal of a square is 2, then
side^2+side^2= diagonal^2 -->
2*side^2=2^2 -->
side^2=area=2.
You could get the side in another way: since the angle between a diagonal and a side in a square is 45 degrees, then
side=\frac{diagonal}{\sqrt{2}} (from the properties of 45-45-90 triangle).
You could also get the area directly:
area_{square}=\frac{diagonal^2}{2}=2.
Complete solution:
A rectangle is inscribed in a circle of diameter 2. Which of the following can be the area of the rectangle?I. 0.01
II. 2.00
III. 3.20
A. I only
B. II only
C. III only
D. I and II only
E. II and III only
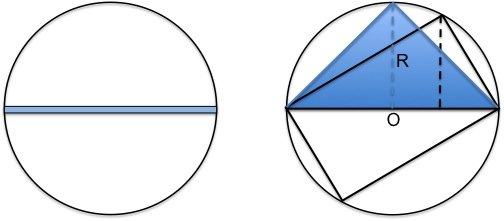
Look at the diagram below:
If the width of blue rectangle is small enough then its area could be 0.01.
Generally,
the are of the inscribed rectangle is more than 0 and less than or equal to the area of the inscribed square (inscribed square has the largest area from all rectangles that can be inscribed in a given circle).
Now, since the area of the inscribed square in a circle with the diameter of 2 is 2, then the area of the inscribed rectangle is
0<area\leq{2}. So, I and II are possible values of the area. (Else you can notice that the area of the circle is
\pi{r^2}=\pi\approx{3.14} and the area of the inscribed rectangle cannot be greater than that, so III is not possible)
Answer: D.
The link to the figure is not working/missing...
Did you mean something like this? (See the attached figure)
We can make the area of the inscribed rectangle as close as possible to 0, when for example the length is getting closer, and closer to the diameter, while the width is getting closer and closer to 0.
The maximum area can be obtained when the height of the right triangle, which is half of the rectangle and it is inscribed in the half circle, is equal to the radius of the circle. In this case, the rectangle becomes a square.
Attachments
MAxRectangleAreaInCircle.jpg [ 24.29 KiB | Viewed 1107 times ]
_________________
PhD in Applied Mathematics
Love GMAT Quant questions and running.
close
45% (01:24) correct
)
<sad> Thanks again.
