mniyer wrote:
Hi,
Is it possible to find the vertices of a straight line with the following information?
1) we know the equation of the line
2) we know the length of the line
3) we know the mid-point of the line
For eg: Is it possible to find the end-points of the line?
1) \(y = \frac{3}{2}x - \frac{1}{2}\)
2) length = \(\sqrt{52}\)
3) mid point of the line is (3,4)
You don't have end points of a line. A line extends indefinitely in both directions. You have end points of a line segment.
And yes, you can easily find the end point co-ordinates. But before you do, you need to understand a few things.
The equation of a line is given as y = mx + c
m is the slope of the line. The slope means the change in y coordinate for a unit change in x coordinate. The equation of the line here is y = (3/2)x - 1/2. So for every 1 unit increase in x coordinate, y increases by 1.5 units. Similarly for every 1 unit decrease in x coordinate, y decreases by 1.5 units.
Now, according to the given information, this is what the line segment looks like:
Attachment:
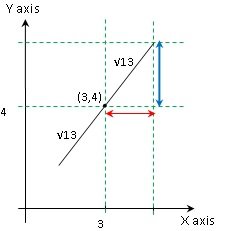 Ques3.jpg [ 11.38 KiB | Viewed 2366 times ]
Ques3.jpg [ 11.38 KiB | Viewed 2366 times ]
Since the length of the line segment is \(\sqrt{52}\), it must be \(\sqrt{52}/2 = \sqrt{13}\) on both sides of the mid point.
Now we need the length of the red arrow and blue arrow to get the coordinates. Since the slope of the line segment is 1.5, it means y coordinate changes by 3 units for every change of 2 units in x coordinate (got rid of the decimal). So length of blue line:length of red line = 3:2
Using pythagorean theorem, \((3a)^2 + (2a)^2 = \sqrt{13}^2\)
a = 1 or -1
So length of blue line is 3 units and length of red line is 2 units.
We obtain the coordinates as (3+2, 4+3) and (3 - 2, 4-3) i.e. (5, 7) and (1, 1)





