Events & Promotions
| Last visit was: 25 Apr 2024, 18:03 |
It is currently 25 Apr 2024, 18:03 |

Customized
for You
Track
Your Progress
Practice
Pays
12:00 PM EDT
-01:00 PM EDT
03:00 PM PDT
-04:00 PM PDT
01:00 PM EDT
-11:59 PM EDT
10:00 AM PDT
-11:00 AM PDT
11:00 AM EDT
-12:00 PM EDT
11:00 AM IST
-01:00 PM IST
11:00 AM IST
-01:00 PM IST
12:00 PM PDT
-01:00 PM PDT
12:00 PM EDT
-01:00 PM EDT
Difficulty:


 95%
(hard)
95%
(hard)
Question Stats:
47% (02:20) correct 53%
(02:07)
wrong
53%
(02:07)
wrong  based on 307
sessions
based on 307
sessions

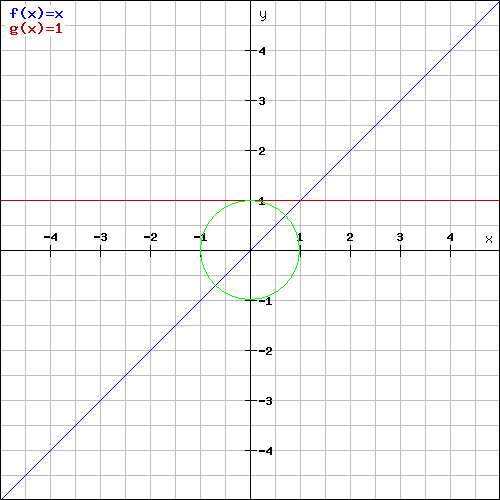


radius.jpg [ 8.85 KiB | Viewed 13650 times ]



|
|
||
|
Hi Generic [Bot],
Here are updates for you:
ANNOUNCEMENTS
Watch earlier episodes of DI series below EP1: 6 Hardest Two-Part Analysis Questions EP2: 5 Hardest Graphical Interpretation Questions
Tuck at Dartmouth
GMAT Club REWARDS
|