ugo_castelo wrote:
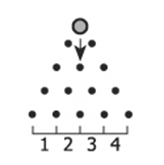
The figure shown represents a board with 4 rows of pegs, and at the bottom of the board are 4 cells numbered 1 to 4. Whenever the ball shown passes through the opening between two adjacent pegs in the same row, it will hit the peg directly beneath the opening. The ball then has the probability 1/2 of passing through the opening immediately to the left of that peg and probability 1/2 of passing through the opening immediately to the right. What is the probability that when the ball passes through the first two pegs at the top it will end in Cell 2?
A. 1/16
B. 1/8
C. 1/4
D. 3/8
E. 1/2
At first here's a takeaway for you:
if you see a probability problem in which it's clear that there are relatively few possibilities, then, unless you IMMEDIATELY see a theoretical approach, you should open the problem by LISTING POSSIBILITIES.whenever you make such a list, the list must of course be organized; if you make a haphazard list of possibilities as they randomly come into your head, with no organizing principle, then you will probably not assemble a complete list (and/or you will accidentally count possibilities more than one time each).
in this case, the ball goes either left or right whenever it hits a peg. this will happen three times between the release and the end of the trajectory, so you have a combination of three L's/R's.
here's an organized list, arranged by increasing numbers of L's (starting with no L's at all, working up to three L's):
LLL
LLR LRL RLL
LRR RLR RRL
RRR
here's another list, arranged alphabetically:
LLL
LLR
LRL
LRR
RLL
RLR
RRL
RRR
either way, you come to the conclusion that there are 8 possibilities, meaning that your probability fraction starts out with a denominator of 8. this is enough to eliminate choice (a), whose denominator is larger than 8, but that's about it.
now, the numerator.
this is the number of possibilities that actually get you into the desired slot.
an examination of the picture reveals that, to get into the desired slot #2, you have to go left exactly 2 times, and right exactly once, in some order. there are three possibilities in the above list that do this: LLR, LRL, and RLL.
therefore, probability = 3 out of 8.
--
THEORY APPROACH:if you didn't think of this in about 15 seconds, then don't continue to look for it; it's here for your edification only. YOU SHOULD NOT KEEP LOOKING FOR THESE SORTS OF THINGS IF YOU DON'T FIND THEM RIGHT AWAY.
REMEMBER THAT YOU SHOULD START LISTING RIGHT AWAY IF YOU DO NOT _IMMEDIATELY_ SEE THE THEORY APPROACH, AS THERE ARE NO POINTS FOR ELEGANCE OR STYLE.the total number of possibilities is the total number of ways to have three L's or R's.
that's three decisions, with two options (L and R) at each decision.
therefore, the total number of possibilities is 2 x 2 x 2, or 8.
the total number of successes is the total number of ways to have two L's out of three.
this is a combination problem; the number of ways of picking two out of three is 3! / (2!1!), or 3.
alternatively, it's the total number of ways to pick one R out of three, which is clearly 3.
either way, 3 out of 8.
Answer is (D).




 95%
(hard)
95%
(hard)
 51%
(02:20)
wrong
51%
(02:20)
wrong  based on 1497
sessions
based on 1497
sessions



