On the number line shown, is zero halfway between r and s ?

Hi Bunuel,

Got this question incorrect on GMAT prep test and thus looked at your solution....

Initially, I tried to do the question by myself and here is what I did

The Question basically asks us whether 0 is between r and s or |r-0|=|s-0| or |r|=|s| or r= s or -s
(Now, if r=s then answer is no but if r=-s then answer is yes...But I think I did apply the mod statement correctly so in this case do we reject the case of r=s at this stage itself and reduce the question to if r=-s )
St 1 says s>0 not much help here as r can be placed to the right of zero or left or at zero. Not sufficient
St 2 says |t-r|=|t+s|
This can be interpreted in one of the 2 ways

t-r = t+s or t-r= -(t+s)

So we get either r=-s or 2t=r+s

Not sufficient.

combining we see that r=-s and s>0 therefore r<0 and r=-s which is same

VeritasKarishma

Can't we say statement 2 is sufficient
by saying that distance between t & r is same as Dist. between t & -s. so we can conclude that -s is at position of r. therefore if -s=r then s is at right side of 0 and r is at left side of 0;so we can say that 0 is halfway of r and s like
-1---0---1.
please explain where i'm faultering.

On the number line shown, is zero halfway between r and s?

(1) s is to the right of zero
(2) The distance between t and r is the same as the distance between t and -s

Solution:

We need to determine whether zero halfway between r and s. We see that 0 could be in one of the following four places: 1) to the left of r, 2) between r and s, 3) between s and t, 4) to the right of t. We will refer to these four cases as cases 1, 2, 3 and 4, respectively.

Statement One Only:

s is to the right of zero.

This tells us s is positive; however, without knowing anything about r, we can’t determine whether they are opposites. Statement one is not sufficient to answer the question.

Statement Two Only:

The distance between t and r is the same as the distance between t and -s.

We see that it can’t be case 1 or 3 since the former case has t further away from -s than it’s from r whereas the latter case has t further away from r than it’s from s. However, it can still be either case 2 or 4. If it’s the former, then yes, not only 0 is between r and s, 0 is exactly halfway between r and s. However, if it’s the latter, then no, because both r and s are less than 0. Statement two is not sufficient to answer the question.

Statements One and Two Together:

From statement two, we know it’s either case 2 or 4. However, since from statement one, s is positive, then it must be case 2 (since this case has s positive) and not case 4 (since this case has s negative). From the analysis for statement two, we see that if it is case 2, then 0 is exactly halfway between r and s. The two statements together are sufficient to answer the question.

Answer: C

How do we know that zero is half way between r and s? You just mentioned that it is between r and s but do we know it is a midpoint?

On the number line shown, is zero halfway between r and s?

(1) s is to the right of zero
(2) The distance between t and r is the same as the distance between t and -s

Let me clear this one:

NOTE:
In GMAT we can often see such statement: \(k\) is halfway between \(m\) and \(n\). Remember this statement can ALWAYS be expressed as: \(\frac{m+n}{2}=k\).

Also in GMAT we can often see another statement: The distance between \(p\) and \(m\) is the same as the distance between \(p\) and \(n\). Remember this statement can ALWAYS be expressed as: \(|p-m|=|p-n|\).


Back to original question:

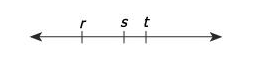Is 0 halfway between r and s?
OR is \(\frac{r+s}{2}=0\)? --> Basically the question asks is \(r+s=0\)?

(1) \(s>0\), clearly not sufficient.

(2) The distance between \(t\) and \(r\) is the same as the distance between \(t\) and -\(s\): \(|t-r|=|t+s|\).

\(t-r\) is always positive as \(r\) is to the left of the \(t\), hence \(|t-r|=t-r\);

BUT \(t+s\) can be positive (when \(t>-s\), meaning \(t\) is to the right of -\(s\)) or negative (when \(t<-s\), meaning \(t\) is to the left of -\(s\), note that even in this case \(s\) would be to the left of \(t\) and relative position of the points shown on the diagram still will be the same). So we get either \(|t+s|=t+s\) OR \(|t+s|=-t-s\).

In another words: \(t+s\) is the sum of two numbers from which one \(t\), is greater than \(s\). Their sum clearly can be positive as well as negative. Knowing that one is greater than another doesn't help to determine the sign of their sum.

Hence:
\(t-r=t+s\) --> \(-r=s\);
OR
\(t-r=-t-s\) --> \(2t=r-s\).

So the only thing we can determine from (2) is: \(t-r=|t+s|\)
Not sufficient.

(1)+(2) \(s>0\) and \(t-r=|t+s|\). \(s>0\) --> \(t>0\) (as \(t\) is to the right of \(s\)) hence \(t+s>0\). Hence \(|t+s|=t+s\). --> \(t-r=t+s\) --> \(-r=s\). Sufficient.

Answer: C.



This is not correct. If we were able to determine that \(-s=r\), statement (2) would be sufficient. But from (2) we can only say that \(t-r=|t+s|\).



As for \(s\) to be zero: from statement (1) we can say that \(s\) can not be zero as it states that \(s>0\).

For (2) we don't know whether -s=s=0 or not. If \(-s=s=0\), \(s\) and therefore -\(s\) are to the left of \(t\) and (2) would be sufficient in this case. But we don't know that.

About the relative position of the points on diagram. Do you remember the question about the two circles and point C? (https://gmatclub.com/forum/ds-area-betw ... 85958.html) I didn't know at that time if we could trust the diagram about the C being in the circle or not. You said we should, and you were right. I asked this question to Ian Stewart and he gave me the explanation about the "trust" of the diagrams in GMAT:

"In general, you should not trust the scale of GMAT diagrams, either in Problem Solving or Data Sufficiency. It used to be true that Problem Solving diagrams were drawn to scale unless mentioned otherwise, but I've seen recent questions where that is clearly not the case. So I'd only trust a diagram I'd drawn myself. ...

Here I'm referring only to the scale of diagrams; the relative lengths of line segments in a triangle, for example. ... You can accept the relative ordering of points and their relative locations as given (if the vertices of a pentagon are labeled ABCDE clockwise around the shape, then you can take it as given that AB, BC, CD, DE and EA are the edges of the pentagon; if a line is labeled with four points in A, B, C, D in sequence, you can take it as given that AC is longer than both AB and BC; if a point C is drawn inside a circle, unless the question tells you otherwise, you can assume that C is actually within the circle; if what appears to be a straight line is labeled with three points A, B, C, you can assume the line is actually straight, and that B is a point on the line -- the GMAT would never include as a trick the possibility that ABC actually form a 179 degree angle that is imperceptible to the eye, to give a few examples).

So don't trust the lengths of lines, but do trust the sequence of points on a line, or the location of points within or outside figures in a drawing. "

Hope it helps.

I have a doubt regarding such questions, since we are given a diagram, is it safe to assume that all of them have distinct values. Like is it safe to assume that here r, s, t are different

On the number line shown, is zero halfway between r and s?

(1) s is to the right of zero
(2) The distance between t and r is the same as the distance between t and -s

1)

Case I:
-----r--0--s----t---
0 is midway between r & s.

Case II:
--0--r----s----t---
0 is not midway between r & s.

Not Sufficient.

2)
Case I:
Let's say r=-s;
r=-2; s=2 t =3
-----r--0--s----t---
|t-r| = |3-(-2)|=5
|t-s| = |3-(-2)|=5
0 is midway between r and s.

Case II:
Let's say r=-s;
r=-4; s=-2 t =-1; -s=2
-----r--s--t--0----(-s)
|t-r| = |-1-(-4)|=3
|t-s| = |-1-(2)|=3
0 is not midway between r and s.
Not Sufficient.

Combining both;

r=-2; s=2 t =3
-----r--0--s----t---
|t-r| = |3-(-2)|=5
|t-s| = |3-(-2)|=5
0 is midway between r and s.

Sufficient.

Ans: "C"