If 4/x < 1/3 , what is the possible range of values of x?

Oldest

Best Reply

Author

Message

TAGS:

Intern

Status: :O

Joined: 11 Jul 2012

Posts: 43

GMAT 1: 670 Q48 V35

Followers: 0

Kudos [?]: 16 [0], given: 27

If 4/x < 1/3 , what is the possible range of values of x? [#permalink]

25 Aug 2012, 01:47

If \frac{4}{x} <\frac{1}{3} , what is the possible range of values of x?

The question is from an MGMAT guide and the solution provided multiplies the inequality by x and flips the sign to arrive at the solution x < 0 or x > 12 . However the way I naturally would solve the given equation is:
\frac{4}{x} - \frac{1}{3} < 0
\frac{(12 - x)}{(3x)} < 0

Two cases:
a) 12 - x < 0 &3x > 0 :: x > 12 & x > 0 therefore x > 12
b) 12 - x > 0 & 3x < 0 :: x < 12 & x < 0 therefore x < 12
Hence my solution: x < 12 or x > 12

Can someone kindly explain where I went wrong here?
_________________

disaster-spelled-in-670-ways-10-not-to-do-s-139230.html
GMAT Demystified: gmat-demystified-great-ebook-to-get-started-with-download-140836.html
Tense Tutorial: uber-awesome-resource-on-tenses-download-140837.html
CR Question Bank (LSAT): critical-reasoning-question-bank-download-140838.html

Manhattan GMAT Discount Codes

Kaplan GMAT Prep Discount Codes

GMAT Pill GMAT Discount Codes

GMAT Club team member

Joined: 02 Sep 2009

Posts: 11519

Followers: 1795

Kudos [?]: 9547 [1] , given: 826

Re: If 4/x < 1/3 , what is the possible range of values of x? [#permalink]

25 Aug 2012, 02:46

This post received
KUDOS

harshvinayak wrote:

When we consider the case when 12 - x > 0 and 3x < 0, we have: x<12and x<0, therefore x<0.

Solving inequalities:
inequalities-trick-91482.html (check this one first)
x2-4x-94661.html#p731476
data-suff-inequalities-109078.html
range-for-variable-x-in-a-given-inequality-109468.html?hilit=extreme#p873535
everything-is-less-than-zero-108884.html?hilit=extreme#p868863

Hope it helps.
_________________

PLEASE READ AND FOLLOW: 11 Rules for Posting!!!

RESOURCES: [GMAT MATH BOOK]; 1. Triangles; 2. Polygons; 3. Coordinate Geometry; 4. Factorials; 5. Circles; 6. Number Theory

COLLECTION OF QUESTIONS:
PS: 1. Tough and Tricky questions; 2. Hard questions; 3. Hard questions part 2; 4. Standard deviation; 5. Tough Problem Solving Questions With Solutions; 6. Probability and Combinations Questions With Solutions; 7 Tough and tricky exponents and roots questions; 8 12 Easy Pieces (or not?); 9 Bakers' Dozen; 10 Algebra set. NEW!!!

DS: 1. DS tough questions; 2. DS tough questions part 2; 3. DS tough questions part 3; 4. DS Standard deviation; 5. Inequalities; 6. 700+ GMAT Data Sufficiency Questions With Explanations; 7 Tough and tricky exponents and roots questions; 8 The Discreet Charm of the DS ; 9 Devil's Dozen!!!; 10 Number Properties set. NEW!!!

What are GMAT Club Tests?
25 extra-hard Quant Tests

Find out what's new at GMAT Club - latest features and updates

Director

Joined: 22 Mar 2011

Posts: 608

WE: Science (Education)

Followers: 43

Kudos [?]: 267 [1] , given: 43

Re: If 4/x < 1/3 , what is the possible range of values of x? [#permalink]

25 Aug 2012, 03:50

This post received
KUDOS

harshvinayak wrote:

Another way to solve this type of inequality:

From \frac{4}{x}<\frac{1}{3} it follows that x\neq0, therefore we can multiply both sides by 3x^2, which is positive.
We obtain 12x<x^2 or x^2-12x>0.
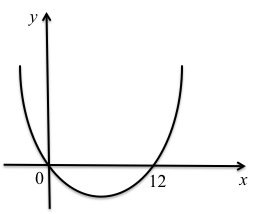
Now, imagine the graph of the quadratic function, y=12x^2-x, which is an upward parabola. See the attached drawing.
This parabola intercepts the X-axis at x=0 and x=12, the two "arms" are above the X-axis, meaning the values of y are positive when x<12 or x>0, and the values of y are negative (graph under the X-axis) when 0<x<12.

Hence the solution x<0 or x>12.

Note: Just remember the shape of the parabola, then you can easily deduce the sign of the quadratic function y=x^2+bx+c. If the quadratic equation x^2+bx+c=0 has two roots x_1<x_2 then y<0 (negative) between the two roots and y>0 (positive) outside the roots.
Or succinctly, y>0 if x_1<x<x_2 and y>0 if x<x_1 or x>x_2.

Attachments

ParabolaUp.jpg [ 8.97 KiB | Viewed 569 times ]

_________________

PhD in Applied Mathematics
Love GMAT Quant questions and running.

Intern

Status: :O

Joined: 11 Jul 2012

Posts: 43

GMAT 1: 670 Q48 V35

Followers: 0

Kudos [?]: 16 [0], given: 27

Re: If 4/x < 1/3 , what is the possible range of values of x? [#permalink]

25 Aug 2012, 04:06

Ah!

thanks for the clarification Bunuel. I guess staying up all night took its toll. I had to reread and reread and reread and...

finally what I did was (per the first link you suggested) ::

dumping the two cases,
\frac{(12-x)}{(3x)} < 0
\frac{(x-12)}{(3x)} > 0 :idea:

roots: 12 and 0
and then I could ride the waves of + - + ...... weeeeeeeeeee.... weeeeeeeeeee... and weeeeeeeeeeee :-D

Thanks again for helping out Bunuel ..

_________________

Intern

Status: :O

Joined: 11 Jul 2012

Posts: 43

GMAT 1: 670 Q48 V35

Followers: 0

Kudos [?]: 16 [0], given: 27

Re: If 4/x < 1/3 , what is the possible range of values of x? [#permalink]

25 Aug 2012, 04:15

Thanks EvaJager

you guys are awesome \m/

PS: I have just started out with my prep and have a lot to learn (and ask :lol:

) in little less than 3 weeks.
_________________

Manager

Joined: 05 Jul 2012

Posts: 83

Location: India

Concentration: Finance, Strategy

GMAT Date: 09-30-2012

GPA: 3.08

WE: Engineering (Energy and Utilities)

Followers: 4

Kudos [?]: 6 [0], given: 8

Re: If 4/x < 1/3 , what is the possible range of values of x? [#permalink]

26 Aug 2012, 11:24

harshvinayak wrote:

Thanks EvaJager

you guys are awesome \m/

PS: I have just started out with my prep and have a lot to learn (and ask :lol:

) in little less than 3 weeks.

One way to understand this is that Sign of \frac{x-a}{x-b} is same as the sign of (x-a)(x-b)
and for (x-a)(x-b) always remember that it will be negative between a & b and positive outside a & b

Veritas Prep GMAT Instructor

Joined: 16 Oct 2010

Posts: 3107

Location: Pune, India

Followers: 568

Kudos [?]: 2000 [1] , given: 92

Re: If 4/x < 1/3 , what is the possible range of values of x? [#permalink]

28 Aug 2012, 21:58

This post received
KUDOS

harshvinayak wrote:

Check out these posts. They discuss how to solve inequalities efficiently (using the wave) and how to handle various complications that can arise in a question.

http://www.veritasprep.com/blog/2012/06 ... e-factors/
http://www.veritasprep.com/blog/2012/07 ... ns-part-i/
http://www.veritasprep.com/blog/2012/07 ... s-part-ii/
http://www.veritasprep.com/blog/2012/07 ... qualities/
_________________

Karishma
Veritas Prep | GMAT Instructor
My Blog

Save 10% on Veritas Prep GMAT Courses And Admissions Consulting
Enroll now. Pay later. Take advantage of Veritas Prep's flexible payment plan options.

Veritas Prep Reviews

Intern

Status: :O

Joined: 11 Jul 2012

Posts: 43

GMAT 1: 670 Q48 V35

Followers: 0

Kudos [?]: 16 [0], given: 27

Re: If 4/x < 1/3 , what is the possible range of values of x? [#permalink]

28 Aug 2012, 22:16

WOW !

Thanks Karishma, thats one awesome collection of inequalities stuff. A kudos alone wouldnt have cut it :-D

_________________

Re: If 4/x < 1/3 , what is the possible range of values of x? [#permalink] 28 Aug 2012, 22:16

		Similar topics	Author	Replies	Last post
Similar Topics:		if x<0 what is the value of ^1/4+(-x*\|x\|)^1/2	joemama142000	8	14 Apr 2006, 17:24
		if x<0, what is the value of ^1/4+(-x*\|x\|)^1/2 i guess	MA	5	18 Jul 2006, 14:40
	3	For what range of values of 'x' ?	Eden	7	03 Sep 2010, 07:02
		4^x + 4 ^-x = 2 What is the value of X	nimc2012	4	07 Feb 2012, 09:56
		What is the value of (4x-y)*1/(3y)?	macjas	1	27 May 2012, 09:13

If 4/x < 1/3 , what is the possible range of values of x?

Main navigation

GMAT Resources

Partners

MBA Resources

GMAT ® is a registered trademark of the Graduate Management Admission Council ® (GMAC ®). GMAT Club's website has not been reviewed or endorsed by GMAC.