Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
gurpreetsingh
Joined: 12 Oct 2009
Last visit: 15 Jun 2019
Posts: 2,272
Given Kudos: 235
Status:<strong>Nothing comes easy: neither do I want.</strong>
Location: Malaysia
Concentration: Technology, Entrepreneurship
Schools: ISB '15 (M)
GMAT 1: 670 Q49 V31

GMAT 2: 710 Q50 V35

Originally posted by gurpreetsingh on 16 Mar 2010, 10:11.
Last edited by Bunuel on 26 Apr 2018, 03:34, edited 1 time in total.
Last edited by Bunuel on 26 Apr 2018, 03:34, edited 1 time in total.
Edited.
Kudos
Bookmarks
I learnt this trick while I was in school and yesterday while solving one question I recalled.
Its good if you guys use it 1-2 times to get used to it.
Suppose you have the inequality
\(f(x) = (x-a)(x-b)(x-c)(x-d) < 0\)
Just arrange them in order as shown in the picture and draw curve starting from + from right.
now if f(x) < 0 consider curve having "-" inside and if f(x) > 0 consider curve having "+" and combined solution will be the final solution. I m sure I have recalled it fully but if you guys find any issue on that do let me know, this is very helpful.
Don't forget to arrange then in ascending order from left to right. \(a<b<c<d\)
So for f(x) < 0 consider "-" curves and the ans is: \((a < x < b)\), \((c < x < d)\)
and for f(x) > 0 consider "+" curves and the ans is: \((x < a)\), \((b < x < c)\), \((d < x)\)
If f(x) has three factors then the graph will have - + - +
If f(x) has four factors then the graph will have + - + - +
If you can not figure out how and why, just remember it.
Try to analyze that the function will have number of roots = number of factors and every time the graph will touch the x axis.
For the highest factor d if x>d then the whole f(x) > 0 and after every interval of the roots the signs will change alternatively.
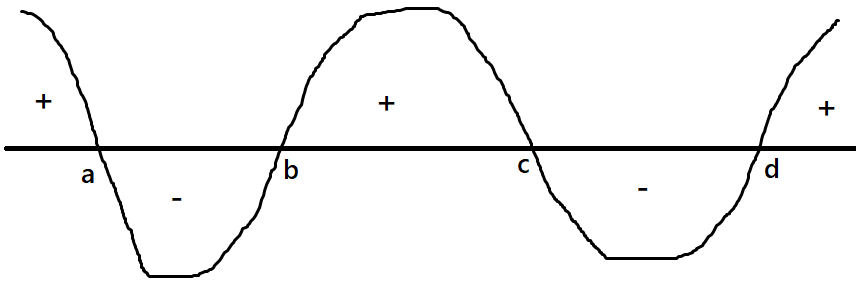

1.jpg [ 6.73 KiB | Viewed 121869 times ]

Untitled.png [ 12.08 KiB | Viewed 67327 times ]
Its good if you guys use it 1-2 times to get used to it.
Suppose you have the inequality
\(f(x) = (x-a)(x-b)(x-c)(x-d) < 0\)
Just arrange them in order as shown in the picture and draw curve starting from + from right.
now if f(x) < 0 consider curve having "-" inside and if f(x) > 0 consider curve having "+" and combined solution will be the final solution. I m sure I have recalled it fully but if you guys find any issue on that do let me know, this is very helpful.
Don't forget to arrange then in ascending order from left to right. \(a<b<c<d\)
So for f(x) < 0 consider "-" curves and the ans is: \((a < x < b)\), \((c < x < d)\)
and for f(x) > 0 consider "+" curves and the ans is: \((x < a)\), \((b < x < c)\), \((d < x)\)
If f(x) has three factors then the graph will have - + - +
If f(x) has four factors then the graph will have + - + - +
If you can not figure out how and why, just remember it.
Try to analyze that the function will have number of roots = number of factors and every time the graph will touch the x axis.
For the highest factor d if x>d then the whole f(x) > 0 and after every interval of the roots the signs will change alternatively.
Attachment:
1.jpg [ 6.73 KiB | Viewed 121869 times ]
Attachment:
Untitled.png [ 12.08 KiB | Viewed 67327 times ]
Yes, this is a neat little way to work with inequalities where factors are multiplied or divided. And, it has a solid reasoning behind it which I will just explain.
If (x-a)(x-b)(x-c)(x-d) < 0, we can draw the points a, b, c and d on the number line.
e.g. Given (x+2)(x-1)(x-7)(x-4) < 0, draw the points -2, 1, 7 and 4 on the number line as shown.
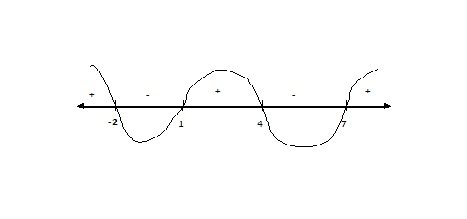
doc.jpg [ 7.9 KiB | Viewed 124595 times ]
This divides the number line into 5 regions. Values of x in right most region will always give you positive value of the expression. The reason for this is that if x > 7, all factors above will be positive.
When you jump to the next region between x = 4 and x = 7, value of x here give you negative value for the entire expression because now, (x - 7) will be negative since x < 7 in this region. All other factors are still positive.
When you jump to the next region on the left between x = 1 and x = 4, expression will be positive again because now two factors (x - 7) and (x - 4) are negative, but negative x negative is positive... and so on till you reach the leftmost section.
Since we are looking for values of x where the expression is < 0, here the solution will be -2 < x < 1 or 4< x < 7
It should be obvious that it will also work in cases where factors are divided.
e.g. (x - a)(x - b)/(x - c)(x - d) < 0
(x + 2)(x - 1)/(x -4)(x - 7) < 0 will have exactly the same solution as above.
Note: If, rather than < or > sign, you have <= or >=, in division, the solution will differ slightly. I will leave it for you to figure out why and how. Feel free to get back to me if you want to confirm your conclusion.
Here is the video explanation of this: https://youtu.be/PWsUOe77__E
If (x-a)(x-b)(x-c)(x-d) < 0, we can draw the points a, b, c and d on the number line.
e.g. Given (x+2)(x-1)(x-7)(x-4) < 0, draw the points -2, 1, 7 and 4 on the number line as shown.
Attachment:
doc.jpg [ 7.9 KiB | Viewed 124595 times ]
This divides the number line into 5 regions. Values of x in right most region will always give you positive value of the expression. The reason for this is that if x > 7, all factors above will be positive.
When you jump to the next region between x = 4 and x = 7, value of x here give you negative value for the entire expression because now, (x - 7) will be negative since x < 7 in this region. All other factors are still positive.
When you jump to the next region on the left between x = 1 and x = 4, expression will be positive again because now two factors (x - 7) and (x - 4) are negative, but negative x negative is positive... and so on till you reach the leftmost section.
Since we are looking for values of x where the expression is < 0, here the solution will be -2 < x < 1 or 4< x < 7
It should be obvious that it will also work in cases where factors are divided.
e.g. (x - a)(x - b)/(x - c)(x - d) < 0
(x + 2)(x - 1)/(x -4)(x - 7) < 0 will have exactly the same solution as above.
Note: If, rather than < or > sign, you have <= or >=, in division, the solution will differ slightly. I will leave it for you to figure out why and how. Feel free to get back to me if you want to confirm your conclusion.
Here is the video explanation of this: https://youtu.be/PWsUOe77__E
Kudos
Bookmarks
WoW - This is a cool thread with so many thing on inequalities....I have compiled it together with some of my own ideas...It should help.
1) CORE CONCEPT
@gurpreetsingh -
Suppose you have the inequality
f(x) = (x-a)(x-b)(x-c)(x-d) < 0
Arrange the NUMBERS in ascending order from left to right. a<b<c<d
Draw curve starting from + from right.
now if f(x) < 0 consider curve having "-" inside and if f(x) > 0 consider curve having "+" and combined solution will be the final solution. I m sure I have recalled it fully but if you guys find any issue on that do let me know, this is very helpful.
So for f(x) < 0 consider "-" curves and the ans is : (a < x < b) , (c < x < d)
and for f(x) > 0 consider "+" curves and the ans is : (x < a), (b < x < c) , (d < x)
If f(x) has three factors then the graph will have - + - +
If f(x) has four factors then the graph will have + - + - +
If you can not figure out how and why, just remember it.
Try to analyze that the function will have number of roots = number of factors and every time the graph will touch the x axis.
For the highest factor d if x>d then the whole f(x) > 0 and after every interval of the roots the signs will change alternatively.
Note: Make sure that the factors are of the form (ax - b), not (b - ax)...
example -
(x+2)(x-1)(7 - x)<0
Convert this to: (x+2)(x-1)(x-7)>0 (Multiply both sides by '-1')
Now solve in the usual way. Assign '+' to the rightmost region and then alternate with '-'
Since you are looking for positive value of the expression, every region where you put a '+' will be the region where the expression will be greater than 0.
2) Variation - ODD/EVEN POWER
@ulm/Karishma -
if we have even powers like (x-a)^2(x-b)
we don't need to change a sign when jump over "a".
This will be same as (x-b)
We can ignore squares BUT SHOULD consider ODD powers
example -
2.a
(x-a)^3(x-b)<0 is the same as (x-a)(x-b) <0
2.b
(x - a)(x - b)/(x - c)(x - d) < 0 ==> (x - a)(x - b)(x-c)^-1(x-d)^-1 <0
is the same as (x - a)(x - b)(x - c)(x - d) < 0
3) Variation <= in FRACTION
@mrinal2100 -
if = sign is included with < then <= will be there in solution
like for (x+2)(x-1)(x-7)(x-4) <=0 the solution will be -2 <= x <= 1 or 4<= x <= 7
BUT if it is a fraction the denominator in the solution will not have = SIGN
example -
3.a
(x + 2)(x - 1)/(x -4)(x - 7) < =0
the solution will be -2 <= x <= 1 or 4< x < 7
we cant make 4<=x<=7 as it will make the solution infinite
4) Variation - ROOTS
@Karishma -
As for roots, you have to keep in mind that given \(\sqrt{x}\), x cannot be negative.
\(\sqrt{x}\) < 10
implies 0 < \(\sqrt{x}\) < 10
Squaring, 0 < x < 100
Root questions are specific. You have to be careful. If you have a particular question in mind, send it.
Refer - inequalities-and-roots-118619.html#p959939
Some more useful tips for ROOTS....I am too lazy to consolidate
<5> THESIS -
@gmat1220 -
Once algebra teacher told me - signs alternate between the roots. I said whatever and now I know why Watching this article is a stroll down the memory lane.
Watching this article is a stroll down the memory lane.
I will save this future references....
Please add anything that you feel will help.
Anyone wants to add ABSOLUTE VALUES....That will be a value add to this post
1) CORE CONCEPT
@gurpreetsingh -
Suppose you have the inequality
f(x) = (x-a)(x-b)(x-c)(x-d) < 0
Arrange the NUMBERS in ascending order from left to right. a<b<c<d
Draw curve starting from + from right.
now if f(x) < 0 consider curve having "-" inside and if f(x) > 0 consider curve having "+" and combined solution will be the final solution. I m sure I have recalled it fully but if you guys find any issue on that do let me know, this is very helpful.
So for f(x) < 0 consider "-" curves and the ans is : (a < x < b) , (c < x < d)
and for f(x) > 0 consider "+" curves and the ans is : (x < a), (b < x < c) , (d < x)
If f(x) has three factors then the graph will have - + - +
If f(x) has four factors then the graph will have + - + - +
If you can not figure out how and why, just remember it.
Try to analyze that the function will have number of roots = number of factors and every time the graph will touch the x axis.
For the highest factor d if x>d then the whole f(x) > 0 and after every interval of the roots the signs will change alternatively.
Note: Make sure that the factors are of the form (ax - b), not (b - ax)...
example -
(x+2)(x-1)(7 - x)<0
Convert this to: (x+2)(x-1)(x-7)>0 (Multiply both sides by '-1')
Now solve in the usual way. Assign '+' to the rightmost region and then alternate with '-'
Since you are looking for positive value of the expression, every region where you put a '+' will be the region where the expression will be greater than 0.
2) Variation - ODD/EVEN POWER
@ulm/Karishma -
if we have even powers like (x-a)^2(x-b)
we don't need to change a sign when jump over "a".
This will be same as (x-b)
We can ignore squares BUT SHOULD consider ODD powers
example -
2.a
(x-a)^3(x-b)<0 is the same as (x-a)(x-b) <0
2.b
(x - a)(x - b)/(x - c)(x - d) < 0 ==> (x - a)(x - b)(x-c)^-1(x-d)^-1 <0
is the same as (x - a)(x - b)(x - c)(x - d) < 0
3) Variation <= in FRACTION
@mrinal2100 -
if = sign is included with < then <= will be there in solution
like for (x+2)(x-1)(x-7)(x-4) <=0 the solution will be -2 <= x <= 1 or 4<= x <= 7
BUT if it is a fraction the denominator in the solution will not have = SIGN
example -
3.a
(x + 2)(x - 1)/(x -4)(x - 7) < =0
the solution will be -2 <= x <= 1 or 4< x < 7
we cant make 4<=x<=7 as it will make the solution infinite
4) Variation - ROOTS
@Karishma -
As for roots, you have to keep in mind that given \(\sqrt{x}\), x cannot be negative.
\(\sqrt{x}\) < 10
implies 0 < \(\sqrt{x}\) < 10
Squaring, 0 < x < 100
Root questions are specific. You have to be careful. If you have a particular question in mind, send it.
Refer - inequalities-and-roots-118619.html#p959939
Some more useful tips for ROOTS....I am too lazy to consolidate
<5> THESIS -
@gmat1220 -
Once algebra teacher told me - signs alternate between the roots. I said whatever and now I know why
I will save this future references....
Please add anything that you feel will help.
Anyone wants to add ABSOLUTE VALUES....That will be a value add to this post







