Graphic approach to problems with inequalities

Can we use this technique to solve any of the in equality ques. My accuracy in such questions suffer.
Please mention how I should approach in equalities.....

Can you please tell me how do you know which region to shade?
I mean , to the left? or right? above or below the x axis?

How do you find out

I don't understand how we can deduce from (2) that its not sufficient. What I see from the graph, is that y-x=2 never pass the red area. How am I supposed to interpret that graph?

All the other graphs makes sense "Oh okay, don't have any line passing the red part = sufficient" - but the last figure doesn't go through red zone either, yet still insufficient?

Am I supposed to realize that the lines can't pass through that white area just above "TRUE" either?

When the thread gets to the 6th page with, presumably, multiple solutions, you need to quote the post to which you are referring or give its link.

Figure 5. Original post. The line y-x=2 never goes through the red zone - yet "insufficient"

Bunuel / Chetan2u / Karishma : Your solution to this problem please ?


Thanks
Regards

If \(\frac{x}{y} > 2\), is \(3x + 2y < 18\)?


\(\frac{x}{y}>2\) tells us that \(x\) and \(y\) are either both positive or both negative, which means that all points \((x,y)\) satisfying given inequality are either in I or III quadrant. When they are both negative (in III quadrant) inequality \(3x+2y<18\) is always true, so we should check only for I quadrant, or when both \(x\) and \(y\) are positive.

In I quadrant, as \(x\) and \(y\) are both positive, we can rewrite \(\frac{x}{y}>2\) as \(x>2y>0\) (remember \(x>0\) and \(y>0\)).

So basically question becomes: If \(x>0\) and \(y>0\) and \(x>2y>0\), is \(3x+2y<18\)?


(1) \(x-y<2\).

Subtract inequalities \(x>2y\) and \(x-y<2\) (we can do this as signs are in opposite direction) --> \(x-(x-y)>2y-2\) --> \(y<2\).

Now add inequalities \(x-y<2\) and \(y<2\) (we can do this as signs are in the same direction) --> \(x-y+y<2+2\) --> \(x<4\).

We got \(y<2\) and \(x<4\). If we take maximum values \(x=4\) and \(y=2\) and substitute in \(3x+2y<18\), we'll get \(12+4=16<18\).

Sufficient.


(2) \(y-x<2\) and \(x>2y\):
\(x=3\) and \(y=1\) --> \(3x+2y=11<18\) true.
\(x=11\) and \(y=5\) --> \(3x+2y=43<18\) false.

Not sufficient.


Answer: A.

THIS QUESTION IS DISCUSSED HERE.

Bunuel I have one doubt. if we see the algebraic approach, the the first condition gives us the solution as y<2 and x<4. However, if i see the graphical approach, these values doesn't satisfy the graphical area satisfied by original condition and condition-1. Clarify where am I going wrong?

Check the graph below:


Blue region satisfies the following conditions:
\(x>0\) and \(y>0\) and \(x>2y>0\)
\(x-y<2\).

As you can see for that region \(y<2\) and \(x<4\) holds true.

Check the graph below:


Blue region satisfies the following conditions:
\(x>0\) and \(y>0\) and \(x>2y>0\)
\(x-y<2\).

As you can see for that region \(y<2\) and \(x<4\) holds true.

Bunuel
Bunuel, what if we select values x=3.9 and y=0.1.
It satisfies x>0 y>0 x<4 and y<2. However, I observe that this point doesn't come in graphical solution.please explain.

Posted from my mobile device

Bunuel I have one doubt. if we see the algebraic approach, the the first condition gives us the solution as y<2 and x<4. However, if i see the graphical approach, these values doesn't satisfy the graphical area satisfied by original condition and condition-1. Clarify where am I going wrong?

Bunuel
I see. So, as per our discussion, I conclude that algebraically method of solving has a limitation in the way that it provides superset of solution unlike graphical approach, which gives precisely the solution set only. Am I correct?
However, it seems weird to me since I used to see inequality algebraic method in the other way. For example, if x>5 and y<2 that implies x-y>3; the solution is so precise that every point greater than 3 satisfies the equation. So, still not very clear.

Hi all! My friend Tarek PMed me and asked to show how to use the graphic approach to problems with inequalities. I really love the approach because it isn't only fast one after training, but also reliable. So, I try to illustrate how to use it.

:fyi There are two distinct ways to solve math problems: logical and visual. The approach described in this post is for those who use the visual approach. If you like imaging math problems in the visual scratchpad in your mind, you will enjoy this method. At the same time, don't be discourage if it doesn't work for you, try the logical approach instead (described by Bunuel).

If \(\frac{x}{y}>2\), is \(3x+2y<18?\)

(1) \(x-y\) is less than \(2\)
(2) \(y-x\) is less than \(2\)

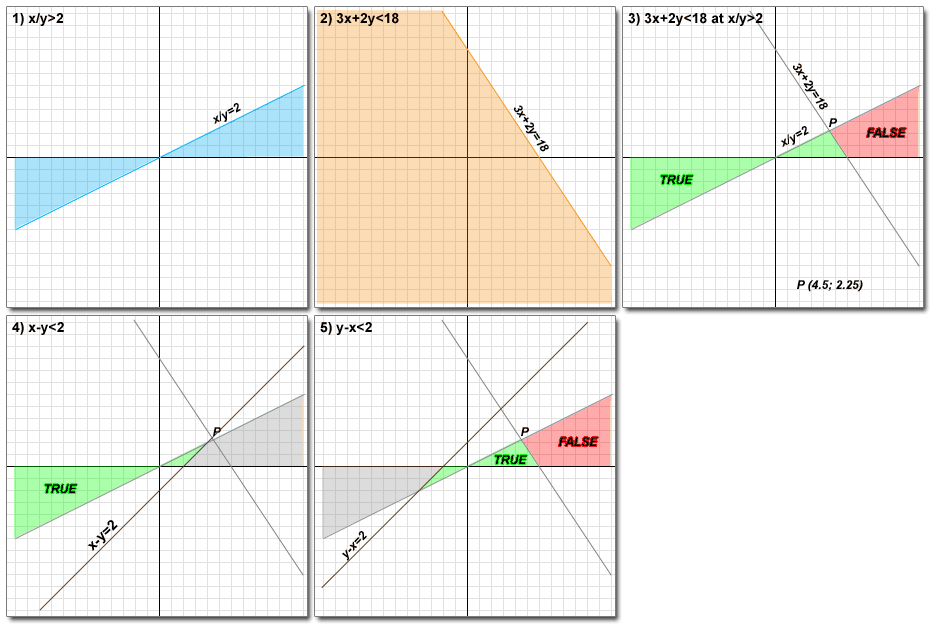
1. First of all, we draw x/y>2. x/y=2 - is a boundary. (see figure 1). we should note that if one of the variables is negative and other is positive, x/y will be always negative and less than 2. Therefore, our set of x,y that satisfied x/y>2 lies between line x/y=2 and x-axis.

2. Next, we draw our main inequality: 3x+2y<18. 3x+2y=18 - is a boundary. (see figure 2).

3. Now, we should combine our main inequality with the restriction, x/y>2. (see figure 3). Eventually, we defined two areas (sets) were the main inequality is TRUE and were it is FALSE. Two lines intersect in point P with coordinates: (4.5;2.25).

4. Let's consider fist condition: x-y<2. x-y=2 is a boundary. (see figure 4). As we can see all y,x that satisfies the fist condition lie in "green-TRUE" region. Therefore, the first statement is sufficient to answer the question. We should be careful and check where line x-y=2 passes point P, through left side or right side. We can put y=2.25 into x-y=2 and find that x=4.25<4.5 (left side). In other words, line x-y=2 passes y=2.25 (y-coordinate of P) early and goes above P.

5. Finally, let's check last condition: y-x<2. y-x=2 is a boundary. (see figure 5). As we can see all y,x that satisfies the second condition lie in both "green-TRUE" and "red-FALSE" regions. Thus, the second condition is insufficient.

So, answer is A.

This approach took less than 2 minutes.



Tips:

1) How fast can we draw a line, for example 3x+2y=18? Simple approach: we need two points to draw line, let's choose intersections with x- and y- axes. x=0 (intersection with y-axis) --> y=9; y=0 (intersection with x-axis) --> x=6.

2) Let's suppose we have a linear inequality, such as 38y-11x>121, suppose we've already drawn the line. How can we find what side is "true" and what side is "false"? The fastest method is just use y=0,x=-infinity. In our case, 0-(-infinity)=infinity>121 - true. Therefore, we take a left side.

See also: THIS QUESTION

That's all
Regards,
Walker