Bunuel wrote:
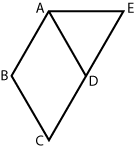 Quadrilateral ABCD is a rhombus and points C, D, and E are on the same line. Is quadrilateral ABDE a rhombus?
Quadrilateral ABCD is a rhombus and points C, D, and E are on the same line. Is quadrilateral ABDE a rhombus?Rhombus is a quadrilateral with all four sides equal in length. A rhombus is actually just a special type of parallelogram (just like square or rectangle).
So ABCD is a rhombus means AB=BC=CD=AD.
ABDE to be a rhombus it must be true that AB=BD=DE=AE.
(1) The measure of angle BCD is 60 degrees --> diagonal BD equals to the sides of rhombus, so BD=AB. Know nothing about DE or/and AE. Not sufficient.
(2) AE is parallel to BD --> ABDE is a parallelogram (as AE||BD and BA||DE), hence opposite sides are equal: BD=AE and AB=DE. But we don't know whether all sides are equal (AB=BD=DE=AE). Not sufficient.
(1)+(2) From (1): BD=AB and from (2) BD=AE and AB=DE --> AB=BD=DE=AE --> ABDE is a rhombus. Sufficient.
Answer: C.
Hi Bunuel,
I'm trying to catch my disconnect and tried to explain the reasoning. Appreciate any input.
1. From the question stem, we know that AB=BC=CD=DA because it's a rhombus. We cannot infer the exact degree's besides stating that the opposite angles will be equal and the adjacent will add up to 180.
Is that correct to infer?2, Additionally, we are told/asked "Is quadrilateral ABDE a rhombus?" -- It does say that ABDE is a
quadrilateral, meaning, that the lines AE and BD should be parallel and AB and DE should be parallel.
Is that correct to infer? I'm guessing the answer is NO. Maybe i'm confusing quadrilateral with parallelogram?Now, according to statement A = If I know that BCD is 60 degrees, I can automatically infer that BAD is 60 degrees since it's a rhombus. This makes ADE 60 degrees but I don't know anything about the other two angles DAE and DEA.
INSUFFICIENT
3. Additionally, statement two states that (2) AE is parallel to BD. Now I can infer that since AE is parallel to BD and since BA is parallel to DE, it's at least a parallelogram.
Correct?
Now, since I know that it's a parallelogram, I can work my way through the angles and realize that it's a parallelogram with all acute angles equal to each other and all obtuse equal to each other. I also know that BC = BD = BA, therefore a Rhombus.
1 is correct.
2 is not correct. Quadrilateral just means "four sides". So, any four-sided shape is a quadrilateral.




















