Hello!
Just some basics facts about inequalities.Feel free to add-on/correct mistakes.
I. Given that x>y\(x^n>y^n\) is always true for n = odd Example \(0.5>-2 \to (0.5)^3 > (-2)^3 \to 0.125>-8\) [Correct]
\(x^n>y^n\) may or may not be true for n = even.Example \(0.5>-2 \to (0.5)^2 > (-2)^2 \to 0.25>4\) [Incorrect]
In the same vein,
Given that \(x^n>y^n\)x>y is always true for n = odd
Example \(-8>-27 \to (-2)^3 > (-3)^3 \to -2>-3\) [Correct]
x>y may or may not be true for n = evenExample \(16>1 \to (-4)^2 > 1^2 \to -4>1\)[Incorrect]
This is so because an odd power will never distort the negative character of the given quantities.
II. Given that x/y>1 [I have used 1 on the RHS for convenience, it can be any constant]
This implies \(\to\)
x>y for y>0Example \(\frac{4}{3}>1 \to 4>3\) [Correct]
x<y for y<0Example \(\frac{(-4)}{(-3)}>1 \to -4<-3\) [Correct]
This result may be extrapolated to state that any quantity, whose sign(positive or negative) is unknown in a given inequality can be safely cross-multiplied/divided for only even powers , for example\(y^2\), \(y^4\) and so on, but never for odd powers such as \(y\) , \(y^3\). If the quantity is POSITIVE, it can be safely multiplied/divided with no changes to the angle brackets(> or <) and if the quantity is negative, then the angle brackets have to be made opposite to its initial direction.
III. Given that x>y & p>qTwo inequalities may be added when the inequality's angle brackets (< or >) are in the same direction.
Thus, \(x+p>y+q\) is Correct.Two inequalities can be subtracted only when the angle brackets are in different direction.
Thus, x>y and q<p \(\to x-q>y-p\) OR \(q-x<p-y\). Notice that the direction of the angle bracket corresponding to the quantity from which the subtraction occurs,dominates.
IV. Inequalities for quadratic equations: Attachment:
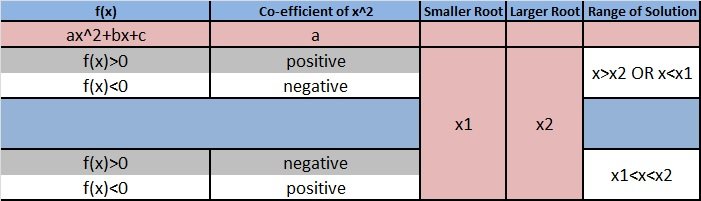 image.jpg [ 37.96 KiB | Viewed 10799 times ]
image.jpg [ 37.96 KiB | Viewed 10799 times ]
V. When a given inequality is expressed like (x-a)(x-b)(x-c)..(x-z)>0 or (x-a)(x-b)(x-c)..(x-z)<0 [/size]
Consider the f(x) = (x-a)(x-b)(x-c)...(x-z). The roots of this function are x = a, OR x = b and so on. The key to solve such inequalities is to know that the sign of any function changes between any two given roots. For example, for f(x) = (x-1)(x-2), three scenarios are possible:
Attachment:
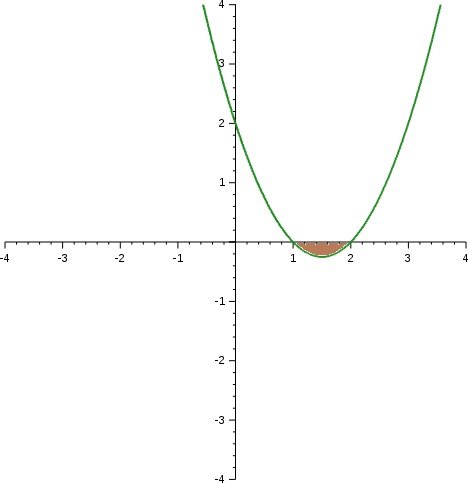 Image.jpg [ 17.84 KiB | Viewed 11127 times ]
Image.jpg [ 17.84 KiB | Viewed 11127 times ]
For x = 1 OR x = 2 --> The function f(x) is equal to zero
For any value of x in-between the roots(the shaded area), the value of f(x) will always be negative, i.e. f(x)<0.
For any value of x<1 or x>2, the value of f(x) will always be positive , i.e. f(x) >0.
Armed with this concept, it is now very easy to solve for the expressions like the one given above, All we have to do is to plot the roots on the number line(inherently in the increasing order), and assign positive sign to the right of the biggest root on the number line.
For example, for the expression f(x) = (x-1)(x+2)(x-3) , if we are supposed to find the range for f(x)>0,
Attachment:
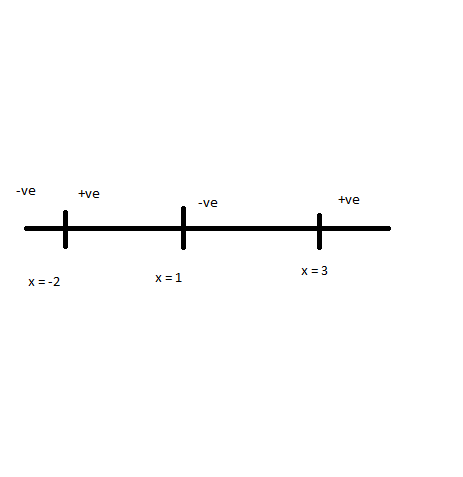 Image_2.png [ 3.36 KiB | Viewed 11104 times ]
Image_2.png [ 3.36 KiB | Viewed 11104 times ]
1. Find out the roots for f(x) --> -2 OR 1 OR 3
2. Plot on the number line --> Any value of x, to the right of x=3 on the number line will make f(x)>0. Alernatively, mark the regions between each of the root as positive/negative. Thus, for the given example, it would read as :
f(x)>0 ; x>3
f(x)<0 ; 1<x<3
f(x)>0 ; -2<x<1
f(x)<0 ; x<-2
Example 2: Find the range of x where \(\frac{(x-1)(x-2)}{(x+3)} < 0\)
For the above example, if your first thought was to cross multiply (x+3) and solve, you are not treading on the right path.We don't know anything about the sign of (x+3). However, we know one thing, and that is x \(\neq{-3}\). Thus, to get rid of the expression in the denominator, multiply on both sides of the inquality by \((x+3)^2\). Thus, we end up getting (x-1)(x-2)(x+3) < 0. Continue solving just as above.
Example 3: Find the range of x where \(\frac{(x-1)(x-2)}{(x^2+3)} >0\)
Here, we can safely cross-multiply the denominator as because for any real value of x, the term \((x^2+3)\) will always be positive.
Thus, the final expression will be (x-1)(x-2)>0. We can solve it just like above.
Hope this helps;let me know if I missed out on something.

