This question can easily be solved using the alligation diagram.
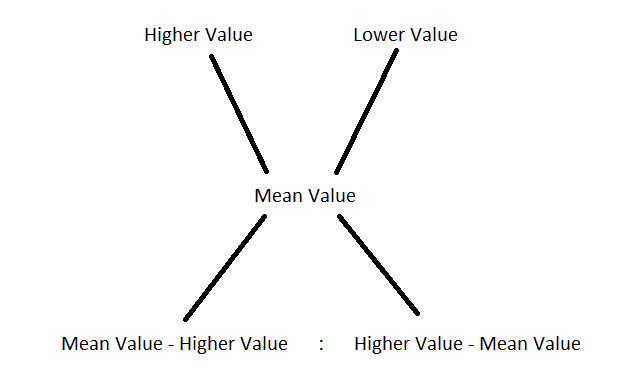
Before I jump in to solve this question, let me provide you a brief explanation of how to approach weighted average questions on the GMAT. Weighted average questions can be easily solved by making use of the alligation/mixture diagram given below.
Attachment:
 Mixtures 1.png [ 6.07 KiB | Viewed 17184 times ]
Mixtures 1.png [ 6.07 KiB | Viewed 17184 times ]
Putting in values in the alligation/mixture diagram and subtracting along the diagonals gives us a ratio in which two quantities are mixed. This ratio can now be used to find out what specific amounts of two quantities need to be mixed to obtain a particular mixture.
The only thing that you need to keep in mind here is that the values you need to use, that is the higher value, lower value and mean value have to be values which are associated with the word 'per' (percents, average, per km, per kg etc.).
The alligation/mixture diagram proves useful not only when mixing solutions or combining solids but also to explain the weighted average concept (the word average is also associated with the word per i.e. if the average marks of the class is 80, then it can be understood as 80 marks per student). Say if we have a class A where the average marks is 80 and another class B where the average marks is 70 and the combined average of both class A and B is 74, then we can definitely comment upon which class has the greater number of students. If we represent the average values in the mixture diagram, the ratio of students of Class A and Class B will be 2 : 3. This clearly indicates that class B has the greater number of students.
Now the question here tells us that the overall average (mean value) of the group is 80 and we are asked to answer if the average score of the women is greater than 85.
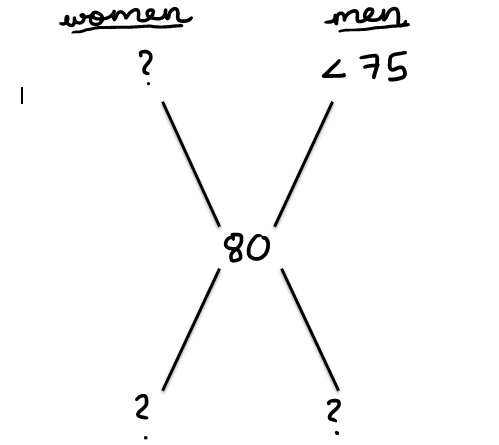
Statement 1 : The average score for the men was less than 75Attachment:
 Mixtures 2.PNG [ 17.56 KiB | Viewed 17164 times ]
Mixtures 2.PNG [ 17.56 KiB | Viewed 17164 times ]
Here we do not have any information about the ratio of men to women. So we ca consider any value for the average score of women. Insufficient.
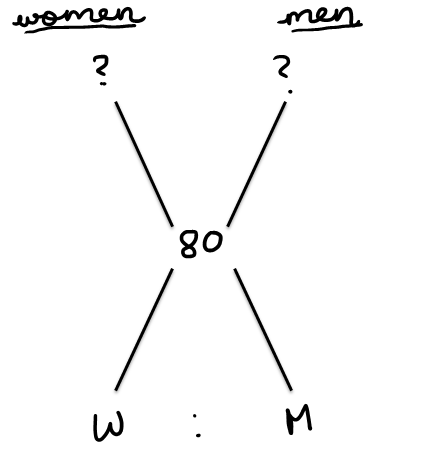
Statement 2 : The group consisted of more men than womenAttachment:
 Capture 3.PNG [ 14.98 KiB | Viewed 17141 times ]
Capture 3.PNG [ 14.98 KiB | Viewed 17141 times ]
So if the ration of W : M is 1 : 2, then the average score of the women will be 82 and the average score of the men will be 81 which gives us a NO.
If the ratio of W : M is 1 : 7, then the average score of the women will be 87 and the average score of the men will be 81 which gives us a YES.
Insufficient.
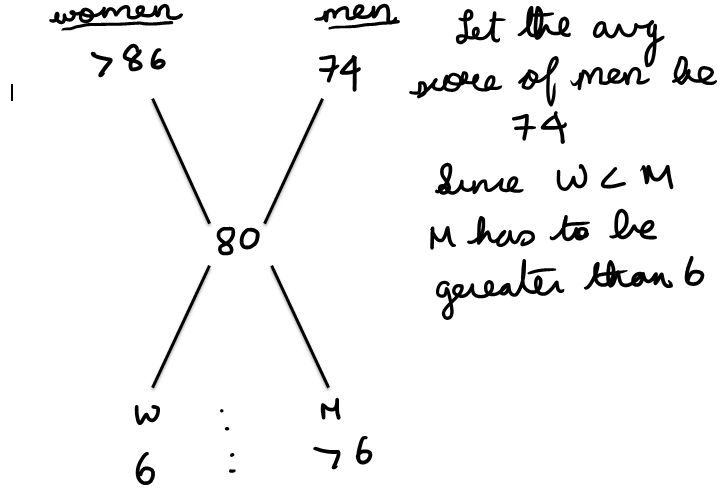
Combining 1 and 2 : We know that the average score for the men was less than 75 and the number of men is greater than the number of women.Attachment:
 Combined.PNG [ 34.91 KiB | Viewed 17146 times ]
Combined.PNG [ 34.91 KiB | Viewed 17146 times ]
So the average score for the women will always be greater than 85.
Sufficient. 


 45%
(medium)
45%
(medium)
 32%
(01:47)
wrong
32%
(01:47)
wrong  based on 3973
sessions
based on 3973
sessions










