yezz wrote:
In triangle ABC, point X is the midpoint of side AC and point Y is the midpoint of side BC. If point R is the midpoint of line segment XC and if point S is the midpoint of line segment YC, what is the area of triangular region RCS ?
(1) The area of triangular region ABX is 32.
(2) The length of one of the altitudes of triangle ABC is 8.
If we observe closesly, in this problem one vertex of the triangle is joined to the midpoint of the other side and this process is done multiple times.
Now, what is so special about the line segment joining the vertex to the midpoint of the other side? more specifically, how will it affect the area of the original triangle? Let's take a look at it.
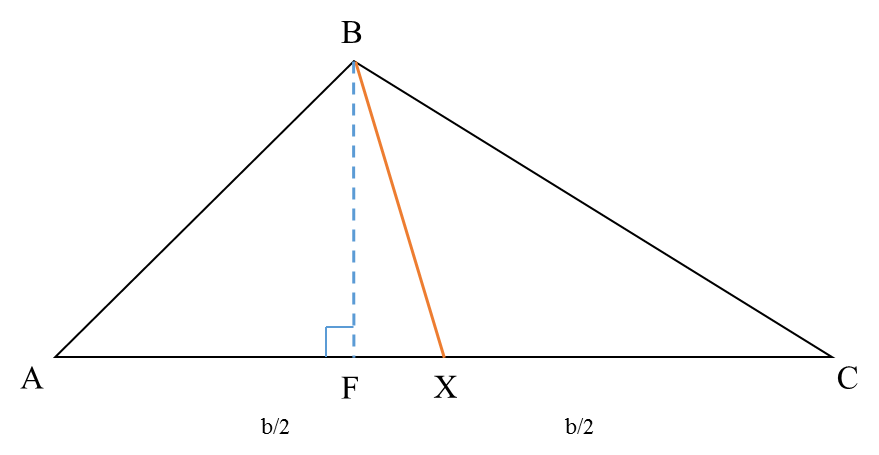
Consider a triangle ABC of area
p square units. Suppose X is the midpoint of side AC. Join B and X as shown below:
Attachment:
 median.png [ 9.81 KiB | Viewed 79259 times ]
median.png [ 9.81 KiB | Viewed 79259 times ]
What is the area of triangle ABX? Think about it...
The base became half the original size and the height of the vertex from the base remained the same.
Therefore area of the triangle ABX (\(\frac{1}{2} * base* height\)) will be half the area of the original triangle ABC i.e., \(\frac{p}{2}\) square units.
Now what is the area of triangle BXC?
\(p - \frac{p}{2} = \frac{p}{2}\) square units.
So, what did we observe?A line joining a vertex of a triangle to the midpoint of the opposite side will divide the triangle into two equal parts.
Let us call such a line as a "
sword line" of a triangle for easy reference.
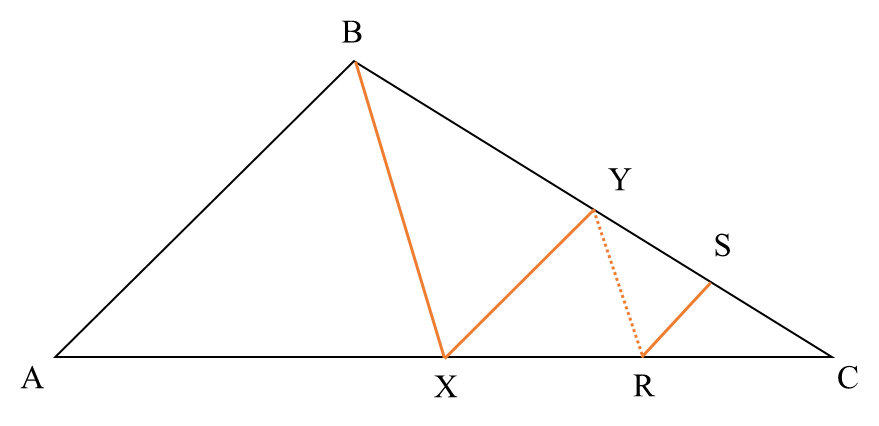
Now, with this understanding, let us look at the triangle in the given problem.
Attachment:
 OG113DS.png [ 11 KiB | Viewed 79229 times ]
OG113DS.png [ 11 KiB | Viewed 79229 times ]
If we assume that the area of triangle ABC is \(y\) square units, from our understanding we know that area of triangle BXC is \(\frac{y}{2}\) square units.
Notice that since Y is the midpoint of BC, XY is a "
sword line" in the triangle BXC.
Therefore area of triangle XYC = half of area of triangle BXC = \(\frac{y}{4}\) square units.
It is also given that R is the midpoint of XC. Therefore, in triangle XYC, YR is a "sword line".
Therefore area of triangle YRC = half of area of triangle XYC = \(\frac{y}{8}\) square units.
Finally, it is given that S is the midpoint of YC. Therefore, RS is a "
sword line" in triangle YRC.
Therefore area of triangle RCS = half of area of triangle YRC = \(\frac{y}{16}\) square units.
Now statement 1 says that area of \(triangle ABX = 32\)
therefore, according to our nomenclature, \(\frac{y}{2} = 32\)
\(y = 64\)
\(\frac{y}{16} = 4\)
Therefore area of \(triangle YRC = 4\) square units.
Therefore statement 1 is sufficient.
Now we cannot determine anything with statement 2 unless we are given the vertex from which (or the side to which) the altitude is drawn.
Therefore statement 2 is not sufficient.
Since we arrive at a unique answer using Statement 1 alone, option A is the correct answer for this Data Sufficiency question.
Foot Note:The
sword line we used in this problem is widely referred to as the
median of a triangle.
The meaning of the word ‘median’ is clear from its name itself. The word "median" comes from the Latin root medius, which means ‘in between’. The English word ‘middle’ too comes from the same root. So, a median is the line that joins a vertex to the mid point of the opposite side of a triangle. (Obviously, every triangle will have 3 medians - one from each vertex).
However,
we do not need to know its name to understand how it works within the scope of the GMAT. This is the reason why I focused on first illustrating how that line works rather than telling its name.

Hope this helps.

- Krishna.



 85%
(hard)
85%
(hard)
 51%
(02:34)
wrong
51%
(02:34)
wrong  based on 4825
sessions
based on 4825
sessions