|
It is currently 26 May 2022, 06:58 |
Customized
for You
Track
Your Progress
Practice
Pays
08:30 AM PDT
-09:30 AM PDT
06:00 PM PDT
-07:00 PM PDT
08:30 AM PDT
-09:30 AM PDT
07:00 AM PDT
-09:00 AM PDT
07:00 AM PDT
-09:00 AM PDT
12:01 AM PDT
-11:59 PM PDT
08:00 PM EDT
-09:00 PM EDT
13 Jul 2020, 14:01
| FROM Magoosh Blog: GMAT Analytical Writing: All About the GMAT Essay and How to Prepare For It |
 Yup, the rumors are true: you’ll encounter a 30-minute GMAT analytical writing section on test day. But while analytical writing can seem tough at first, finding out exactly what’s expected and how to attack it for a maximum score will do a lot to make the GMAT essay feel manageable! In this post, we’ll take a look at what you need to know to master the GMAT AWA. Introduction to GMAT Analytical Writing[/*] [*]What to Expect for GMAT Analytical Writing[/*] [*]How to Approach the GMAT AWA (Strategy and Tips)[/*] [*]Breakdown by Section[/*] [*]Example GMAT Essays[/*] [*]Scoring for GMAT Analytical Writing[/*] [*]GMAT AWA and Business School[/*] [/list]   The first bullet point tells us: a good AWA essay is well-organized, has a natural flow from point to point, and is clear and unambiguous about what it is saying. Those are all important points to keep in mind. The second bullet point reminds us: what they present will be, in all likelihood, a flawed argument, but what you must create is a cogent and clear argument, and that will necessarily involve providing clear and relevant support. It’s not enough simply to assert something badly: you must provide justification for what you are saying. The final bullet points may appear enigmatic: “control the elements of standard written English.” What does that mean? Well, first of all, it means no grammar or syntax mistakes. It also means varying the sentence structure—some simple sentences (noun + verb), some with two independent clauses (noun + verb + and/but/or + noun + verb), some with dependent clauses, some with infinitive phrases, some with participial phrases, etc. Finally, it means choosing the right words and the right tone: the tone should be skeptical toward the prompt argument and persuasive toward the points you are making, but not arrogant or dogmatic in any way. The following paragraph always appears after the argument prompt. This is the real meat-and-potatoes of the AWA directions:  First of all, notice it give you one clear task: “Be sure to analyze the line of reasoning and the use of evidence in the argument.” Then, it lists several strategies that you might employ in your analysis. Don’t feel compelled to use every one of these in every AWA essay, though you should be using most of them in most essays. Recognizing assumptions is essential for the Critical Reasoning questions, and it will also serve you well on attacking the prompt argument in your AWA. [/*] [*]Know the Directions: This a matter not only of knowing what they say but also, more importantly, understanding the various options you have for analyzing the argument. This list of analytical strategies is always given in the paragraph that follows the prompt argument. It’s important to get familiar with this “analytical toolbox”, so it is yours to employ on test day.[/*] [*]Recognize the Common Flaw Patterns: GMAT AWA prompt arguments often contain one of six types of flaws. Learn to spot these patterns, so you are ready on test day.[/*] [*]Plan Before You Write: This is obvious to some test-takers. Your first task is to find objections to and flaws in the prompt argument. Create a list of flaws. Then, select the 2-4 of those that are most relevant, that would be the most persuasive talking points. Once you have your list of insightful flaws, then you are ready to write.[/*] [*]Use a Template: Many test takers find it helpful to have the basic structure of the AWA essay already planned out and practiced, so it’s just a matter of plugging in the specific details on test day. Here’s an example of a possible GMAT writing template. Feel free to adapt this template as is, modify it, or create one of your own.
In addition to variety in sentence structure, strive for variety in word choice. Of course, you will want to echo words that appear in the prompt argument. But in your own analysis, vary the descriptive words, never using the same word twice. Don’t say “weak … weak … weak” when you can say “unpersuasive … untenable … questionable.” Well-chosen synonyms can make an essay shine.[*]Avoid Common AWA Errors: There are a few common flaws that can pull your GMAT analytical writing score down. As you practice the AWA, make sure you avoid the following:
AWA brainstorming. As you brainstorm, list the argument’s flaws; then evaluate those flaws to find which objections are the strongest. Write an Introduction You don’t need to reinvent the wheel with each GMAT AWA introduction. Start by stating where the passage is from. Then, focus on two main tasks: summarizing the argument and stating why it’s flawed. Keep it short and sweet; three sentences are enough to get your main points set up! Construct Your Body Paragraphs These will make up the lion’s share of your essay, so you’ll spend most of your time writing body paragraphs. Here’s how to go about doing that:
First of all, keep in mind that you should not dwell in the conclusion. The heart of your essay, what really matters toward your score, is in the body paragraphs. These should be bulky and in-depth, but the conclusion should be short and to the point. Wrap things up in a timely manner so that you can get to the business of editing and revising your essay. To keep things manageable and short, don’t go into the details. You only need to recap the major problems in the argument. Sometimes it is enough to say that there are major problems in the argument. Ignore the desire to repeat all the main points that you covered in the body paragraphs. This will only take extra space and waste precious time. Finally, recommend a way to achieve the goal stated in the article. It is important to approach the analysis of the argument as an interested party. You don’t want to be wholly negative. For one, you will write a better analysis if you imagine yourself tied to the argument in some way, and two, the prompt asks you to strengthen the argument. Find some general evidence that will make the argument more convincing or make it irrefutable. Suggest a change so that the logic stands on firmer ground. examples of analytical questions for the GMAT, look no further! Once you’ve read few a through sample AWA prompts, read through the third prompt on page 31 of the PDF. Magoosh GMAT expert Mike McGarry has written a great GMAT AWA Example essay in response to this prompt, including analysis of why it works well and why it would receive a 6. GMAT AWA scoring rubric you can use for this purpose. But if you’re not certain about how your essays measure up to the GMAT scale, there are other ways to get your GMAT essay scored. These include GMAT Write, an official (paid) service from GMAC; friends; and forums. Take a look and see what option works best for you. recent evidence suggest that adcoms also rely on the IR score significantly more than the GMAT essay score. But while it’s true that, in your GMAT preparation, Quant and Verbal and even IR deserve more attention than the AWA, it’s also true you can’t completely neglect AWA. The difference between a 5 or 6 as your GMAT Analytic Writing score will not make or break a business school admission decision, but having an essay score below a 4 could hurt you. The purpose of the AWA is to see how well you write, how effectively you express yourself in written form. This is vital in the modern business world, where you may conduct extensive deals with folks you only know via email and online chatting. Some of your important contacts in your business career will know you primarily through your writing, and for some, your writing might be their first experience of you. You never get a second chance to make a first impression, and when this first impression is in written form, the professional importance of producing high-quality writing is clear. While you don’t need to write like Herman Melville, you need to be competent. A GMAT Analytic Writing score below 4 may cause business schools to question your competence. That’s why it’s important to have at least a decent showing in AWA. For Non-Native English Speakers In particular, if English is not your native language, I realize that this makes the AWA essay all the more challenging, but of course, a solid performance on the AWA by a non-native speaker would be a powerful testament to how well that student has learned English. Toward this end, non-native speakers should practice writing the AWA essay and try to get high-quality feedback on their essays. Devoting 30% or more of your available study time to AWA is likely unwise, but devoting 0% to AWA might also hurt you. Between those, erring on the low side would be appropriate. If, in a three-month span, you write half a dozen practice essays, and get generally positive feedback on them with respect to the GMAT standards, that should be plenty of preparation. Conclusion The GMAT analytical writing can feel like a slog when you first encounter it: it requires deep focus and analysis, and it’s not what most students have spent their prep time working on. But with a bit of preparation, your GMAT essays can take your admissions file to the next level by boosting your AWA score significantly! By including GMAT writing in your overall GMAT prep schedule, you’ll ensure that this section of the test doesn’t become a drag on your application—and helps, rather than hurts, your shot at your dream school. Good luck! The post GMAT Analytical Writing: All About the GMAT Essay and How to Prepare For It appeared first on Magoosh GMAT Blog. |
30 Jul 2020, 12:01
| FROM Magoosh Blog: GMAT Arithmetic 101 |
 The GMAT Quant section tests a variety of mathematical concepts, including algebra, geometry, and arithmetic. Generally speaking, the test-makers are not looking to trick or confuse you. Most GMAT math problems are rather straightforward. Read on to find out the specific arithmetic topics covered, tips for success, and plenty of practice problems! What kind of arithmetic is tested on the GMAT?[/*] [*]GMAT Arithmetic Tricks: 3 Tips for Success[/*] [*]GMAT Arithmetic Review: Practice Problems[/*] [*]Conclusion[/*] [/list] Arithmetic Operations[/*] [*]Number Properties[/*] [*]Fractions[/*] [*]Ratio and Proportions[/*] [*]Percents[/*] [*]Powers and Roots of Numbers[/*] [*]Statistics[/*] [*]Combinatorics (Counting Methods)[/*] [*]Discrete Probability[/*] [/list] Now let’s take a quick tour through these various areas. Some of the topics overlap a bit. And you may need to combine ideas to solve more challenging problems, but here are the basics. order of operations, or spotting common factors to cancel in complicated fractions. It’s important to have good number sense too. number properties. Primarily, we’re talking about properties of integers. So, be prepared to analyze evens and odds, consecutive integers and multiples, prime numbers, positives and negatives, and all the related concepts. For example, did you know that 1 is not a prime number? On the other hand, 0 is definitely an integer! fractions on the GMAT! GMAT Quantitative: Ratio and Proportions Understanding Percents on the GMAT[/*] [*]Percent Change Problems on the GMAT[/*] [*]GMAT Quant: Practice Problems with Percents[/*] [/list] Laws of Exponents and Roots will definitely help you to get through the GMAT Quantitative section. Here are a few links to get you started. But what about those “impossible” problems with huge tricky exponents, in which they ask for the units digit of the answer? Don’t fall into the trap of trying to work out the number exactly — that will eat up too much precious time. Instead, review these methods: GMAT Quant: Difficult Units Digits Questions. descriptive statistics and statistical significance. Often, the problems can be done without much of computation. For example, did you know that if you multiplied all of the data by the same number, \(k\), then the mean, median, mode, and standard deviation also gets multiplied by that same factor \(k\)? By contrast, adding the same number \(k\) to all of the data only changes the mean, median, and mode, while leaving the standard deviation the same!  Statistics make the world go ’round! (Image by Wynn Pointaux from Pixabay) factorials. Check out GMAT Permutations and Combinations for more! counting to geometric probability and problems based on dice, you have to be prepared for just about anything. But there are just a few fundamental concepts to keep in mind. The main idea behind probability is that it’s a fraction of the desired outcomes over the total number of outcomes. To get started, check out this article: GMAT Probability Rules. Also, you can expect probability to be a favorite topic for GMAT data sufficiency questions — for practice, see GMAT Data Sufficiency Practice Questions on Probability.  Click here for the video explanation from our GMAT product. [*]\(\dfrac{4^6-4^5}{3} = \) (A) \(\dfrac{4}{3}\) (B) \(4^{4/3}\) (C) \(4^4 – 4^{5/3}\) (D) \(4^5 – 4^4\) (E) \(4^5\) Show Answer The answer is E. Click here for the video explanation from our GMAT product. [*]\(\sqrt{81+81+81+81+81+81+81+81} = \) (A) \(18\sqrt{2}\) (B) \(36\sqrt{2}\) (C) 72 (D) \(162\sqrt{2}\) (E) 648 Show Answer The answer is A. Click here for the video explanation from our GMAT product. [*]If \(k\) is a positive integer, what is the smallest possible value of \(k\) such that \(1040k\) is the square of an integer? (A) 2 (B) 5 (C) 10 (D) 15 (E) 65 Show Answer The answer is E. Click here for the video explanation from our GMAT product. [*]If \(k\) is the greatest positive integer such that \(3^k\) is a divisor of \(15!\) then \(k = \) (A) 3 (B) 4 (C) 5 (D) 6 (E) 7 Show Answer The answer is D. Click here for the video explanation from our GMAT product. [*]A certain school district has specified 5 different novels and 4 different non-fiction books from which teachers can choose to assemble a summer reading list. Each summer reading list must have exactly 3 novels and 2 non-fiction books. How many different summer reading lists are possible? (A) 54 (B) 60 (C) 72 (D) 120 (E) 240 Show Answer The answer is B. Click here for the video explanation from our GMAT product. [/list] Data Sufficiency Questions For each of the below problems, choose one of the following: (A) Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient. (B) Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient. (C) BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient. (D) Each statement ALONE is sufficient to answer the question. (E) Statement 1 and 2 TOGETHER are NOT sufficient to answer the question. [*]Ann and Bob planted trees on Friday. What is the ratio of the number of trees that Bob planted to the number of trees that Ann planted? (1) Ann planted 20 trees more than Bob planted. (2) Ann planted 10 percent more trees than Bob planted. Show Answer The answer is (B) Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient. Click here for the video explanation from our GMAT product. [*]If \(P\) and \(Q\) are positive integers, and if \(P > 1\), does \(P = Q\)? (1) \(P\) is a factor of \(Q\) (2) \(P\) is a multiple of \(Q\) Show Answer The answer is (C) BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient. Click here for the video explanation from our GMAT product. [*]What is the value of \(x\)? (1) \( (x-5)^2 = 0 \) (2) \( (x-3)^2 = 4 \) Show Answer The answer is (A) Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient. Click here for the video explanation from our GMAT product. [*]A box contains only red chips, green chips, and blue chips. If a chip is randomly selected from the box, what is the probability that the chip is either red or green? (1) The probability of selecting a green chip is 1/3. (2) The probability of selecting a blue chip is 1/7. Show Answer The answer is (B) Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient. Click here for the video explanation from our GMAT product. [*]In a certain group, the average (arithmetic mean) age of the males is 28, and the average age of the females is 30. If there are 100 people in the group, how many of them are males? (1) The average age of all 100 people is 28.9 (2) There are 10 more males than there are females. Show Answer The answer is (D) Each statement ALONE is sufficient to answer the question. Click here for the video explanation from our GMAT product. [*]A certain aquarium holds three types of fish: angelfish, swordtails, and guppies. What is the ratio of the number of guppies to the number of angelfish? (1) There are 200 fish in the aquarium (2) 45 percent of the fish are swordtails, and there are twice as many swordtails as there are angelfish. Show Answer The answer is (B) Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient. Click here for the video explanation from our GMAT product. [/list] GMAT Arithmetic 101 appeared first on Magoosh GMAT Blog. |
31 Jul 2020, 13:01
| FROM Magoosh Blog: 20 GMAT Sentence Correction Practice Questions and Answers |
 Every time you put something into writing in a professional setting, it should represent you at your very best—and an important part of that is correct grammar. That’s why business schools care about it, which is why the GMAT tests it. The primary vehicle for testing grammar on the GMAT is the Sentence Correction questions. Keep reading to see what is tested on GMAT Sentence Correction, practice questions for SC, and tips for success. ? What is GMAT Sentence Correction?[/*] [*]How can I do well on SC?[/*] [*]How to Master Sentence Correction on GMAT [*]GMAT Sentence Correction Practice Questions with Explanations[/list] GMAT Sentence Correction Strategies. While you’re thinking about strategy, here are some tips on how to ace GMAT sentence correction! GMAT Sentence Correction Practice Questions is an excellent resource. It compiles links to other blog posts, listed by the rule that they have to do with. So, if you wanted to learn about gerunds and gerund phrases, or when to use like vs. as, you can go to a post that focuses on that rule with examples. In many ways, SC improvement takes time. You have to learn and re-learn grammar and style rules. This takes time, so be patient with yourself. Use the lesson videos, and make sure to learn from your practice. Also, your process of elimination skills need sharpening and training. The GMAT is a rapid and tricky test, and the more organized and purposeful prep that you do, the more likely it is that you’ll see an increase in your practice scores. GMAT prep and are a good sample of the different sorts of questions you’re likely to see on your exam. Plenty of different grammar and style rule violations, problems with the structure and logical flow, and some examples of issues with idioms and phrasing.
The post 20 GMAT Sentence Correction Practice Questions and Answers appeared first on Magoosh GMAT Blog. |
31 Jul 2020, 19:00
| FROM Magoosh Blog: GMAT Sentence Correction with 20 Practice Questions and Answers |
|
Every time you put something into writing in a professional setting, it should represent you at your very best—and an important part of that is correct grammar. That’s why business schools care about it, which is why the GMAT tests it. The primary vehicle for testing grammar on the GMAT is the Sentence Correction questions. Keep reading to see what is tested on GMAT Sentence Correction, practice questions for SC, and tips for success. ? What is GMAT Sentence Correction?[/*] [*]How can I do well on SC?[/*] [*]How to Master Sentence Correction on GMAT [*]GMAT Sentence Correction Practice Questions with Explanations[/list] GMAT Sentence Correction Strategies. While you’re thinking about strategy, here are some tips on how to ace GMAT sentence correction! GMAT Sentence Correction Practice Questions is an excellent resource. It compiles links to other blog posts, listed by the rule that they have to do with. So, if you wanted to learn about gerunds and gerund phrases, or when to use like vs. as, you can go to a post that focuses on that rule with examples. In many ways, SC improvement takes time. You have to learn and re-learn grammar and style rules. This takes time, so be patient with yourself. Use the lesson videos, and make sure to learn from your practice. Also, your process of elimination skills need sharpening and training. The GMAT is a rapid and tricky test, and the more organized and purposeful prep that you do, the more likely it is that you’ll see an increase in your practice scores. GMAT prep and are a good sample of the different sorts of questions you’re likely to see on your exam. Plenty of different grammar and style rule violations, problems with the structure and logical flow, and some examples of issues with idioms and phrasing.
The post GMAT Sentence Correction with 20 Practice Questions and Answers appeared first on Magoosh GMAT Blog. |
26 Aug 2020, 20:01
| FROM Magoosh Blog: Integrated Reasoning on the GMAT: The Complete Guide |
 If you’re sitting down to your first GMAT Integrated Reasoning section, you might not know what to think! You’ll have 30 minutes to answer 12 Integrated Reasoning GMAT questions involving a ton of data analysis, critical thinking, and quantitative reasoning. But by preparing early—and thoroughly!—you’ll be able to get the Integrated Reasoning GMAT score that you want on test day. What is GMAT Integrated Reasoning? The GMAT Integrated Reasoning section tests your quant-based and verbal-based reasoning in 4 parts: multi-source reasoning, table analysis, two-part analysis, and graphics interpretation. Essentially, the GMAT IR section is testing for your data analysis skills. The big question for many students: just what is the GMAT IR score importance? IR is relatively important (and increasingly so!), so it’s vital not to ignore it! Overall, you can expect to see 12 questions in 30 minutes. It’s not quite as simple as it sounds, though: each graph or prompt will have multiple questions. In addition, you’ll have to answer a question before you can move on—and you can’t go back to a question once you’ve answered it.  Check out this video of Magoosh’s Introduction to Integrated Reasoning lesson! Integrated Reasoning Question Types on the GMAT Multi-Source Reasoning Multi-source reasoning questions show you a split screen: on the left, you’ll have three clickable cards, each with a piece of information that will help you answer a particular question, and which you can only see one of at a time. The questions are either standard five-choice multiple choice or multiple dichotomous choice. You’ll have two answer choices (e.g. “true/false”) for each part of a three-part question. For more sample multi-source reasoning problems, click here! Table Analysis Table analysis questions give you a sortable table of numbers. These are accompanied by multiple dichotomous choice questions, in which you have two answer choices (e.g. “true/false”) for each part of a three-part question. Check out a sample table analysis problem! Graphics Interpretation For graphics interpretation questions, you’ll receive some visual information in the form of a chart or a graph, then questions containing two drop-down menus each. These menus will have you fill in blanks within a sentence according to the data shown in the visual. Check out more sample graphics interpretation problems! Two-Part Analysis Two-part analysis questions give you a large prompt, followed by a question-and-answer table. You will fill out the answers for each of two questions, which can vary; they may be partially or completely related, but they will always be interdependent. Check out a sample two-part analysis problem! Strategies for Getting a Good Integrated Reasoning GMAT Score Getting a good Integrated Reasoning GMAT score can be tricky—not least of all because a lot of people aren’t sure what a good IR score is! Unlike the total GMAT score, which is scored between 200 and 800, IR is scored between 1 and 8. Most people would consider a good score to be above the 50th percentile—in other words, better than half of test-takers’ scores. For IR, this is a 5 or higher. So how do you get that good score of 5+ on GMAT IR? Here are a few keys to succeeding:
Need Integrated Reasoning GMAT practice? You’re not alone! That’s why Magoosh is excited to present you with the ultimate GMAT Integrated Reasoning eBook: Magoosh’s Complete Guide to GMAT Integrated Reasoning! Here, you’ll find detailed explanations and tips for each IR question type, as well as practice witin each area.   Still want more? You can find Magoosh’s guide to the official GMAT Integrated Reasoning practice here! A Final Note GMAT Integrated Reasoning questions are designed to throw a lot of data at you, fast. And while a lot of test-takers will let that throw them off their game, you can ensure that you’re all set for test day by familiarizing yourself with these question types and practicing, practicing, practicing! The more used to the question types you are, the easier your test day experience will be. And the GMAT IR prep tools in this post will help you get there. Good luck! The post Integrated Reasoning on the GMAT: The Complete Guide appeared first on Magoosh GMAT Blog. |
28 Sep 2020, 18:01
| FROM Magoosh Blog: GMAT Word Problems: Introduction, Strategies, and Practice Questions |
 You may love GMAT word problems or you may hate them, but you can’t get around them if you want to ace the GMAT Quant section. No matter what your feelings are about this problem type, though, Magoosh’s experts have put together everything you need to know (and practice!) GMAT word problems in order to master them before test day. What to Expect from GMAT Word Problems[/*] [*]Strategy Guide: What’s the Trick to Mastering GMAT Word Problems?
GMAT Quant section. How much of the GMAT is word problems? Within the Quant section, actually a whole lot! A study of official GMAT questions from actual tests show that word problems account for 58.2% of all GMAT math questions. 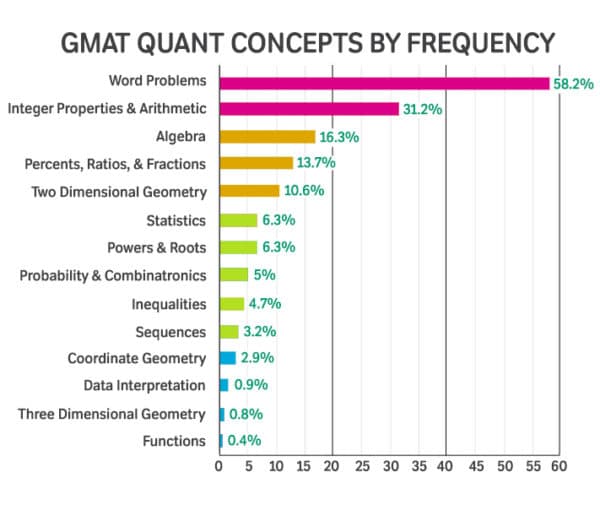 In other words, test-takers should anticipate a word problem cropping up (on average) in three out of every five questions you’ll see in Quant. Because of GMAT word problems’ prevalence, you can expect to see both Data Sufficiency and Problem Solving questions in this format. The question format and answer choices may look different, but the basic premise will be the same. You may be feeling the pressure, but hang in there! If you’re worried about how to master word problems on the GMAT, keep reading for our GMAT Word Problems strategy guide. Variables in GMAT Answer Choices: 2 Approaches. tips for plugging in numbers that you should use! Here’s a quick summary of how to quick the best numbers for a particular problem:
Click here for a video answer and explanation to GMAT Word Problem 1![/b] Click here for a text answer and explanation to GMAT Word Problem 1! Our task is to determine the ratio of Bob’s trees to Ann’s trees. Let’s label these numbers of trees with variables: Bob’s trees→B, Ann’s trees→A With these variables, we can express the ratio we want to determine: \(B/A\) =? Statement 1: Ann planted 20 trees more than Bob planted. Let’s translate this into an equation using A and B: \( A=B+20 \) Now we can substitute this into our ratio, replacing A: \(B/A\) = \( B/(B+20) \) No matter what simplifications we make, we cannot find a numerical value for this fraction. We would need a value for B. We cannot determine the ratio. Statement 1 by itself is not sufficient. Statement 2: Ann planted 10 percent more trees than Bob planted. Let’s translate this into an equation using A and B: \(A=1.10 x B \) Again, let’s substitute this in for A in our ratio: \(B/A\) = \( B/(1.10B) \) = \(1/1.1 \) We found a value for the ratio of Bob’s trees to Ann’s trees. Statement 2 alone is sufficient. [*]The Townville museum was open for 7 consecutive days. If the number of visitors each day was 3 greater than the previous day, how many visitors were there on the first day? (1) There were a total of 126 visitors for the 7 days. (2) The number of visitors on the seventh day was three times the number of visitors on the first day. [/list] A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient. B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient. C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient. D. Each statement ALONE is sufficient to answer the question. E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question. Click here for a video answer and explanation to GMAT Word Problem 2! Click here for a text answer and explanation to GMAT Word Problem 2! If x is the number of visitors on the first day, then: x = # of visitors on the 1st day x + 3 = # of visitors on the 2nd day x + 6 = # of visitors on the 3rd day x + 9 = # of visitors on the 4th day x + 12 = # of visitors on the 5th day x + 15 = # of visitors on the 6th day x + 18 = # of visitors on the 7th day 1) Adding up the number of visitors gives us: x + (x + 3) + (x + 9) + (x + 12) + (x + 15) + (x + 18) = 126 We could simplify and solve this for x. So Statement 1 is sufficient. 2) x + 18 = 3x Again, we can simplify this and solve for x. So Statement 2 is sufficient. Answer: (D) [*]Two teachers, Ms. Ames and Mr. Betancourt, each had N cookies. Ms. Ames was able to give the same number of cookies to each one of her 24 students, with none left over. Mr. Betancourt was also able to give the same number of cookies to each one of his 18 students, with none left over. If N > 0, what is the value of N? (1) N<100 (2) N > 50 [/list] A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient. B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient. C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient. D. Each statement ALONE is sufficient to answer the question. E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question. Click here for a video answer and explanation to GMAT Word Problem 3! Click here for a text answer and explanation to GMAT Word Problem 3! This question is really about common multiples and the LCM (note that it is different than finding the set of all multiples, though!). If Ms. Ames can give each of her 24 students k cookies, so that they all get the same and none are left over, then 24k = N. Similarly, in Mr. Betancourt’s class, 18s = N. What are the common multiples of 18 and 24? 18 = 2×9 = 2×3×3 = 6×3 24 = 3×8 = 2×2×2×3 = 6×4 From the prime factorizations, we see that GCF = 6, so the LCM is LCM = 6×3×4 = 72 and all other common multiples of 18 and 24 are the multiples of 72: {72, 144, 216, 288, 360, …} Statement #1: if N<100, the only possibility is N = 72. This statement, alone and by itself, is sufficient. Statement #2: if N > 50, then N could be 72, or 144, or 216, or etc. Many possibilities. This statement, alone and by itself, is not sufficient. Answer = (A) [*]A certain zoo has mammals and reptiles and birds, and no other animals. The ratio of mammals to reptiles to birds is 11:8:5. How many birds are in the zoo? (1) there are twelve more mammals in the zoo than there are reptiles (2) if the zoo acquired 16 more mammals, the ratio of mammals to birds would be 3:1 [/list] A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient. B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient. C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient. D. Each statement ALONE is sufficient to answer the question. E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question. Click here for a video answer and explanation to GMAT Word Problem 4! Click here for a text answer and explanation to GMAT Word Problem 4! A short way to do this problem. The prompt gives us ratio information. Each statement gives use some kind of count information, so each must be sufficient on its own. From that alone, we can conclude: answer = D. This is all we have to do for Data Sufficiency. Here are the details, if you would like to see them. Statement (1): there are twelve more mammals in the zoo than there are reptiles From the ratio in the prompt, we know mammals are 11 “parts” and reptiles are 8 “parts”, so mammals have three more “parts” than do reptiles. If this difference of three “parts” consists of 12 mammals, that must mean there are four animals in each “part.” We have five bird “parts”, and if each counts as four animals, that’s 5*4 = 20 birds. This statement, alone and by itself, is sufficient. Statement (2): if the zoo acquired 16 more mammals, the ratio of mammals to birds would be 3:1 Let’s say there are x animals in a “part”—this means there are currently 11x mammals and 5x birds. Suppose we add 16 mammals. Then the ratio of (11x + 16) mammals to 5x birds is 3:1. (11x + 16)/(5x) = 3/1 = 3 11x + 16 = 3*(5x) = 15x 16 = 15x – 11x 16 = 4x 4 = x So there are four animals in a “part”. The birds have five parts, 5x, so that’s 20 birds. This statement, alone and by itself, is sufficient. Both statements are sufficient. Answer = D. average speed to total distance traveled, from total time to total amount. The key now is to put them into practice. Jot down these techniques or bookmark this post so you can come back as you continue your practice with GMAT word problems. You can also check out our posts on compound interest and Venn diagrams for more practice with GMAT word problems. Good luck! This post was written with contributions from our Magoosh content creator, Rachel Kapelke-Dale. The post GMAT Word Problems: Introduction, Strategies, and Practice Questions appeared first on Magoosh GMAT Blog. |
05 Oct 2020, 09:01
| FROM Magoosh Blog: GMAT Error Log: The Key to GMAT Success (Free Template Included) |
 Your GMAT journey will be both challenging and rewarding. You will have highs and lows. There will be days that will build your confidence and then other days you will want to forget about completely. We have all had those days: you are studying and you feel like you can’t get any question right. But before you crumble up that paper, wipe clean that dry erase board, or power down that computer, STOP! Document your struggles and capture that data! Why Keeping an Error Log is So Important Our mistakes are chock full of information about our test taking abilities, strategies, and more importantly, our habits. Whether you’re GMAT studying for the first time or preparing for a retake, a critical look at how we approach, solve, and check our work will not only direct us to which areas we should study next, but will make us conscious about the bad habits we exhibit every time we attempt a GMAT problem.  We are always told to review our questions after we complete practice problems and the best way to advance your skills is by using a GMAT Error Log! I know what you’re thinking: not another GMAT wonder tool you have to buy to achieve your goal score. We get it. The GMAT is not only taxing on you mentally, physically, and socially (no one wants to hang out with the guy with Critical Reasoning flashcards at the party), but the GMAT is also COSTLY! That’s the beauty of the GMAT Error Log—it’s a completely free tool! Even better, keep reading and I will share with you a template I use to save you time on finding one online. Yes, the power of self evaluating your GMAT progress can be yours with a few clicks of a mouse! How to Use an Error Log GMAT prep is broken down into three parts: Content, Problem Solving, & Testing. What I have seen that keeps test-takers from earning their top score is that they haven’t spent enough time in the Problem Solving stage. Test-takers would read 100% of the material and complete 4 to 5 practice CAT exams, but would only successfully complete 20-30% of all the questions on the Magoosh platform and even less when it comes to the Official Guide. Knowing the ratios of a 30-60-90 triangle, how to FOIL, or what is a noun is important, but you must drill these topics in various various ways to really understand these concepts and how to answer these questions on the exam. Taking CAT exams in isolation will not improve your score. It is in careful review and reflection is where you will develop skills and earn points. CAT exams are a major time investment and are extremely valuable, so you don’t want to waste too much time to only answer 30 or more random questions. What I have seen successful test-takers do is create mini problems sets (5, 8, 10, or 16 questions) and use those as a sample test to gauge their skill set. In these practice problems is where the GMAT Error Log shines!  Let’s say each day for a week, you complete 10 to 20 random problems of various question types and difficulties. You are bound to miss a few questions. What most people do when they get a question wrong is read the explanation, say “oh I got it,” and move on. Here is where you leverage the GMAT Error Log. Not only will you read the explanation, you will also input the question you got wrong in the Error Log, what you did wrong, and what you will do differently next time. This seems like a small task today, but in the beginning, it can feel very daunting. After about 20 or so questions, though, you will get into the habit of updating your error log and begin to see the fruits of your labor. Leading up to a test day, a great Error Log can be a great review tool right before a CAT exam. When I work with my test-takers I teach them how to build a detailed Error Log with great care because it is those careless errors or habits that are written in the Error Log that jumps your GMAT score from a 620 to 650 or 690 to that 700. How to Structure Your GMAT Log Your Error Log does not need to have many bells and whistles. It doesn’t need to be something with macros and automated graphic generators. It doesn’t have to be a spreadsheet or digital at all. I actually keep two logs – an old school black and white marble notebook and a digital copy. The Error Log just has to fit your method of note-taking and meet your dedication to the process. Error Logs lose value when they are not updated. You only get out of the Error Log what you put in. I can never guarantee your score to improve, but I can say that having a running list of all your mistakes can help prevent you from making them again. Here is the key information you want to have in any GMAT Error Log:
This sounds extremely simple, because it is – the challenging part is sticking to the habit. After a few weeks, you will have an error log that you will cherish and will be excited to fill it up. So go out there and make some GMAT mistakes! I am here to help you—feel free to comment below and include a copy of your own error log and I will provide you some feedback and additional examples. The post GMAT Error Log: The Key to GMAT Success (Free Template Included) appeared first on Magoosh GMAT Blog. |
30 Oct 2020, 19:01
| FROM Magoosh Blog: Build Your Own GMAT Study Schedule |
 You may have heard that studying for the GMAT is similar to preparing for a marathon. Not many people could run 26.2 miles (42.195 kilometers) without months of preparation! Though you probably won’t be as sweaty as you would be if you were to run for hours, you’ll still need endurance, speed, and strong mental skills to get through the GMAT with the score you deserve. Now, if you’re planning to run a marathon, your schedule is easy to fill out — It’s running on Monday, Tuesday probably some running, and then more running on Wednesday, Thursday, and so on. Not so simple with the GMAT! On your big day, you need to be prepared to use dozens of different math and grammar rules, track the meaning of several thousand words of text, and solve math problems with no calculator, all while going really fast and not making any mistakes. So more like a three-legged hot yoga CrossFit marathon. So what’s your plan? If you’re looking for some help deciding what to do each Monday, Tuesday, and Wednesday to be ready for the unique challenges of the GMAT, you’ve found it! Once you have a goal in mind, and you’ve gathered some helpful resources, it’s time to start building your own GMAT study schedule. Stay motivated — know your goals What are your hopes and dreams? Who are you and who do you aspire to be? Sorry, I didn’t mean to get too personal, but some reflecting on your reasons for studying for a 3+ hour exam that costs hundreds of dollars and determines a big part of your future is a great place to start! If you need some ideas, consider your short term vs. your long term goals. Your short term goal might be to take the GMAT in 3 months and score 750, but your long term goal might be to get into a top MBA program and then conquer the world of finance (or maybe just prove to your old calculus professor that you are worth more than the Σ of your parts). I recommend writing down your goals and keeping them somewhere visible — on the fridge, the mirror, or out on your desk. When you’re feeling discouraged or especially tired, look back to your goals to reinvigorate you and remind you of why you’re putting yourself through this. Before you get started Before you start building your own GMAT study schedule, you’ll need to get squared away with a couple initial steps. The schedule builder will use a little info to guide you to a recommended study schedule template. Most importantly, it wants to know the results from your diagnostic tests. If you haven’t had all that fun yet, take about an hour and complete both the quantitative and verbal diagnostic tests. Then head back here and you’ll be ready to go. Build your custom GMAT study schedule After you’ve completed your diagnostic, just take this brief quiz and then we’ll recommend a template of your study schedule to get started with! powered by Typeform The post Build Your Own GMAT Study Schedule appeared first on Magoosh GMAT Blog. |
24 Nov 2020, 18:01
| FROM Magoosh Blog: How to Solve GMAT Motion Problems |
 Word Problems make up a majority of the quantitative section of the GMAT (almost 60 percent). Of the word problems they’ll face, students tend to need the most help with GMAT motion problems. This type of problem centers around the “dust” formula, which is short for Distance equals Speed multiplied by Time, or \(\text{D}\times\text{S}=\text{T}\). But there are many varieties of motion problem, and we will discuss techniques for each of them. At the end of this article, you’ll also find motion word problems with solutions for you to test your knowledge! The Distance Equation[/*] [*]Multi-Segment Motion Problems[/*] [*]Average Speed[/*] [*]Multiple Traveler Questions[/*] [*]Shrinking and Expanding Gaps[/*] [*]Data Sufficiency[/*] [*]GMAT Motion Problems Review: Practice Problems[/*] [/list] Distance equals Speed multiplied by Time, or \(\text{D}\times\text{S}=\text{T}\). If you learn this basic equation well, you’ll be able to dust your math troubles away! (Insert rimshot.) We can rearrange this formula to determine that Speed is equal to Distance divided by Time, and that Time is equal to Distance divided by Speed. Distance is the measurement of how far apart objects, people, or points are. Speed is the rate at which someone or something is traveling. Time is how long it takes to travel. Let’s demonstrate this. Walking at a constant rate of 160 meters per hour, Monroe can cross a bridge in 2 hours. What is the length of the bridge? Here, the length of the bridge is the distance Monroe must cross. Using Distance equals Speed multiplied by Time, we get: \((160\;\text{meters per hour})\times(2\;\text{hours})=320\;\text{meters}\) Seems simple enough so far, right? Let’s check out a few more GMAT motion problems. Speed is equal to Distance divided by Time. Let’s take that a step further and talk about average speed. Average speed is defined as total distance traveled divided by the total time period spent traveling. This means that if you have a trip with multiple segments, you’ll want to take the sum of the distances of each segment and divide that by the sum of the times of each segment. Average speed captures the constant speed needed to travel the total distance in the total time. Let’s demonstrate this. Koki drove 16 miles in 10 minutes, and then drove an additional 6 miles in 5 minutes. What is Koki’s average speed for the entire trip in miles per hour? Click here for the answer and explanation Well, average speed is the total distance divided by the total time. \(\text{D}_\text{Total}=16\;\text{miles}+6\;\text{miles}=22\;\text{miles}\) \(\text{T}_\text{Total}=10\;\text{minutes}+5\;\text{minutes}=15\;\text{minutes}\) \(\text{S}_\text{Average}=\frac{\text{D}_\text{Total}}{\text{T}_\text{Total}}\) \(\text{S}_\text{Average}=\frac{22\;\text{miles}}{15\;\text{minutes}}\times\frac{60\;\text{minutes}}{1\;\text{hour}}=88\;\text{miles per hour}\) That’s straightforward enough, but what if we are not given any distances or times? It is possible to solve an average speed problem, even if all you are given are the different speeds in each segment of the trip. You might then think that average speed would just be the average of all of the speeds, but that is not correct. Let’s say that Nathaniel drove from Gwenville to Samton at an average speed of 24 miles per hour. He then drove the same route on the return trip back from Samton to Gwenville at an average speed of 36 miles per hour. If you were asked to find Nathaniel’s average speed, it would not just be 30 miles per hour (the average of 24 and 36). Click here to work through this problem To see this, let’s go back to our MVP dust formula. Since there are two legs of the trip, we will have two equations. D1, S1, T1; D2, S2, T2. Because Nathaniel’s trip is a round trip, we can assume that D1and D2 are the same, so we will set both of them equal to D. \(\text{D}_1=\text{D}\\\text{S}_1=24\;\text{miles per hour}\\\text{T}_1=\frac{D}{24\;\text{miles per hour}}\) \(\text{D}_2=\text{D}\\\text{S}_2=36\;\text{miles per hour}\\\text{T}_2=\frac{D}{36\;\text{miles per hour}}\) \(\text{D}_\text{Total}=\text{2D}\) \(\text{T}_\text{Total}=\frac{D}{24\;\text{miles per hour}}+\frac{D}{36\;\text{miles per hour}}\) \(\text{S}_\text{Average}=\frac{\text{D}_\text{Total}}{\text{T}_\text{Total}}\) \(\text{S}_\text{Average}=\frac{\text{2D}}{\frac{D}{24\;\text{miles per hour}}+\frac{D}{36\;\text{miles per hour}}}\) We can factor a D out of this fraction. \(\text{S}_\text{Average}=\frac{2}{\frac{1}{24}+\frac{1}{36}}\;\text{miles per hour}\) We can find a common denominator between 24 and 36. \(\text{S}_\text{Average}=\frac{2}{\frac{3}{72}+\frac{2}{72}}\;\text{miles per hour}\) \(\text{S}_\text{Average}=\frac{2}{\frac{5}{72}}\;\text{miles per hour}=\frac{2}{1}\times\frac{72}{5}=\frac{144}{5}\;\text{miles per hour}=28.8\;\text{miles per hour}\) In summary, whenever you want to find the average speed of a round trip, and you are given the two segment speeds, you can put it in the form \(\text{S}_\text{Average}=\frac{\text{2}}{\frac{1}{\text{S}_1}+\frac{1}{\text{S}_2}}\). You can also use this formula to find one of the segment speeds, given the other segment speed and the average speed. diagram. Let’s say that a car and truck are moving in the same direction on the same highway. The truck is moving at 50 miles an hour, and the car is traveling at a constant speed. At 3 pm, the car is 30 miles behind the truck and at 4:30 pm, the car overtakes and passes the truck. What is the speed of the car? Click here for the answer and explanation The car and truck are moving in the same direction, and the car is gaining on the truck. This means that the gap between the vehicles is shrinking and that the gap rate is the difference of the two vehicles’ respective speeds. \(\text{S}_\text{G}=\text{S}_\text{C}-\text{S}_\text{T}\) The distance of the gap is initially 30 miles. \(\text{D}=30\;\text{miles}\) The time frame we are given for the closing of the gap is from 3 pm to 4:30 pm. \(\text{T}=1.5\;\text{hours}=\frac{3}{2}\;\text{hours}\) \(\text{S}_\text{G}=\frac{\text{D}}{\text{T}}\) \(\text{S}_\text{G}=\frac{30\;\text{miles}}{\frac{3}{2}\;\text{hours}}=30\times\frac{2}{3}=20\;\text{miles per hour}\) \(20\;\text{miles per hour}=\text{S}_\text{C}-50\;\text{miles per hour}\) \(20\;\text{miles per hour}+50\;\text{miles per hour}=\text{S}_\text{C}=70\;\text{miles per hour}\) data sufficiency question from Magoosh, then review the video explanation.[/*] [/list] Let us know how you did on these practice questions in the comments below. If you’re looking for more GMAT motion problems, try out one of Magoosh’s GMAT plans, which comes with practice tests, video lessons, and study schedules. Good luck! The post How to Solve GMAT Motion Problems appeared first on Magoosh Blog — GMAT® Exam. |
25 Nov 2020, 15:01
| FROM Magoosh Blog: How to Solve GMAT Motion Problems |
|
Word Problems make up a majority of the quantitative section of the GMAT (almost 60 percent). Of the word problems they’ll face, students tend to need the most help with GMAT motion problems. This type of problem centers around the “dust” formula, which is short for Distance equals Speed multiplied by Time, or \(\text{D}\times\text{S}=\text{T}\). But there are many varieties of motion problem, and we will discuss techniques for each of them. At the end of this article, you’ll also find motion word problems with solutions for you to test your knowledge! The Distance Equation[/*] [*]Multi-Segment Motion Problems[/*] [*]Average Speed[/*] [*]Multiple Traveler Questions[/*] [*]Shrinking and Expanding Gaps[/*] [*]Data Sufficiency[/*] [*]GMAT Motion Problems Review: Practice Problems[/*] [/list] Distance equals Speed multiplied by Time, or \(\text{D}\times\text{S}=\text{T}\). If you learn this basic equation well, you’ll be able to dust your math troubles away! (Insert rimshot.) We can rearrange this formula to determine that Speed is equal to Distance divided by Time, and that Time is equal to Distance divided by Speed. Distance is the measurement of how far apart objects, people, or points are. Speed is the rate at which someone or something is traveling. Time is how long it takes to travel. Let’s demonstrate this. Walking at a constant rate of 160 meters per hour, Monroe can cross a bridge in 2 hours. What is the length of the bridge? Here, the length of the bridge is the distance Monroe must cross. Using Distance equals Speed multiplied by Time, we get: \((160\;\text{meters per hour})\times(2\;\text{hours})=320\;\text{meters}\) Seems simple enough so far, right? Let’s check out a few more GMAT motion problems. Speed is equal to Distance divided by Time. Let’s take that a step further and talk about average speed. Average speed is defined as total distance traveled divided by the total time period spent traveling. This means that if you have a trip with multiple segments, you’ll want to take the sum of the distances of each segment and divide that by the sum of the times of each segment. Average speed captures the constant speed needed to travel the total distance in the total time. Let’s demonstrate this. Koki drove 16 miles in 10 minutes, and then drove an additional 6 miles in 5 minutes. What is Koki’s average speed for the entire trip in miles per hour? Click here for the answer and explanation Well, average speed is the total distance divided by the total time. \(\text{D}_\text{Total}=16\;\text{miles}+6\;\text{miles}=22\;\text{miles}\) \(\text{T}_\text{Total}=10\;\text{minutes}+5\;\text{minutes}=15\;\text{minutes}\) \(\text{S}_\text{Average}=\frac{\text{D}_\text{Total}}{\text{T}_\text{Total}}\) \(\text{S}_\text{Average}=\frac{22\;\text{miles}}{15\;\text{minutes}}\times\frac{60\;\text{minutes}}{1\;\text{hour}}=88\;\text{miles per hour}\) That’s straightforward enough, but what if we are not given any distances or times? It is possible to solve an average speed problem, even if all you are given are the different speeds in each segment of the trip. You might then think that average speed would just be the average of all of the speeds, but that is not correct. Let’s say that Nathaniel drove from Gwenville to Samton at an average speed of 24 miles per hour. He then drove the same route on the return trip back from Samton to Gwenville at an average speed of 36 miles per hour. If you were asked to find Nathaniel’s average speed, it would not just be 30 miles per hour (the average of 24 and 36). Click here to work through this problem To see this, let’s go back to our MVP dust formula. Since there are two legs of the trip, we will have two equations. D1, S1, T1; D2, S2, T2. Because Nathaniel’s trip is a round trip, we can assume that D1and D2 are the same, so we will set both of them equal to D. \(\text{D}_1=\text{D}\\\text{S}_1=24\;\text{miles per hour}\\\text{T}_1=\frac{D}{24\;\text{miles per hour}}\) \(\text{D}_2=\text{D}\\\text{S}_2=36\;\text{miles per hour}\\\text{T}_2=\frac{D}{36\;\text{miles per hour}}\) \(\text{D}_\text{Total}=\text{2D}\) \(\text{T}_\text{Total}=\frac{D}{24\;\text{miles per hour}}+\frac{D}{36\;\text{miles per hour}}\) \(\text{S}_\text{Average}=\frac{\text{D}_\text{Total}}{\text{T}_\text{Total}}\) \(\text{S}_\text{Average}=\frac{\text{2D}}{\frac{D}{24\;\text{miles per hour}}+\frac{D}{36\;\text{miles per hour}}}\) We can factor a D out of this fraction. \(\text{S}_\text{Average}=\frac{2}{\frac{1}{24}+\frac{1}{36}}\;\text{miles per hour}\) We can find a common denominator between 24 and 36. \(\text{S}_\text{Average}=\frac{2}{\frac{3}{72}+\frac{2}{72}}\;\text{miles per hour}\) \(\text{S}_\text{Average}=\frac{2}{\frac{5}{72}}\;\text{miles per hour}=\frac{2}{1}\times\frac{72}{5}=\frac{144}{5}\;\text{miles per hour}=28.8\;\text{miles per hour}\) In summary, whenever you want to find the average speed of a round trip, and you are given the two segment speeds, you can put it in the form \(\text{S}_\text{Average}=\frac{\text{2}}{\frac{1}{\text{S}_1}+\frac{1}{\text{S}_2}}\). You can also use this formula to find one of the segment speeds, given the other segment speed and the average speed. diagram. Let’s say that a car and truck are moving in the same direction on the same highway. The truck is moving at 50 miles an hour, and the car is traveling at a constant speed. At 3 pm, the car is 30 miles behind the truck and at 4:30 pm, the car overtakes and passes the truck. What is the speed of the car? Click here for the answer and explanation The car and truck are moving in the same direction, and the car is gaining on the truck. This means that the gap between the vehicles is shrinking and that the gap rate is the difference of the two vehicles’ respective speeds. \(\text{S}_\text{G}=\text{S}_\text{C}-\text{S}_\text{T}\) The distance of the gap is initially 30 miles. \(\text{D}=30\;\text{miles}\) The time frame we are given for the closing of the gap is from 3 pm to 4:30 pm. \(\text{T}=1.5\;\text{hours}=\frac{3}{2}\;\text{hours}\) \(\text{S}_\text{G}=\frac{\text{D}}{\text{T}}\) \(\text{S}_\text{G}=\frac{30\;\text{miles}}{\frac{3}{2}\;\text{hours}}=30\times\frac{2}{3}=20\;\text{miles per hour}\) \(20\;\text{miles per hour}=\text{S}_\text{C}-50\;\text{miles per hour}\) \(20\;\text{miles per hour}+50\;\text{miles per hour}=\text{S}_\text{C}=70\;\text{miles per hour}\) data sufficiency question from Magoosh, then review the video explanation.[/*] [/list] Let us know how you did on these practice questions in the comments below. If you’re looking for more GMAT motion problems, try out one of Magoosh’s GMAT plans, which comes with practice tests, video lessons, and study schedules. Good luck! The post How to Solve GMAT Motion Problems appeared first on Magoosh Blog — GMAT® Exam. |
24 Dec 2020, 17:01
| FROM Magoosh Blog: Everything You Need to Know about Getting an MBA |
 An MBA, or a “Masters of Business Administration,” is a postgraduate degree achieved after an MBA candidate successfully goes through a business-focused program, usually lasting 1 to 2 years, and can be full-time or part-time. MBA programs are intended to better prepare you for business management skills and to make graduates more competitive in applying for leadership roles, or to crack into popular and high-paying industries, like tech, high-finance, and consulting. Check out our answers to frequently asked questions about the MBA below! What Is an MBA? [*]What Are the Benefits of an MBA?[*]What Do MBAs Cost?[*]How Hard Is an MBA?[*]Who Is an Ideal MBA Candidate?[*]How Do I Apply for MBA Programs?[*]When Should I Start Applying for an MBA?[/list]  full-time and part-time MBA as both went through the same academic rigors. Online MBA Programs This is the broadest category here, as “online MBAs” could very well be EMBAs, full-time or part-time. Generally, the feature is in the name: it’s online, rather than in-person, but there are some hybrids. Scholarships, as noted above, are more plentiful for full-time in-person programs. Your mileage here will vary depending on the university, as many programs have deep wells of experience in facilitating connections and learning online, but others are a little newer to the scene and adapting to the increasing trend to move online.
Joint Degree Programs Best for those who have a more defined post-MBA career path, joint-degrees have an industry-focus or field-focus. For example, Stanford has joint degrees focusing on education and business, while Darden has MD/MBA programs for those who are studying to be trained doctors and who need business skills. Graduates tend to be younger (24 to 30) and prefer full-time studies, as this degree is meant to gain access into a certain field by combining studies and credentials. data on top-10 programs is abundant (hovering around $150,000 on average), but it’s a little more diffuse with other programs. Statistics for schools with lower rankings are less reliable but show an average of $50,000. That does not mean necessarily that the MBA world is bifurcated, but rather that there is a fairly broad spectrum. Also, it does mean that location matters and you should do your research on programs first based on fit, and then do digging into the benefits.[/list] [*]Network – For many, this is the indisputable top benefit of an MBA course, which should definitely be weighed when considering online programs. You have access to an alumni network regardless (formally, through the university, and informally through shared bonds that are more likely to get you to connect with alumni in your chosen field).[/list] [*]Higher employment rate – This is very program-specific, but generally, there is a higher chance of being employed consistently with an MBA. What is less clear, however, is the data behind their figures, which we’ll discuss a bit later here.[/list] [*]Access to higher-paying roles – The highest-paying roles after graduation tend to be (in descending order of average pay): consulting, financial services, and tech. What is also interesting is that those who get an MBA have the biggest salary increases in these industries (again, in order): consulting, food/beverage, investment management, and private equity, averaging $40,000 higher salary per year after graduation.[/list] On their own websites, MBA programs also highlight tangential benefits like increased confidence, better personal financial management, time-management skills, and broader worldview, but the data they used to gather such insights tends to focus on the gains in the careers and skills of those who ultimately decided to get an MBA. In other words, for those that decided it was worth it, it ended up being worth it. What is missing from their research are the trajectories of those who decided on an MBA alternative, but those data are inherently hard to come by – as we don’t have a reliable A/B test to understand what would have happened had they gone a different route. That means that MBA programs say MBAs are worth it, but you should definitely dig deeper to make sure they’re right for you. average debt accumulated from an MBA course is near $100,000, and so, most students are in fact paying a steep price for the programs. Given the hefty tuition costs, you’re probably wondering if the MBA is truly worth it. That’s a topic for another post, but let’s just focus on the financial aspect of it. There are various rules of thumb for deciding this, but one that is fairly reasonable is this: the bump in compensation you expect in your first three years as an MBA graduate should cover the out-the-door cost of the MBA. For example, if you paid 160,000 for a full-time MBA, but your post-MBA salary went from 90,000 to 110,000, you very well might want to give it a long, hard look to see if it was worth the cost (160,000 – 20,000×3 > 0) – as you have a deficit of 100,000 and likely a high-interest student loan capping your appetite for career mobility in the meantime. Conversely, if your post-MBA salary was up from 90,000 to 150,000 with a 160,000 price tag, now you’re looking at a much stronger business case (160,000 – 60,000×3 < 0), as that salary is now covering more 20,000 more than the cost of the program itself. Rough math? Yes. Hard to calculate future salary? Of course! The key point to take away here is to think of the MBA as any savvy business person would: what is the probable ROI (return on investment) and what is the opportunity cost? In other words, ask yourself: will it be worth its cost, and what else could I be doing at the same time? You’ll also be spending at least a year on the degree itself and likely 100+ hours on the application itself, so time is also a consideration. and in 2020, which is when many professionals decide that they’d like to boost their credentials and skills during a time with more uncertainty. Acceptance rates for universities have gone down recently due to an influx of applicants, hovering around 5% for most top-10 programs, for example. short-list of schools, the easiest way to apply is to fill out the application online on the specific program’s website. Luckily, it appears that, while the details can change, the portal in which you’ll put your information is very similar across most colleges. In addition to your undergraduate degree and transcripts from your degrees (likely going back to high school), here are additional admissions requirements and their considerations: Two letters of reference: Please check the university itself for the format, but luckily this tends to be uniform: (1) describe your relationship to the candidate, and (2) how do they compare to their peers. You can probably tell that this has a distinct bias for managers. It may feel awkward to ask your current employer for a recommendation, so clients, former managers, and professors could also be options. You will then need to give the contact information for your recommenders, who will then be emailed a link to fill in a page with their letter and often to answer questions about your aptitude (on a score from 1-9, with 9 being the highest, for each indicator). GMAT/GRE score (or an Executive Assessment for EMBAS): Check the requirements for your program, as some schools will even accept “expired” GMAT scores (older than 5 years). TOEFL or IELTS score: If your undergrad was not taught in English, it’s likely that you’ll be required to provide a TOEFL or IELTS score. This is program-specific, and some have loosened their requirement to look at other representations of English ability. Admissions essays: The typical essays are “Why ____ program” and “Tell us about you,” but the recent trend has been for universities has been to ask more unique questions (see Duke’s “25 random things about yourself” essay, for example). There is also an “essay” asking for any additional information, which is an opportunity to talk about mitigating factors and other considerations but is not typically written in an essay-like way as the others. Most programs expect a simple bullet-point list for the “Anything else” essay. An application fee: Fees can range from $50 to $300 but the idea is that each application is given consideration and so this covers the university’s overhead. Be sure to look up the university’s “fee waiver” for which many program applicants can qualify. And the last thing you’ll need? Patience. For larger programs, it can take two or more months to hear back about interviews, but luckily their timelines are transparently communicated on their websites. It’s well worth it to first learn about programs, and then to mark the major dates in your calendar. need more time to increase your GMAT score. For the overwhelming majority of programs that begin in the Fall, your rough timeline is: Round 1 Deadlines: June to September of the preceding year (for example, a 2022 to 2023 program will close applications in Summer 2021). Start preparing your application in February. Round 2 Deadlines: December to February before the program (for example, a 2022 to 2023 program will close applications in the preceding Winter). Start preparing your application by September. Round 3 Deadlines: March to May of the same year (for example, a 2022 to 2023 program will close applications in Summer 2022). Start preparing your application in December. While we’re on the subject, you might be wondering in which round you should apply. That’s a tough question, but overall the rule is “the earlier, the better,” as Round 2 tends to have more applicants than Round 1 and more in Round 3 than 2. The tough situation in which many applicants find themselves is weighing between Round 3 of this year or Round 1 of next year. For that, we don’t have an easy answer, but the question you should ask yourself is: will my application be substantially better in three months? What You Need to Know about MBAs: A Summary An MBA can be valuable for your career, but it will likely come with a considerable price tag and 1-2 years of study (on top of around 3 months of preparation), so it’s well worth doing research and some serious introspection with the question: is this right for me? Also keep in mind that not all MBA programs are made the same, as there are degrees that may very well be more tailored to your career interests, or perhaps, frankly, none at all! If you’ve made it this far, congratulate yourself for doing research into what is right for you, and we wish you luck on whatever next steps you take. Let us know in the comments, are you planning on getting an MBA? The post Everything You Need to Know about Getting an MBA appeared first on Magoosh Blog — GMAT® Exam. |
08 Jan 2021, 14:00
| FROM Magoosh Blog: How to Solve GMAT Motion Problems |
|
Word Problems make up a majority of the quantitative section of the GMAT (almost 60 percent). Of the word problems they’ll face, students tend to need the most help with GMAT motion problems. This type of problem centers around the “dust” formula, which is short for Distance equals Speed multiplied by Time, or \(text{D}timestext{S}=text{T}\). But there are many varieties of motion problem, and we will discuss techniques for each of them. At the end of this article, you’ll also find motion word problems with solutions for you to test your knowledge! The Distance Equation[/*] [*]Multi-Segment Motion Problems[/*] [*]Average Speed[/*] [*]Multiple Traveler Questions[/*] [*]Shrinking and Expanding Gaps[/*] [*]Data Sufficiency[/*] [*]GMAT Motion Problems Review: Practice Problems[/*] [/list] Distance equals Speed multiplied by Time, or \(text{D}timestext{S}=text{T}\). If you learn this basic equation well, you’ll be able to dust your math troubles away! (Insert rimshot.)  We can rearrange this formula to determine that Speed is equal to Distance divided by Time.  And Time is equal to Distance divided by Speed.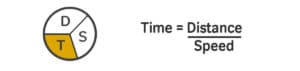 
Let’s demonstrate this. Walking at a constant rate of 160 meters per hour, Monroe can cross a bridge in 2 hours. What is the length of the bridge? Here, the length of the bridge is the distance Monroe must cross. Using Distance equals Speed multiplied by Time, we get: \((160;text{meters per hour})times(2;text{hours})=320;text{meters}\) Seems simple enough so far, right? Let’s check out a few more GMAT motion problems. Speed is equal to Distance divided by Time. Let’s take that a step further and talk about average speed. Average speed is defined as total distance traveled divided by the total time period spent traveling. This means that if you have a trip with multiple segments, you’ll want to take the sum of the distances of each segment and divide that by the sum of the times of each segment. Average speed captures the constant speed needed to travel the total distance in the total time. Let’s demonstrate this. Koki drove 16 miles in 10 minutes, and then drove an additional 6 miles in 5 minutes. What is Koki’s average speed for the entire trip in miles per hour? Click here for the answer and explanation Well, average speed is the total distance divided by the total time. \(text{D}_text{Total}=16;text{miles}+6;text{miles}=22;text{miles}\) \(text{T}_text{Total}=10;text{minutes}+5;text{minutes}=15;text{minutes}\) \(text{S}_text{Average}=frac{text{D}_text{Total}}{text{T}_text{Total}}\) \(text{S}_text{Average}=frac{22;text{miles}}{15;text{minutes}}timesfrac{60;text{minutes}}{1;text{hour}}=88;text{miles per hour}\) That’s straightforward enough, but what if we are not given any distances or times? It is possible to solve an average speed problem, even if all you are given are the different speeds in each segment of the trip. You might then think that average speed would just be the average of all of the speeds, but that is not correct. Let’s say that Nathaniel drove from Gwenville to Samton at an average speed of 24 miles per hour. He then drove the same route on the return trip back from Samton to Gwenville at an average speed of 36 miles per hour. If you were asked to find Nathaniel’s average speed, it would not just be 30 miles per hour (the average of 24 and 36). Click here to work through this problem To see this, let’s go back to our MVP dust formula. Since there are two legs of the trip, we will have two equations. D1, S1, T1; D2, S2, T2. Because Nathaniel’s trip is a round trip, we can assume that D1and D2 are the same, so we will set both of them equal to D. \(text{D}_1=text{D}\text{S}_1=24;text{miles per hour}\text{T}_1=frac{D}{24;text{miles per hour}}\) \(text{D}_2=text{D}\text{S}_2=36;text{miles per hour}\text{T}_2=frac{D}{36;text{miles per hour}}\) \(text{D}_text{Total}=text{2D}\) \(text{T}_text{Total}=frac{D}{24;text{miles per hour}}+frac{D}{36;text{miles per hour}}\) \(text{S}_text{Average}=frac{text{D}_text{Total}}{text{T}_text{Total}}\) \(text{S}_text{Average}=frac{text{2D}}{frac{D}{24;text{miles per hour}}+frac{D}{36;text{miles per hour}}}\) We can factor a D out of this fraction. \(text{S}_text{Average}=frac{2}{frac{1}{24}+frac{1}{36}};text{miles per hour}\) We can find a common denominator between 24 and 36. \(text{S}_text{Average}=frac{2}{frac{3}{72}+frac{2}{72}};text{miles per hour}\) \(text{S}_text{Average}=frac{2}{frac{5}{72}};text{miles per hour}=frac{2}{1}timesfrac{72}{5}=frac{144}{5};text{miles per hour}=28.8;text{miles per hour}\) In summary, whenever you want to find the average speed of a round trip, and you are given the two segment speeds, you can put it in the form \(text{S}_text{Average}=frac{text{2}}{frac{1}{text{S}_1}+frac{1}{text{S}_2}}\). You can also use this formula to find one of the segment speeds, given the other segment speed and the average speed. diagram. Let’s say that a car and truck are moving in the same direction on the same highway. The truck is moving at 50 miles an hour, and the car is traveling at a constant speed. At 3 pm, the car is 30 miles behind the truck and at 4:30 pm, the car overtakes and passes the truck. What is the speed of the car? Click here for the answer and explanation The car and truck are moving in the same direction, and the car is gaining on the truck. This means that the gap between the vehicles is shrinking and that the gap rate is the difference of the two vehicles’ respective speeds. \(text{S}_text{G}=text{S}_text{C}-text{S}_text{T}\) The distance of the gap is initially 30 miles. \(text{D}=30;text{miles}\) The time frame we are given for the closing of the gap is from 3 pm to 4:30 pm. \(text{T}=1.5;text{hours}=frac{3}{2};text{hours}\) \(text{S}_text{G}=frac{text{D}}{text{T}}\) \(text{S}_text{G}=frac{30;text{miles}}{frac{3}{2};text{hours}}=30timesfrac{2}{3}=20;text{miles per hour}\) \(20;text{miles per hour}=text{S}_text{C}-50;text{miles per hour}\) \(20;text{miles per hour}+50;text{miles per hour}=text{S}_text{C}=70;text{miles per hour}\) data sufficiency question from Magoosh, then review the video explanation.[/list] Let us know how you did on these practice questions in the comments below. If you’re looking for more GMAT motion problems, try out one of Magoosh’s GMAT plans, which comes with practice tests, video lessons, and study schedules. Good luck! The post How to Solve GMAT Motion Problems appeared first on Magoosh Blog — GMAT® Exam. |
08 Jan 2021, 14:00
| FROM Magoosh Blog: Everything You Need to Know about Getting an MBA |
|
An MBA, or a “Masters of Business Administration,” is a postgraduate degree achieved after an MBA candidate successfully goes through a business-focused program, usually lasting 1 to 2 years, and can be full-time or part-time. MBA programs are intended to better prepare you for business management skills and to make graduates more competitive in applying for leadership roles, or to crack into popular and high-paying industries, like tech, high-finance, and consulting. Check out our answers to frequently asked questions about the MBA below! What Is an MBA? [*]What Are the Benefits of an MBA?[*]What Do MBAs Cost?[*]How Hard Is an MBA?[*]Who Is an Ideal MBA Candidate?[*]How Do I Apply for MBA Programs?[*]When Should I Start Applying for an MBA?[/list] full-time and part-time MBA as both went through the same academic rigors. Online MBA Programs This is the broadest category here, as “online MBAs” could very well be EMBAs, full-time or part-time. Generally, the feature is in the name: it’s online, rather than in-person, but there are some hybrids. Scholarships, as noted above, are more plentiful for full-time in-person programs. Your mileage here will vary depending on the university, as many programs have deep wells of experience in facilitating connections and learning online, but others are a little newer to the scene and adapting to the increasing trend to move online.
Joint Degree Programs Best for those who have a more defined post-MBA career path, joint-degrees have an industry-focus or field-focus. For example, Stanford has joint degrees focusing on education and business, while Darden has MD/MBA programs for those who are studying to be trained doctors and who need business skills. Graduates tend to be younger (24 to 30) and prefer full-time studies, as this degree is meant to gain access into a certain field by combining studies and credentials. data on top-10 programs is abundant (hovering around $150,000 on average), but it’s a little more diffuse with other programs. Statistics for schools with lower rankings are less reliable but show an average of $50,000. That does not mean necessarily that the MBA world is bifurcated, but rather that there is a fairly broad spectrum. Also, it does mean that location matters and you should do your research on programs first based on fit, and then do digging into the benefits.[/list] [*]Network – For many, this is the indisputable top benefit of an MBA course, which should definitely be weighed when considering online programs. You have access to an alumni network regardless (formally, through the university, and informally through shared bonds that are more likely to get you to connect with alumni in your chosen field).[/list] [*]Higher employment rate – This is very program-specific, but generally, there is a higher chance of being employed consistently with an MBA. What is less clear, however, is the data behind their figures, which we’ll discuss a bit later here.[/list] [*]Access to higher-paying roles – The highest-paying roles after graduation tend to be (in descending order of average pay): consulting, financial services, and tech. What is also interesting is that those who get an MBA have the biggest salary increases in these industries (again, in order): consulting, food/beverage, investment management, and private equity, averaging $40,000 higher salary per year after graduation.[/list] On their own websites, MBA programs also highlight tangential benefits like increased confidence, better personal financial management, time-management skills, and broader worldview, but the data they used to gather such insights tends to focus on the gains in the careers and skills of those who ultimately decided to get an MBA. In other words, for those that decided it was worth it, it ended up being worth it. What is missing from their research are the trajectories of those who decided on an MBA alternative, but those data are inherently hard to come by – as we don’t have a reliable A/B test to understand what would have happened had they gone a different route. That means that MBA programs say MBAs are worth it, but you should definitely dig deeper to make sure they’re right for you. average debt accumulated from an MBA course is near $100,000, and so, most students are in fact paying a steep price for the programs. Given the hefty tuition costs, you’re probably wondering if the MBA is truly worth it. That’s a topic for another post, but let’s just focus on the financial aspect of it. There are various rules of thumb for deciding this, but one that is fairly reasonable is this: the bump in compensation you expect in your first three years as an MBA graduate should cover the out-the-door cost of the MBA. For example, if you paid 160,000 for a full-time MBA, but your post-MBA salary went from 90,000 to 110,000, you very well might want to give it a long, hard look to see if it was worth the cost (160,000 – 20,000×3 > 0) – as you have a deficit of 100,000 and likely a high-interest student loan capping your appetite for career mobility in the meantime. Conversely, if your post-MBA salary was up from 90,000 to 150,000 with a 160,000 price tag, now you’re looking at a much stronger business case (160,000 – 60,000×3 < 0), as that salary is now covering more 20,000 more than the cost of the program itself. Rough math? Yes. Hard to calculate future salary? Of course! The key point to take away here is to think of the MBA as any savvy business person would: what is the probable ROI (return on investment) and what is the opportunity cost? In other words, ask yourself: will it be worth its cost, and what else could I be doing at the same time? You’ll also be spending at least a year on the degree itself and likely 100+ hours on the application itself, so time is also a consideration. and in 2020, which is when many professionals decide that they’d like to boost their credentials and skills during a time with more uncertainty. Acceptance rates for universities have gone down recently due to an influx of applicants, hovering around 5% for most top-10 programs, for example. short-list of schools, the easiest way to apply is to fill out the application online on the specific program’s website. Luckily, it appears that, while the details can change, the portal in which you’ll put your information is very similar across most colleges. In addition to your undergraduate degree and transcripts from your degrees (likely going back to high school), here are additional admissions requirements and their considerations: Two letters of reference: Please check the university itself for the format, but luckily this tends to be uniform: (1) describe your relationship to the candidate, and (2) how do they compare to their peers. You can probably tell that this has a distinct bias for managers. It may feel awkward to ask your current employer for a recommendation, so clients, former managers, and professors could also be options. You will then need to give the contact information for your recommenders, who will then be emailed a link to fill in a page with their letter and often to answer questions about your aptitude (on a score from 1-9, with 9 being the highest, for each indicator). GMAT/GRE score (or an Executive Assessment for EMBAS): Check the requirements for your program, as some schools will even accept “expired” GMAT scores (older than 5 years). TOEFL or IELTS score: If your undergrad was not taught in English, it’s likely that you’ll be required to provide a TOEFL or IELTS score. This is program-specific, and some have loosened their requirement to look at other representations of English ability. Admissions essays: The typical essays are “Why ____ program” and “Tell us about you,” but the recent trend has been for universities has been to ask more unique questions (see Duke’s “25 random things about yourself” essay, for example). There is also an “essay” asking for any additional information, which is an opportunity to talk about mitigating factors and other considerations but is not typically written in an essay-like way as the others. Most programs expect a simple bullet-point list for the “Anything else” essay. An application fee: Fees can range from $50 to $300 but the idea is that each application is given consideration and so this covers the university’s overhead. Be sure to look up the university’s “fee waiver” for which many program applicants can qualify. And the last thing you’ll need? Patience. For larger programs, it can take two or more months to hear back about interviews, but luckily their timelines are transparently communicated on their websites. It’s well worth it to first learn about programs, and then to mark the major dates in your calendar. need more time to increase your GMAT score. For the overwhelming majority of programs that begin in the Fall, your rough timeline is: Round 1 Deadlines: June to September of the preceding year (for example, a 2022 to 2023 program will close applications in Summer 2021). Start preparing your application in February. Round 2 Deadlines: December to February before the program (for example, a 2022 to 2023 program will close applications in the preceding Winter). Start preparing your application by September. Round 3 Deadlines: March to May of the same year (for example, a 2022 to 2023 program will close applications in Summer 2022). Start preparing your application in December. While we’re on the subject, you might be wondering in which round you should apply. That’s a tough question, but overall the rule is “the earlier, the better,” as Round 2 tends to have more applicants than Round 1 and more in Round 3 than 2. The tough situation in which many applicants find themselves is weighing between Round 3 of this year or Round 1 of next year. For that, we don’t have an easy answer, but the question you should ask yourself is: will my application be substantially better in three months? What You Need to Know about MBAs: A Summary An MBA can be valuable for your career, but it will likely come with a considerable price tag and 1-2 years of study (on top of around 3 months of preparation), so it’s well worth doing research and some serious introspection with the question: is this right for me? Also keep in mind that not all MBA programs are made the same, as there are degrees that may very well be more tailored to your career interests, or perhaps, frankly, none at all! If you’ve made it this far, congratulate yourself for doing research into what is right for you, and we wish you luck on whatever next steps you take. Let us know in the comments, are you planning on getting an MBA? The post Everything You Need to Know about Getting an MBA appeared first on Magoosh Blog — GMAT® Exam. |
25 Jan 2021, 15:01
| FROM Magoosh Blog: Is an MBA Worth It? |
 Is an MBA worth it? Right now, most traditional MBAs aren’t. But some MBAs still are, depending on your situation. With that in mind, there are a lot of factors to consider before you completely write off doing a Master of Business Administration. MBAs are traditionally positioned as degrees that better prepare you for business management skills and that make graduates more competitive in applying for leadership roles, or to crack into popular and high-paying industries, like tech, high-finance, and consulting. However, there’s a recent declining interest in MBAs, even as applicant numbers are rising with economic stress. The main concern is that they aren’t able to keep pace with technological innovations that are changing the way businesses run. Beyond that, costs for traditional programs can be high—we’re talking hundreds of thousands of dollars. So, with all that in mind, the real question we should be asking is…which MBA programs are worth it? Which MBA Programs Are Worth it? Before you can know whether an MBA is worth it, you need to ask: what does an MBA get you? As we detail extensively in our general post about MBAs, here are the commonly cited benefits:
Here’s the rundown on the pros and cons of different MBA programs right now, as well as who they might be worth it for. The Value of a Full-Time MBA A full-time MBA generally is crafted for those with 2+ years of post-bachelor’s work experience. These are the traditional MBAs that most people picture, involving coursework guided by a core curriculum, team capstones, and an MBA thesis supported by faculty. Full-time MBA programs are typically two years, but sometimes the two-year curriculum is squeezed into one-year programs, making for a much more intense experience. In 2021, a full-time MBA may not have the same weight as it did even two years ago. We’re not living in normal times. You won’t be able to count on a lot of the benefits of a traditional full-time MBA program for your career, given the economic uncertainty that’s accompanying the pandemic and the resulting rise in applicants. It’s hard to say what the hiring process will look like for professionals a year from now. Also, given that most traditional MBA programs aren’t meeting in-person due to the COVID-19 pandemic, the huge price tag that comes attached means that you’re getting a lot less value than you normally would. No in-person classes, far less networking, scarce internship opportunities… There are a few exceptions, of course. Two big factors to take into consideration are rankings and scholarships A top business school degree (think: Harvard, Wharton) will almost always be an asset, coming with huge opportunities and higher earning potential, even in a terrible job market. And if you can offset the price with scholarships, the math just might add up. That’s not snobbery—it’s based on data. And the data on top-10 programs is abundant (average MBA salaries hovering around $173,860 on average), but it’s a little more diffuse with other programs. When looking at all MBA programs, the average falls sharply to $106,757. And keep in mind that’s the average across all programs; it’s weighted by those higher salaries from top-10 graduates. The Value of a Joint-degree MBA Joint-degree programs typically combine the traditional MBA with a traditional program in another field, such as an MD or Master in Public Policy, to allow candidates to build expertise at the intersection of business and the other field in question. Joint-degrees typically last the same amount of time minus one year of the combined length of the programs. Because joint-degrees are more expensive than the traditional MBA alone, the cost-benefit analysis is arguably more critical, especially in these times. In general, joint-degree programs are best for those who have a more defined post-MBA career path. It may also be worth it if you can find a prestigious fellowship (ahem) or scholarship to offset the cost. The Value of a Part-Time MBA Although part-time MBAs lack many of the networking benefits of a full-time MBA and it’s hard to qualify for a grant or scholarship for these programs, they do provide access to some alumni networks and on paper (i.e. your CV), there is virtually no difference between a part-time and full-time MBA. A part-time MBA is worth it for those who need the degree itself for a particular purpose, such as getting a promotion in their current company, and can take on the financial burden without going into significant debt. The Value of Online MBA Programs Although there could be an argument for ALL MBA programs qualifying as online MBA programs these days, true online MBA programs are meant to be conducted in an online setting. Whether an online MBA is worth it depends entirely on the program itself in terms of the education and opportunities it offers you. This option is most valuable to students who need flexibility and are assured of their program’s quality and offerings. If you’re considering getting an online MBA, make sure to connect with alumni, as rankings can only tell you so much in the new landscape. Is an MBA Worth It? A Summary Any MBA program is a big investment. Here’s when they’re worth it:
What is missing from their research are the trajectories of those who decided on an MBA alternative, but those data are inherently hard to come by – as we don’t have a reliable A/B test to understand what would have happened had they gone a different route. That means that MBA programs say MBAs are worth it, but you should definitely dig deeper to make sure they’re right for you. The post Is an MBA Worth It? appeared first on Magoosh Blog — GMAT® Exam. |
25 Jan 2021, 19:01
| FROM Magoosh Blog: GMAT Fee Waiver: How to Apply |
 The GMAT can be a pricey test. In the United States, it costs $275 for the exam alone (though it’s less in other locations, like the $250 India GMAT fee). If this isn’t in your budget, you do have options—primarily getting a GMAT fee waiver. We’ll take a look at what GMAT fee waivers are and what they cover, how to get one, and how to use them. What are GMAT fee waivers?[/*] [*]How do I get a fee waiver for GMAT?[/*] [*]Which business schools accept GMAT fee waivers?[/*] [*]How do I use my fee waiver?[/*] [/list] GMAT exam cost. In other words, they let you take the exam for a reduced price or even for free. Because students apply to their schools, not the GMAC (the Graduate Management Admission Council, AKA the the test-maker) for these waivers, it’s your school that ultimately decides how much of the fee gets waived. As you look for ways to reduce GMAT costs, keep in mind that a GMAT fee waiver is different from other types of waivers!
DANTES (Defense Activity for Non-Traditional Education Support) reimbursement. This only includes the test fee itself. It won’t pay off late fees, rescheduling fees, or other associated costs. You’ll also have to pay the money up-front yourself and then apply for DANTES reimbursement after you take the test. You need both your receipt and your results to get paid back. Make sure to apply within 90 days of your test date by submitting an online request. For military veterans, the GI Bill will reimburse you for the cost of one test. Note that GRE waivers are also available, which some MBA programs will accept. GMAT Fee Waivers and Covid-19 While lots of business schools have adjusted to the COVID-19 pandemic, one part remains the same: the fee waiver program. This hasn’t been expanded or changed as of right now. However, the good news is that 38% of MBA programs responding to the GMAC’s survey have reduced or removed application fees, so you may still end up saving money during the application process. University of Arkansas at Little Rock[*]Eastern Illinois University[*]University of North Dakota[*]University of Rhode Island[*]SUNY Polytechnic Institute[*]Cal State LA[/list] GMAT Fee Waiver: How to Apply appeared first on Magoosh Blog — GMAT® Exam. |
30 Jan 2021, 00:01
| FROM Magoosh Blog: GMAT Registration | How to Register for the GMAT |
 You’ve decided to take the next step in your career and go to business school. Congratulations! Now, down to brass tacks: GMAT registration. From ID to fees, here’s everything you need to know about how to register for the GMAT! How do I register for the GMAT?[/*] [*]How much is the GMAT registration fee?[/*] [*]How many days before should I register for the GMAT?[/*] [*]What happens after I register for the GMAT?[/*] [/list] GMAC’s “Create Your Account” page to get started. Once that’s done, you’ll have the ability to browse and pick your GMAT location and see your options for GMAT dates.[/*] [*]If you’re requesting GMAT accommodations, follow this process—you’ll need to get approval before registering. For any questions, email testingaccommodations@gmac.com or call customer service toll-free +1-800-717-GMAT.[/*] [/list] [/*] [*]Next, find a GMAT test center or prepare for the at-home online GMAT. (For GMAT registrations in early 2021, check here for the latest information). To find a GMAT location near you, use the GMAT’s official test center search page. And remember, the farther in advance you book your GMAT, the more options you’ll have for both GMAT locations and GMAT dates.[/*] [*]Once you are registered to take the GMAT and know your GMAT test center location, you’re ready to actually select your GMAT test date. Note that you have to pick a date and time to complete your GMAT test registration. Log in to your GMAT account and follow the on-screen instructions.[/*] [/list] GMAT Registration Checklist For GMAT exam registration, you’ll need to give the following info on the GMAT appointment scheduling form:
You’ll also have the option of entering your education history, your employment history, and your native language, but these aren’t mandatory parts of GMAT registration. How many times can I sign up for the exam? You can only be registered for one GMAT administration at a time. In other words, even if you’re planning on retaking the exam, you’ll need to schedule your second GMAT registration after you take the first test. Yes, that means you’ll need to pay the GMAT exam registration fees again, too. There’s also a limit to how many times you can take the GMAT in a single calendar year: 5 times. Once you’ve reached your GMAT registration attempt limit, you will have to wait for next year. Finally, keep in mind that you’ll need to have a 16-day gap between official GMAT exams. India, Africa, the Middle East, Asia Pacific and most of the world is $250 (USD), but that price can differ in the USA, Canada, and Europe—see our article “How Much Does the GMAT Cost?” for details. GMAT handbook from the Graduate Management Admission Council to get your bearings. If you haven’t already started studying, or if you need help organizing your schedule, Magoosh’s GMAT study plans can help get you where you need to be. Or dive right into a GMAT practice test to see how your current skills measure up and where you need to improve before your test day! The post GMAT Registration | How to Register for the GMAT appeared first on Magoosh Blog — GMAT® Exam. |
10 Feb 2021, 12:01
| FROM Magoosh Blog: How to Tackle Critical Reading Assumption Questions |
 Assumption questions ask you to find the unstated link between a question’s premise and its conclusion. Assumptions are crucial in understanding and refuting arguments, so they play a large role in two major Critical Reasoning question types. In this post, we’ll cover GMAT Critical Reasoning tips and practice questions to help you tackle assumption questions. GMAT Critical Reasoning Tips: How to Tackle Assumption Questions Luckily, arguments on GMAT Critical Reasoning questions are relatively formulaic, so let’s go over the basics first:
Make Your Assumption a General Statement This is a crucial point to remember: assumptions are most often general statements, not specific statements. When you identify the assumption, you can omit any specific people, places, or items mentioned. If my premise is “Fred has quality A,” and my conclusion is “Therefore, Fred has quality B,” Fred is a specific person that we can omit (sorry, Fred). The assumption would be something like “most/all folks who have quality A also have quality B.” Identify the Assumption Isolating an assumption is an important skill and one of our favorite GMAT Critical Reasoning tips. Let’s try it with this argument: Hawaii is a place with beautiful scenery. Therefore, people there must have trouble concentrating for any length of time at all.
Now, consider an argument you’re more likely to see on the GMAT: Of all the companies in the steel industry in the last six months, only Amalgamated Ferric Industry (AFI) has tripled their advertising expenditures. No other steel company has increased advertising nearly that much. Therefore, in the coming months, we should see AFI gaining new customers at a rate that outpaces all its competitors.
Use the Negation Test to Verify the Assumption If you want to verify that your assumption is really the correct one, you can use the Negation Test—put simply, try negating the statement and seeing if the conclusion is still true. If you haven’t tried the Negation Test yet (another of our key GMAT Critical Reasoning tips!), then I would definitely recommend checking out our post and studying this powerful technique for isolating assumptions of arguments. Practice Questions and Explanations Prof. Hernandez’s monumental work The History of Central America covers everything about the region from the origin of the Mesoamerican period to the end of the Cold War. While the book has several informative maps and charts, many of the chapters spend less time describing facts and more time explaining Prof. Hernandez’s theories. Indeed, the last two chapters consist exclusively of his exposition of theory of the role of Central America in post WWII world politics. Therefore, properly speaking, this book is not a history book. 1. Which of the following is an assumption that supports drawing the conclusion above from the reasons given for that conclusion? (A) Some history books consist almost exclusively of catalogues of historical facts. (B) Different historians have different understanding of the relative importance between facts and theories within the study of history. (C) Historians should be more explicit than most are now about the theoretical framework with which they write. (D) History as a discipline is concerned only with historical facts, not with the theoretical explanations of those facts. (E) Most books that present a wealth of historical facts include maps and charts as well. Click here for the answer and video explanation! In the twentieth century, the visual arts have embarked on major experimentation, from cubism to expressionism. While tastes always vary, there are certainly some people who find beautiful objects of each of the art movements of the first half of the twentieth century. In the latter half of the twentieth century, though, most works are so abstract or shocking that neither the critic nor the general public uses the word “beautiful” to describe them: indeed, sometimes late twentieth-century artists have, as one of their expressed goals, the creation of a work that no one could find beautiful. Whatever these artists are creating may be intellectually engaging at some level, but it is no longer art. 2. Which of the following is an assumption that supports drawing the conclusion above from the reasons given for that conclusion? (A) Art critics generally have a different appraisal of a work of art than does the general public. (B) The meaning of any work of art is defined entirely by the ideas of the artist who created it. (C) Beauty is a defining quality of art. (D) All art movements of the latter half of the twentieth century are responses to the movements of the first half of the century. (E) It is not possible for any work to be simultaneously beautiful and intellectually engaging. Click here for the answer and video explanation! Most people can gain vitamin C from fruits such as oranges and cantaloupes. People with Laestrygonian Disease have weakened digestive systems that cannot digest fruit or vitamin supplements. The easiest foods for these people to digest are grains such as rice and barley. Regular intake of vitamin C would be extremely beneficial to those who suffer from Laestrygonian Disease, so scientists have figured out a way to create “fortified rice” by infusing rice with high doses of vitamin C. This fortified rice will provide great benefit to those with Laestrygonian Disease. 3. Which one of the following is an assumption on which the conclusion depends? (A) Eventually, this fortified rice will be the optimal way for most people to have a regular intake of vitamin C. (B) The problems that folks with Laestrygonian Disease have digesting fruit are different from their problems digesting vitamin supplements. (C) People with Laestrygonian Disease will not be unable to assimilate the form of vitamin C that is present in the fortified rice. (D) Only people whose diets consist largely of grains would be able to derive benefit from the vitamin C in the fortified rice. (E) Vitamin C is the only nutrient which can be infused into rice in such high quantities without compromising the nutritional integrity of the vitamin. Click here for the answer and text explanation If folks with Laestrygonian Disease cannot assimilate the Vitamin C in the rice, then it won’t help them, and eating the fortified rice will not provide them any particular benefit. If we negate this option, it shatters the argument. This is a true assumption. (A) This may be true, although I am skeptical that any human-made improved food would be better than the fruits designed by Nature! Regardless, whether this is true or not does not have any bearing on how helpful the fortified rice will be for the folks with Laestrygonian Disease. This option is incorrect. (B) This is intriguing. Let’s negate this. Suppose it were the exact same problem, say, the exact same missing enzyme, that made it impossible to digest both fruit and vitamin supplements. Then what? Would that mean they also couldn’t digest the fortified rice, or get the vitamin C they need from it? We cannot say. It’s conceivable that the argument could still work, so negating this does not destroy the argument. This is not an assumption. (D) Let’s negate this. Suppose the fortified rice benefits everyone—even the no-carbs fanatic who hasn’t touched carbs in a decade: even when this person breaks his carb-fast and has the fortified rice, he has benefit from it. What then? Whether these other people benefit or not from the fortified rice has no bearing on whether it helps the folks with Laestrygonian Disease. This choice is incorrect. (E) Let’s negate this. Suppose we can infused dozens of other vitamins and minerals into the rice, all with high nutritional yield. That would only be good for the folks with Laestrygonian Disease—the more vitamins, the better! It certainly would not impact whether these folks derived any benefit from the vitamin C in the rice. This choice is incorrect. The answer is (C). Final Thoughts Assumption questions will require you to read closely, but with practice you can identify the missing link. For more GMAT Critical Reasoning tips, check out our introduction to the CR section. The post How to Tackle Critical Reading Assumption Questions appeared first on Magoosh Blog — GMAT® Exam. |
25 Mar 2021, 21:01
| FROM Magoosh Blog: The Best GMAT Prep Courses: 2021 Edition with Comparison Charts |
 Choosing the best GMAT prep course, like choosing a business school, is all about what works best for you as an individual. There is no objectively ‘best’ course that is right for everyone, but there are eight GMAT courses that should be on your radar in deciding which option suits your needs. One way to choose a course is to attend a free session or engage with some free material to see what suits you best. To make your decision, you’ll have to consider your learning style, and which course elements—from price to score guarantees—matter most to you. Don’t worry. We’ve done the hard work for you and have broken down the pros and cons of what we consider the eight best GMAT online prep courses. Magoosh $249 (get 10% off here!)$110 per hour50+ score improvement guarantee1,300+ practice questions and two practice tests. Subscribers get a 40% discount on GMAT  Official Practice Exams One-year access Princeton Review$799$167 an hour 620+ starting score required to be eligible for the guarantee of a 700+ score3,000+ practice problems and 10 practice tests Four-month access Target Test Prep$99 per month to $399 for 6 months access$300 per hourScore improvement guarantee only applies to your quantitative score3,000+ practice questionsOne-month to four-month access Manhattan Prep$549$225 per hourN/A1,100+ questions and six practice tests Six-month access Kaplan$599 - $799$2,499 for 10 hoursScore improvement guarantee5,000+ questions and nine practice testsSix-month access PrepScholar$2594 hours of tutoring from $799 60+ score guarantee Access to 1,000+ questions and 4 practice tests One-month to four-month access e-GMAT$349N/AN/A4,500+ questions and five practice testsSix-month access Veritas Prep$699$2,650 for 10 hours 50+ score improvement guarantee5,000+ questions and 12 practice tests One-year access  best GMAT books lists. Pros:
computer adaptive practice tests[/list] Review PrepScholar’s GMAT prep course is designed around personalization. Students take a diagnostic test upfront, and their proprietary algorithm works to create a custom study plan. You can also see which skills you have mastered and which you still need to work on on your student dashboard. Pros:
GMAT idioms flashcards app from Magoosh gives you all the most tested idioms specific to the GMAT, in an easy-to-learn flashcard format. Speaking of easy-to-learn flashcard formats, the Magoosh Math flashcards give you an overview of all the GMAT math rules. While math is very much about practice, these flashcards make the general rules that you’ll need for Data Sufficiency more explicit and easier to remember. If you are looking for a mental math workout before the test, look no further than the Math Tricks app and Calculator: The game app which allow you to practice the mental math tricks that can speed up your problem-solving in the GMAT. While these are not GMAT apps per se, they will help you to solve mental math problems more quickly and creatively. The Wiley Efficient Learning mobile app also needs a mention as a must-have GMAT app. It is essentially a more portable version of the Official Guide. It will give you access to the same Official Guide Questions in the book and online question bank, just on the go. What materials should I use in my GMAT prep? Show Answer You’ll want to get a copy of the GMAC Official guide so you can practice with real GMAT questions. But you’ll also need some guidance on how to answer the questions. For insights, tools, and strategies, you should get hold of some kind of GMAT prep books or courses. Don’t underestimate the usefulness of a GMAT study schedule. Learn how to build your own GMAT study schedule to keep yourself motivated and accountable. Remember the best GMAT prep materials are the ones that work best for you. Part of the emphasis on practice is to get a sense of what works for you. Everyone is slightly different in their approach so experiment while you are practicing to adapt generic strategies to your benefit. Whichever method of study you choose, try not to get too bogged down in the theory. Don’t learn the theory in isolation without considering how the GMAT tests different concepts. The GMAT is all about practice—and gaining as much insight into the test and the question types as you can from each question you practice. In your first phase of studying you might find it useful not to focus too heavily on timing. Rather, learn the concepts at your own pace. Once you have a good idea of how to answer questions you can introduce timing in the second phase. Lastly, you should have practiced a number of mock tests before you take the GMAT to get a feel of the test, build up stamina and see what checks and balances you can introduce to improve your score. These are our top picks for the best GMAT online prep courses! Like we mentioned earlier, the best GMAT prep course may vary greatly depending on your study style, strengths and weaknesses, and even your reason for taking the GMAT. Nevertheless, we hope this list can help you decide which prep course or study method works best for you. Good luck!  The post The Best GMAT Prep Courses: 2021 Edition with Comparison Charts appeared first on Magoosh Blog — GMAT® Exam. |
08 Apr 2021, 11:01
| FROM Magoosh Blog: How to Understand Your GMAT Percentiles |
 How can you turn test scores and section scores into GMAT score percentiles? And what about GMAT Quant score percentiles and Verbal score percentiles? Don’t worry—we’ve got all the info you need to know to understand your score. First off, your total GMAT score ranges from 200-800, and your section scores have their own score scales as well. But focusing on your GMAT percentiles can give you extra insight into your strengths and weaknesses on the test. The GMAT is all about competitive advantage. Your score is literally determined by how well you perform in relation to hundreds of thousands of test-takers over the past three years. In a nutshell, a ranking in the 75th percentile means that 25% of test-takers performed as well or better than you, and 75% did not. Knowing the percentiles lets you know if you’ve merely achieved an average GMAT score, or if you’ve shot through the roof with your scores. GMAC produces this information on GMAT percentile charts. For your convenience, we’ve broken these scores down below. This post has been updated to include GMAC’s most recently published GMAT score percentiles, which represent a sample of nearly 700,000 students who took the GMAT from 2017-2019. GMAT Score Percentiles Chart[/*] [*]GMAT Quant Percentiles[/*] [*]GMAT Verbal Percentiles[/*] [*]GMAT AWA Percentiles[/*] [*]GMAT IR Percentiles[/*] [*]How does GMAT calculate percentiles?
information on GMAT score calculations!) Click here for the GMAT Score Percentiles Chart PercentileScorePercentile (cont'd.)Score (cont'd.) 99%760-80030%520 98%75027%510 97%74025%500 96%73023%490 94%72021%480 91%71019%470 88%70017%460 85%69015%450 82%68014%440 80%67013%430 77%66012%420 73%65010%410 67%6409%400 65%6308%390 62%6208%380 58%6107%370 54%6006%360 51%5905%350 47%5805%340 44%5704%320-330 41%5603%300-310 38%5502%260-290 35%5401%220-250 31%5300%200-210  MBA.com are the best way to get an accurate idea of how you are performing before test day. The one-time thinking about the scoring algorithm, percentiles, and the difficulty level of questions is super unhelpful is during the test itself. It’s a waste of mental energy and effort, in part due to the experimental questions in the test, that doesn’t count towards your total score. as they did in 2017-2018), that means around:
retake the GMAT (and, unfortunately, pay the GMAT exam fee once more). Bear in mind that some schools will have minimum sectional scores for the Quant section as well. Others may insist on a ‘balanced score’ between the two sections. To understand the GMAT score you’ll need to obtain for a top school, the best thing to do is look at average GMAT scores for top programs. As you can see from running down this list, they all tend to be above 700–sometimes well above 700, as in the case of Columbia (an average of 732!). Put this in terms of percentiles using the chart above. A 700 on the GMAT is in the 88th percentile, while a 732 would be around the 96th percentile. From this information, we can draw the conclusion that top schools need top scores. Rankings don’t correspond precisely to score percentiles—but in this case, it’s pretty fair to say that if you’re applying to a top-10 school, a score in the top 10% of GMAT test-takers (i.e. placing you in the 90th percentile above) is definitely a helpful tool. How to Understand Your GMAT Percentiles appeared first on Magoosh Blog — GMAT® Exam. |
08 Apr 2021, 11:01
| FROM Magoosh Blog: GMAT Test Dates | 2021, 2022, 2023 and Beyond! |
|
[img]https://magoosh.com/gmat/files/2017/02/GMAT-Test-Dates.jpg[/img] With the COVID-19 still a concern in 2021, [url=https://www.mba.com/service/testing/appointment-search]in-person[/url] GMAT test dates are limited, but [url=https://www.mba.com/exams/gmat-online/gmat-online-experience/about-the-gmat-online]at-home[/url] options are available—and will be permanently available going forward. In this post, we’ve covered some more vital information about the GMAT test dates for 2021—read on to find out more! [url=https://magoosh.com/gmat#dates]GMAT Test Dates (2021, 2022, 2023)[/url][/*] [*][url=https://magoosh.com/gmat#testcenter]The 3 Steps to Scheduling Your GMAT Test Date[/url][/*] [*][url=https://magoosh.com/gmat#appdates]MBA application dates[/url] [list] [*][url=https://magoosh.com/gmat#round1]Round 1[/url][/*] [*][url=https://magoosh.com/gmat#round2]Round 2[/url][/*] [*][url=https://magoosh.com/gmat#round3]Round 3[/url][/*] [/list] [*][url=https://magoosh.com/gmat#register]When do I need to register for the GMAT?[/url][/*] [*][url=https://magoosh.com/gmat#plan]When should I plan on taking the GMAT?[/url] [/list] [url=https://magoosh.com/gmat/gmat-online/]online, at-home GMAT[/url] testing options. Meanwhile, the GMAC (test-maker) began to offer the remote GMAT in April 2020; it’s offered every day, with multiple time slots. However, popular days and times can still fill up—the remote proctor aspect of the testing means that there are still limits to how many test-takers can sign up for the exam at a given time. With all of these GMAT test dates to choose from, should you just throw a dart at a calendar? No! You’ll ned to be strategic about picking your test date, because you’ll need your score for whatever MBA application round you choose. We’ll talk more about this later i the post! [url=https://magoosh.com/gmat#contents][img]https://magoosh.com/gmat/files/2017/07/back-to-top-button-1-150x40.png[/img][/url] [url=https://accounts.gmac.com/Account/Register]GMAC’s “Create Your Account”[/url] page to get started. Once that’s done, you’ll have the ability to browse and see your options for GMAT dates (and locations, if applicable). Step 2a: Find a test center with available GMAT dates Once you’ve registered with GMAC and have the ability to look at GMAT exam dates, the next step is to find a GMAT test center. For in-person dates, look under “Future GMAT Test Center Exams” and click “Register Now” or “Register as a Test Taker with Disabilities.” Each of these buttons will take you to options for your location. Remember, the farther in advance you book your GMAT, the more options you’ll have for both GMAT locations and GMAT dates. Step 2b : Pick a date for the online GMAT Because the online GMAT is available every day, the key to picking a GMAT test date online is finding the day and time that work best for you. To find test dates for a remote GMAT, select “Register for the GMAT Online Exam” under “Future GMAT Online Exams” on your MBA.com “My Account” page. Click on dates to see available time options. Step 3: Schedule Your Exam Once you know which test format you want to take and are registered to take the GMAT, you’re ready to actually select your GMAT test date. Follow the on-screen instructions within your GMAT account. Of course, there’s a lot more to registering for the GMAT and choosing your test date than just accessing and navigating the official GMAT website. Timing is a crucial consideration too. Below, we’ll look at when to register, and how to select the GMAT test date that’s right for you. [url=https://magoosh.com/gmat#contents][img]https://magoosh.com/gmat/files/2017/07/back-to-top-button-1-150x40.png[/img][/url] [url=https://magoosh.com/blog/live-updates-effects-of-coronavirus-on-standardized-testing/]CANCELLED in many locations in 2020[/url], but [url=https://magoosh.com/gmat/online-interim-gmat-exam/]online, home-based GMAT testing[/url] is available now.StudyRetake GMATEssays, etc...Round 1 due [url=https://magoosh.com/gmat#contents][img]https://magoosh.com/gmat/files/2017/07/back-to-top-button-1-150x40.png[/img][/url] [url=https://magoosh.com/gmat/gmat-101/]GMAT examination[/url]. [url=https://magoosh.com/gmat#contents][img]https://magoosh.com/gmat/files/2017/07/back-to-top-button-1-150x40.png[/img][/url] [url=https://www.mba.com/us/the-gmat-exam/gmat-exam-scores/your-score-report/send-your-scores.aspx]GMAC says[/url] it can take up to 20 days for your test to be reported to schools. That could actually mean 21 days, depending on whether your test day scores get transmitted from the test center to GMAT central the same day you take the test or the next day. There’s also a small chance that for some reason there could be unexpected delays in the GMAC sending our scores. So, beyond GMAT exam dates, you should consider the dates of arrival for your GMAT exam report. To be safe, you’ll want to book your GMAT date at least 21 days prior to your application deadline, so that there is ample time for your scores to be processed and sent to your school. Giving yourself a few extra days beyond the 21 can’t hurt either. So really, there’s an extra month in there. That’s why I recommend taking your GMAT 7-8 months before your deadline instead of just 6-7. Adjust the recommended GMAT application timeline to your personal needs Of course, your mileage may vary, in terms of how much time you really need and when you should register for the GMAT. If you have more than 20 hours a week to study or have higher-than-average GMAT skills, you may need less time to prepare for your exam or a possible retake. Conversely, if you have fewer hours of spare time per week or lower baseline skills for the exam, you may need to reserve more prep time before you actually take the test. Also, while it isn’t as common, some students get all of the soul searching, university visits, reference letter gathering and so on out of the way before they tackle the GMAT. If this sounds like you, then your GMAT prep time and GMAT exam date will take a different position in your overall timetable for admissions. [url=https://magoosh.com/gmat#contents][img]https://magoosh.com/gmat/files/2017/07/back-to-top-button-1-150x40.png[/img][/url] The post [url=https://magoosh.com/gmat/gmat-test-dates/]GMAT Test Dates | 2021, 2022, 2023 and Beyond![/url] appeared first on [url=https://magoosh.com/gmat]Magoosh Blog — GMAT® Exam[/url]. |
|
|
||
close
