dave13
pushpitkc

Since the depth of water is 1 meter, the volume of water contained is 4*2*1 = 8 meter^3
The various faces on which the cuboid can be turned are 2*3(6) or 3*4(12) since the cuboid is
already on its third face which is 2*4(8). The smallest face towards which the tank is moved
has an area of 6 meter^2.
Therefore, the depth of water is meter in the cube can be measured as \(\frac{4}{3}\) meter
(Option C) I omitted this step / couldnt see it --->
Since the depth of water is 1 meter, the volume of water contained is 4*2*1 = 8 meter^3but i did calculate the are of large rectangle which is 8
and area of smallest rectangle which is 6
so al we have to do is to write ratio the areas of above mentioned rectangles ? if So
my question IS why you wrote 4/3 and not 3/4, how should i figure out this - to write 4/3 or 3/4 ?
i hope you can take time to reply to my post

thank you

Hi
dave13,
I think you are confused with the application of Area and Volume.
In the above problem, the quantity(volume ) of water is going to be constant. Hence we equate the volume.
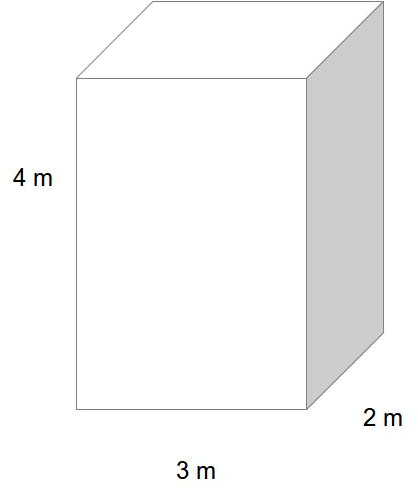
In the Original Diagram, we have the following dimensions:
Height = 3 cm but the height of the water is only 1 cm, hence consider height as 1 cm. Length = 2 cm and Width = 4 cm.
Volume = 2*4*1 = 8 \(cm^3\) ---- (1)
After rotation, we have the following diagram. Please note that the water level is not depicted in the diagram.
Attachment:
 rotated tank1.png [ 17.19 KiB | Viewed 6938 times ]
rotated tank1.png [ 17.19 KiB | Viewed 6938 times ]
After rotation we have the following dimensions:
Height = 4 cm but the height of water level is unknown, hence assume as \(h\) cm. Length = 3 cm, and Width = 2 cm.
The volume of water =\(h*3*2 = 6h\) --- (2)
By equating (1) and (2) we have \(h = \frac{4}{3}\)cm.
Hope this helps.
Please go through the following article:
https://study.com/academy/lesson/differ ... olume.htmlThank you.

 5%
(low)
5%
(low)
 15%
(01:55)
wrong
15%
(01:55)
wrong  based on 440
sessions
based on 440
sessions