Forum Home > GMAT > Quantitative > Problem Solving (PS)
Events & Promotions
| Last visit was: 26 Jul 2024, 16:28 |
It is currently 26 Jul 2024, 16:28 |

Customized
for You
Track
Your Progress
Practice
Pays
10:00 AM PDT
-11:00 AM PDT
11:00 AM IST
-01:00 PM IST
08:00 AM EDT
-11:59 PM EDT
10:00 AM PDT
-11:00 AM PDT
11:00 AM IST
-01:00 PM IST
05:55 AM PDT
-12:30 PM PDT
10:00 AM EDT
-11:59 PM PDT
Difficulty:


 25%
(medium)
25%
(medium)
Question Stats:
72% (01:02) correct 28%
(00:49)
wrong
28%
(00:49)
wrong  based on 2381
sessions
based on 2381
sessions
Please Note the following :-
1) Always post the question in relevant forum
i.e. Problem Solving Question is PS forum, Data Sufficiency question is DS forum, GMATClub test Question in GC Test forum.
2) Always post the question along with OA
3) Search the forum before posting a new question. This question is already discussed here.

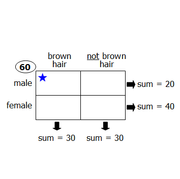
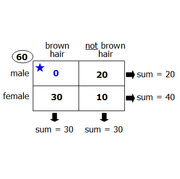
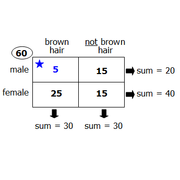













|
|
|
GMAT Club REWARDS
|