ADVANCED OVERLAPPING SETS PROBLEMS

Some 700+ GMAT quantitative questions will require you to know and understand the formulas for set theory, presenting three sets and asking various questions about them. There are two main formulas to solve questions involving three overlapping sets. Consider the diagram below:


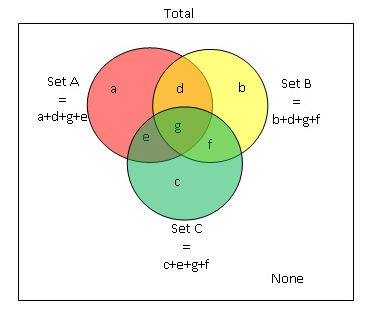FIRST FORMULA

\(Total = A + B + C - (sum \ of \ 2-group \ overlaps) + (all \ three) + Neither\).

Let's see how this formula is derived.

When we add three groups A, B, and C some sections are counted more than once. For instance: sections d, e, and f are counted twice and section g thrice. Hence we need to subtract sections d, e, and f ONCE (to count section g only once) and subtract section g TWICE (again to count section g only once).

In the formula above, \(sum \ of \ 2-group \ overlaps=AnB+AnC+BnC\), where AnB means intersection of A and B (sections d, and g), AnC means intersection of A and C (sections e, and g), and BnC means intersection of B and C (sections f, and g).

Now, when we subtract \(AnB\) (d, and g), \(AnC\) (e, and g), and \(BnC\) (f, and g) from \(A+B+C\), we are subtract sections d, e, and f ONCE BUT section g THREE TIMES (and we need to subtract section g only twice), therefor we should add only section g, which is intersection of A, B and C (AnBnC) again to get \(Total = A + B + C - (sum \ of \ 2-group \ overlaps) + (all \ three) + Neither\).

SECOND FORMULA

\(Total = A + B + C - (sum \ of \ EXACTLY \ 2-group \ overlaps) - 2*(all \ three) + Neither\).

Notice that EXACTLY (only) 2-group overlaps is not the same as 2-group overlaps:
Elements which are common only for A and B are in section d (so elements which are common ONLY for A and B refer to the elements which are in A and B but not in C);
Elements which are common only for A and C are in section e;
Elements which are common only for B and C are in section f.

Let's see how this formula is derived.

Again: when we add three groups A, B, and C some sections are counted more than once. For instance: sections d, e, and f are counted twice and section g thrice. Hence we need to subtract sections d, e, and f ONCE (to count sections d, e, and f only once) and subtract section g TWICE (again to count section g only once).

When we subtract \(sum \ of \ EXACTLY \ 2-group \ overlaps\) from A+B+C we subtract sections d, e, and f once (fine) and next we need to subtract ONLY section g (\(AnBnC\)) twice. That's it.

Now, how this concept can be represented in GMAT problem?

Example 1:
Workers are grouped by their areas of expertise, and are placed on at least one team. 20 are on the marketing team, 30 are on the Sales team, and 40 are on the Vision team. 5 workers are on both the Marketing and Sales teams, 6 workers are on both the Sales and Vision teams, 9 workers are on both the Marketing and Vision teams, and 4 workers are on all three teams. How many workers are there in total?

Translating:
"are placed on at least one team": members of none =0;
"20 are on the marketing team": M=20;
"30 are on the Sales team": S=30;
"40 are on the Vision team": V=40;
"5 workers are on both the Marketing and Sales teams": MnS=5, note here that some from these 5 can be the members of Vision team as well, MnS is sections d an g on the diagram (assuming Marketing = A, Sales = B and Vision = C);
"6 workers are on both the Sales and Vision teams": SnV=6 (the same as above sections f an g);
"9 workers are on both the Marketing and Vision teams": MnV=9.
"4 workers are on all three teams": MnSnV=4, section 4.

Question: Total=?

Applying first formula as we have intersections of two groups and not the number of only (exactly) 2 group members:

\(Total=M+S+V-(MnS+MnV+SnV)+MnSnV+Neither=20+30+40-(5+6+9)+4+0=74\).

Answer: 74. Discuss this question HERE.

Example 2:
Each of the 59 members in a high school class is required to sign up for a minimum of one and a maximum of three academic clubs. The three clubs to choose from are the poetry club, the history club, and the writing club. A total of 22 students sign up for the poetry club, 27 students for the history club, and 28 students for the writing club. If 6 students sign up for exactly two clubs, how many students sign up for all three clubs?

Translating:
"Each of the 59 members in a high school class is required to sign up for a minimum of one and a maximum of three academic clubs": Total=59, Neither=0 (as members are required to sign up for a minimum of one);
"22 students sign up for the poetry club": P=22;
"27 students for the history club": H=27;
"28 students for the writing club": W=28;
"6 students sign up for exactly two clubs": (sum of EXACTLY 2-group overlaps)=6, so the sum of sections d, e, and f is given to be 6, (among these 6 students there are no one who is a member of ALL 3 clubs)

Question:: "How many students sign up for all three clubs?" --> \(PnHnW=g=?\)

Apply second formula: \(Total=P+H+W -(sum \ of \ EXACTLY \ 2-group \ overlaps)-2*PnHnW + Neither\) --> \(59=22+27+28-6-2*x+0\) --> \(x=6\).

Answer: 6. Discuss this question HERE.

Example 3:
Of 20 Adults, 5 belong to A, 7 belong to B, and 9 belong to C. If 2 belong to all three organizations and 3 belong to exactly 2 organizations, how many belong to none of these organizations?

Translating:
"20 Adults": Total=20;
"5 belong to A, 7 belong to B, and 9 belong to C": A=5, B=7, and C=9;
"2 belong to all three organizations": AnBnC=g=2;
"3 belong to exactly 2 organizations": (sum of EXACTLY 2-group overlaps)=3, so the sum of sections d, e, and f is given to be 3, (among these 3 adults there are no one who is a member of ALL 3 clubs)

Question:: Neither=?

Apply second formula: \(Total=A+B+C-(sum \ of \ EXACTLY \ 2-group \ overlaps)-2*AnBnC + Neither\) --> \(20=5+7+9-3-2*2+Neither\) --> \(Neither=6\).

Answer: 6. Discuss this question HERE.

Example 4:
This semester, each of the 90 students in a certain class took at least one course from A, B, and C. If 60 students took A, 40 students took B, 20 students took C, and 5 students took all the three, how many students took exactly two courses?

Translating:
"90 students": Total=90;
"of the 90 students in a certain class took at least one course from A, B, and C": Neither=0;
"60 students took A, 40 students took B, 20 students took C": A=60, B=40, and C=20;
"5 students took all the three courses": AnBnC=g=5;

Question:: (sum of EXACTLY 2-group overlaps)=?

Apply second formula: \(Total=A+B+C-(sum \ of \ EXACTLY \ 2-group \ overlaps)-2*AnBnC + Neither\) --> \(90=60+40+20-x-2*5+0\) --> \(x=20\).

Answer: 20. Discuss this question HERE.

Example 5:
In the city of San Durango, 60 people own cats, dogs, or rabbits. If 30 people owned cats, 40 owned dogs, 10 owned rabbits, and 12 owned exactly two of the three types of pet, how many people owned all three?

Translating:
"60 people own cats, dogs, or rabbits": Total=60; and Neither=0;
"30 people owned cats, 40 owned dogs, 10 owned rabbits": A=30, B=40, and C=10;
"12 owned exactly two of the three types of pet": (sum of EXACTLY 2-group overlaps)=12;

Question:: AnBnC=g=?

Apply second formula: \(Total=A+B+C-(sum \ of \ EXACTLY \ 2-group \ overlaps)-2*AnBnC + Neither\) --> \(60=30+40+10-12-2*x+0\) --> \(x=4\).

Answer: 4. Discuss this question HERE.

Example 6:
When Professor Wang looked at the rosters for this term's classes, she saw that the roster for her economics class (E) had 26 names, the roster for her marketing class (M) had 28, and the roster for her statistics class (S) had 18. When she compared the rosters, she saw that E and M had 9 names in common, E and S had 7, and M and S had 10. She also saw that 4 names were on all 3 rosters. If the rosters for Professor Wang's 3 classes are combined with no student's name listed more than once, how many names will be on the combined roster?

Translating:
"E had 26 names, M had 28, and S had 18": E=26, M=28, and S=18;
"E and M had 9 names in common, E and S had 7, and M and S had 10": EnM=9, EnS=7, and MnS=10;
"4 names were on all 3 rosters": EnMnS=g=4;

Question:: Total=?

Apply first formula: \(Total = A + B + C - (sum \ of \ 2-group \ overlaps) + (all \ three) + Neither\) --> \(Total=26+28+18-(9+7+10)+4+0\) --> \(Total=50\).

Answer: 50. Discuss this question HERE.

Example 7:
There are 50 employees in the office of ABC Company. Of these, 22 have taken an accounting course, 15 have taken a course in finance and 14 have taken a marketing course. Nine of the employees have taken exactly two of the courses and 1 employee has taken all three of the courses. How many of the 50 employees have taken none of the courses?

Translating:
"There are 50 employees in the office of ABC Company": Total=50;
"22 have taken an accounting course, 15 have taken a course in finance and 14 have taken a marketing course"; A=22, B=15, and C=14;
"Nine of the employees have taken exactly two of the courses": (sum of EXACTLY 2-group overlaps)=9;
"1 employee has taken all three of the courses": AnBnC=g=1;

Question:: None=?

Apply second formula: \(Total=A+B+C-(sum \ of \ EXACTLY \ 2-group \ overlaps)-2*AnBnC + None\) --> \(50=22+15+14-9-2*1+None\) --> \(None=10\).

Answer: 10. Discuss this question HERE.

Example 8 (hard):
In a consumer survey, 85% of those surveyed liked at least one of three products: 1, 2, and 3. 50% of those asked liked product 1, 30% liked product 2, and 20% liked product 3. If 5% of the people in the survey liked all three of the products, what percentage of the survey participants liked more than one of the three products?

Translating:
"85% of those surveyed liked at least one of three products: 1, 2, and 3": Total=100%. Also, since 85% of those surveyed liked at least one of three products then 15% liked none of three products, thus None=15%;
"5% of the people in the survey liked all three of the products": AnBnC=g=5%;

Question:: what percentage of the survey participants liked more than one of the three products?

Apply second formula:
Total = {liked product 1} + {liked product 2} + {liked product 3} - {liked exactly two products} - 2*{liked exactly three product} + {liked none of three products}

\(100=50+30+20-x-2*5+15\) --> \(x=5%\), so 5% liked exactly two products. More than one product liked those who liked exactly two products, (5%) plus those who liked exactly three products (5%), so 5+5=10% liked more than one product.

Answer: 10%. Discuss this question HERE.

Example 9 (hard):
In a class of 50 students, 20 play Hockey, 15 play Cricket and 11 play Football. 7 play both Hockey and Cricket, 4 play Cricket and Football and 5 play Hockey and football. If 18 students do not play any of these given sports, how many students play exactly two of these sports?

Translating:
"In a class of 50 students...": Total=50;
"20 play Hockey, 15 play Cricket and 11 play Football": H=20, C=15, and F=11;
"7 play both Hockey and Cricket, 4 play Cricket and Football and 5 play Hockey and football": HnC=7, CnF=4, and HnF=5. Notice that "7 play both Hockey and Cricket" does not mean that out of those 7, some does not play Football too. The same for Cricket/Football and Hockey/Football;
"18 students do not play any of these given sports": Neither=18.

Question:: how many students play exactly two of these sports?

Apply first formula:

{Total}={Hockey}+{Cricket}+{Football}-{HC+CH+HF}+{All three}+{Neither}

50=20+15+11-(7+4+5)+{All three}+18 --> {All three}=2;

Those who play ONLY Hockey and Cricket are 7-2=5;
Those who play ONLY Cricket and Football are 4-2=2;
Those who play ONLY Hockey and Football are 5-2=3;

Hence, 5+2+3=10 students play exactly two of these sports.

Answer: 10. Discuss this question HERE.

Example 10 (hard DS question on three overlapping sets):
A student has decided to take GMAT and TOEFL examinations, for which he has allocated a certain number of days for preparation. On any given day, he does not prepare for both GMAT and TOEFL. How many days did he allocate for the preparation?

(1) He did not prepare for GMAT on 10 days and for TOEFL on 12 days.
(2) He prepared for either GMAT or TOEFL on 14 days

We have: {Total} = {GMAT } + {TOEFL} - {Both} + {Neither}. Since we are told that "on any given day, he does not prepare for both GMAT and TOEFL", then {Both} = 0, so {Total} = {GMAT } + {TOEFL} + {Neither}. We need to find {Total}

(1) He did not prepare for GMAT on 10 days and for TOEFL on 12 days --> {Total} - {GMAT } = 10 and {Total} - {TOEFL} =12. Not sufficient.
(2) He prepared for either GMAT or TOEFL on 14 days --> {GMAT } + {TOEFL} = 14. Not sufficient.

(1)+(2) We have three linear equations ({Total} - {GMAT } = 10, {Total} - {TOEFL} =12 and {GMAT } + {TOEFL} = 14) with three unknowns ({Total}, {GMAT }, and {TOEFL}), so we can solve for all of them. Sufficient.

Just to illustrate. Solving gives:
{Total} = 18 - he allocate total of 18 days for the preparation;
{GMAT } = 8 - he prepared for the GMAT on 8 days;
{TOEFL} = 6 - he prepared for the TOEFL on 6 days;
{Neither} = 4 - he prepared for neither of them on 4 days.

Answer: C. Discuss this question HERE.

Example 11 (disguised three overlapping sets problem):
Three people each took 5 tests. If the ranges of their scores in the 5 practice tests were 17, 28 and 35, what is the minimum possible range in scores of the three test-takers?
A. 17
B. 28
C. 35
D. 45
E. 80

Consider this problem to be an overlapping sets problem:
# of people in group A is 17;
# of people in group B is 28;
# of people in group C is 35;

What is the minimum # of total people possible in all 3 groups? Clearly if two smaller groups A and B are subsets of bigger group C (so if all people who are in A are also in C and all people who are in B are also in C), then total # of people in all 3 groups will be 35. Minimum # of total people cannot possibly be less than 35 since there are already 35 people in group C.

Answer: C.

P.S. Notice that max range for the original question is not limited when the max # of people in all 3 groups for revised question is 17+28+35 (in case there is 0 overlap between the 3 groups).

Answer: C. Discuss this question HERE.

____________________________________________________________________________________________________________
For more questions on overlapping sets check our Question Banks
Data Sufficiency Questions on Overlapping Sets
Problem Solving Questions on Overlapping Sets