Forum Home > GMAT > Quantitative > Problem Solving (PS)
Events & Promotions
| Last visit was: 06 Oct 2024, 03:03 |
It is currently 06 Oct 2024, 03:03 |

Customized
for You
Track
Your Progress
Practice
Pays
09:00 AM PDT
-12:00 PM PDT
01:30 PM IST
-11:30 PM IST
10:00 AM EDT
-11:00 AM EDT
10:00 AM EDT
-11:00 AM EDT
11:00 AM IST
-01:00 PM IST
Difficulty:


 5%
(low)
5%
(low)
Question Stats:
92% (01:31) correct 8%
(02:02)
wrong
8%
(02:02)
wrong  based on 2321
sessions
based on 2321
sessions
Solution
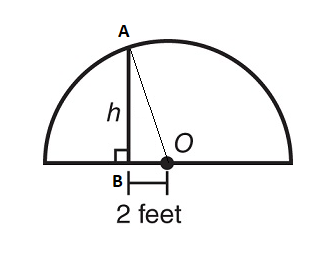

NEW question from GMAT® Official Guide 2019

NEW question from GMAT® Official Guide 2019



NEW question from GMAT® Official Guide 2019
Wanna make solving the Official Questions interesting???

|
|
|
Announcements
SUNDAY Quizzes! GRE Quiz @9:30am ET & GMAT Quiz @10:30am ET
Applying to Masters in Management? Join Top MiM Applicant Discussions
Tuck at Dartmouth
|