Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 12 Dec 2018, 03:22.
Last edited by EgmatQuantExpert on 17 Dec 2018, 04:14, edited 1 time in total.
Last edited by EgmatQuantExpert on 17 Dec 2018, 04:14, edited 1 time in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
Factorial is an interesting concept in number properties from which many application-oriented questions are asked in the GMAT. In this article, we will discuss one of the most frequently asked question types in factorials.
Objective of the article
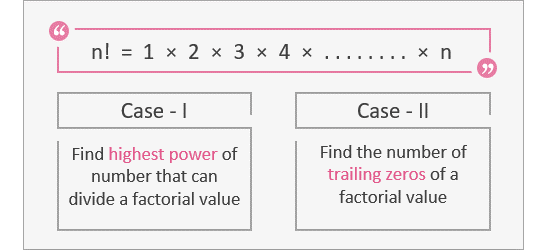
The primary objective of this article is to:
To explain the 2 scenarios, we have taken the help of 3 questions. The first 2 questions will be used to explain Case-1 and the third question will be used to explain Case-2.
Let’s start with the first scenario.
Case 1
The Context
Many times, we get questions on factorials where we need to find the highest power of a number present in the factorial. Sometimes, we also get questions where we need to find the number of trailing zeroes of a specific factorial value.
We will discuss both these cases one after the other and finally, relate them.
Question 1
The number n is obtained by multiplying the first 40 natural numbers. What is the value of the greatest integer p, for which \(5^p\) is a factor of n?
Understanding the Question
Let us read the question stem first and draw all the pertinent inferences from the given information.
In this question, we are given that n is a number which is obtained by multiplying the first 40 natural numbers.
So, re-framing the question, we can say that we need to find the greatest integer p, for which \(5^p\) is a factor of 40!
Approach & Solution
So now, let’s find the highest power of 5 in 40! by dividing 40 with 5 and its consecutive higher powers till it is possible to divide, and then add the quotients of all the divisions, to determine our answer.
At this point, some of you may wonder why are dividing 40 by \(5^1\) and \(5^2\) only? Let’s figure it out.
So, now let’s divide 40 by \(5^1\) and \(5^2\), to determine their individual instances.
\(5^1\) and \(5^2\) are the only two powers of 5 that can divide 40. Higher powers of 5 (for example, \(5^3\) = 125, or \(5^4\) = 625 etc.) are greater than 40, hence we will not consider them while dividing with powers of 5.
Therefore, the highest power of 5 in 40! = 8 + 1 = 9
In other words, we can also say that the greatest value of p, for which \(5^p\) is a factor of 40! Is 9.
So, the correct answer choice is option C.
Now, let’s solve one more similar question, to solidify our understanding.
Question 2
What is the highest power of 8, that can divide 88!?
Understanding the Question
This question is similar to the previous question that we solved a while ago. Hence, you may think that we can apply the same method here.
Let’s see what happens when we do that.
In this question, we are asked to find the highest power of 8 that can divide the number 88!
So, we must divide 88 by powers of 8, till division is possible, and then add the quotients to obtain the highest power of 8.
As \(8^3 = 512\) is greater than 88, we don’t need to consider that.
Hence, the highest power of 8 that can divide 88! = 11 + 1 = 12
So, the correct answer choice is option B, right?
Let’s analyse the question a bit more to understand the error.
Approach & Solution
When we divide 88! by 8 or powers of 8, we are only identifying and counting those numbers which are multiples of 8, such as 24, 32, 56 etc.
But, are these numbers the only ones by which we can get as a multiple of 8?
In such cases, what should we do? We need to first express the number in the prime factorized form.
Difference between Question 1 and Question 2
Well, we need to understand the fundamental difference between the two questions.
"Whenever we need to calculate the instances of any prime number in a factorial value, we can do that by directly dividing the factorial number by the prime number. But, if we have a composite number, then first we need to express the number in terms of its prime factors. We need to prime factorize because apart from the number and its powers, we can get the instances of the number from the combination of other numbers also". (For example, we can get 8 by 4 * 2 or 2 * 2 * 2, apart from 8 or powers of 8)
Once we get the prime factor(s) of the number, we need to find the instances of each of the prime factor(s), and then from them, the instances of the original number.
Now, let’s solve another variation of the similar concept, on the applications of factorials.
Case 2
The Context
Sometimes we get questions where we are given a factorial number, and we need to find the number of consecutive zeroes at the end of the value of the number, before the first non-zero digit from the right. This is another interesting application of the same concept of factorials that we discussed in the previous two questions. Let’s demonstrate that with an example.
Question 3
How many trailing zeroes would be found in 57! upon expansion?
Understanding the Question
In this question, we are given a number 57! and we are asked to find the number of trailing 0's at the end of the value of 57!
The value of 57! is effectively a number which we get by multiplying all the positive integers from 1 to 57. But how do get 0's at the end of a product of two or more numbers?
Now, this is a known application to us – in the previous question, we solved the same only. So, let’s follow the same approach.
Approach & Solution
As 10 is a composite number, first we need to express it in terms of its prime factorized form.
Now, we have 53 instances of 2's and 13 instances of 5's. We also know that, to form a 10, we need 1 instance of 2 and 1 instance of 5.
Hence, number of possible pairs of 2 and 5 = minimum (53, 13) = 13
Or, we can also say that the number of trailing 0's in 57! is 13.
Hence, the correct answer choice is option B.
Final Takeaways from the Article
Want to read more articles like this?
Now, if you liked this article, then I am sure that you want to read some more articles like this.
To read all our article go here: Must Read Articles and Practice Questions to score Q51 !!!!
You will also get a lot of practice questions to learn from.
Happy learning.
Variations in Factorial Manipulation
Factorial is an interesting concept in number properties from which many application-oriented questions are asked in the GMAT. In this article, we will discuss one of the most frequently asked question types in factorials.
Objective of the article
The primary objective of this article is to:
- • Demonstrate 2 different cases in which the concept of factorials can be applied to find the correct answer.
To explain the 2 scenarios, we have taken the help of 3 questions. The first 2 questions will be used to explain Case-1 and the third question will be used to explain Case-2.
Let’s start with the first scenario.
Case 1
The Context
Many times, we get questions on factorials where we need to find the highest power of a number present in the factorial. Sometimes, we also get questions where we need to find the number of trailing zeroes of a specific factorial value.
We will discuss both these cases one after the other and finally, relate them.
Question 1
The number n is obtained by multiplying the first 40 natural numbers. What is the value of the greatest integer p, for which \(5^p\) is a factor of n?
- A. 7
B. 8
C. 9
D. 10
E. 11
Understanding the Question
Let us read the question stem first and draw all the pertinent inferences from the given information.
In this question, we are given that n is a number which is obtained by multiplying the first 40 natural numbers.
- • Now, , when we multiply all the positive integers, starting from 1 to 40, both inclusive, we get 40!
• Hence, we can say n = 40!
So, re-framing the question, we can say that we need to find the greatest integer p, for which \(5^p\) is a factor of 40!
- • Doesn’t that also mean p is the highest power of 5 in the number 40!?
- o Yes, this is also another interpretation of the same statement.
Approach & Solution
So now, let’s find the highest power of 5 in 40! by dividing 40 with 5 and its consecutive higher powers till it is possible to divide, and then add the quotients of all the divisions, to determine our answer.
At this point, some of you may wonder why are dividing 40 by \(5^1\) and \(5^2\) only? Let’s figure it out.
- • In the number 40!, we have different powers of 5. For example, some numbers are divisible by \(5^1\) whereas we have number which is divisible by \(5^2\) also.
• Now, we know that the number 5 occurs in every five consecutive numbers. So, if we move from 1 to 40, we can find the instances of 5, by simply dividing 40 by 5.
• Similarly, we get an instance of 25 in every 25 consecutive numbers. So, if we move from 1 to 40, we can find the instances of 25, by dividing 40 by 25.
• Now, do we need to check for the other powers of 5?
- o \(5^3\) is 125, and in 40, we do not get an instance of 125. Hence, we do not need to check for \(5^3\) or further powers of 5.
So, now let’s divide 40 by \(5^1\) and \(5^2\), to determine their individual instances.
- • \(\frac{40}{5^1} = 8\)
• \(\frac{40}{5^2} = \frac{40}{25} = 1\)
\(5^1\) and \(5^2\) are the only two powers of 5 that can divide 40. Higher powers of 5 (for example, \(5^3\) = 125, or \(5^4\) = 625 etc.) are greater than 40, hence we will not consider them while dividing with powers of 5.
Therefore, the highest power of 5 in 40! = 8 + 1 = 9
In other words, we can also say that the greatest value of p, for which \(5^p\) is a factor of 40! Is 9.
So, the correct answer choice is option C.
Now, let’s solve one more similar question, to solidify our understanding.
Question 2
What is the highest power of 8, that can divide 88!?
- A. 11
B. 12
C. 25
D. 28
E. 29
Understanding the Question
This question is similar to the previous question that we solved a while ago. Hence, you may think that we can apply the same method here.
Let’s see what happens when we do that.
In this question, we are asked to find the highest power of 8 that can divide the number 88!
So, we must divide 88 by powers of 8, till division is possible, and then add the quotients to obtain the highest power of 8.
- • \(\frac{88}{8^1} = 11\)
• \(\frac{88}{8^2} = \frac{88}{64} = 1\)
As \(8^3 = 512\) is greater than 88, we don’t need to consider that.
Hence, the highest power of 8 that can divide 88! = 11 + 1 = 12
So, the correct answer choice is option B, right?
- • No, 12 is not the correct answer.
Let’s analyse the question a bit more to understand the error.
Approach & Solution
When we divide 88! by 8 or powers of 8, we are only identifying and counting those numbers which are multiples of 8, such as 24, 32, 56 etc.
But, are these numbers the only ones by which we can get as a multiple of 8?
- • Can we not get a multiple of 8 by multiplying a multiple of 2 and another multiple of 4?
- o Answer yourself.
• Now 44 is a multiple of 4 and 70 is a multiple of 2, hence, their product must be a multiple of 4 * 2 = 8, right?
- o But when we divide 88 by the powers of 8, we didn’t consider these numbers!
o Hence, just by dividing the number by 8, we may not get all such instances where we can get an 8 or its multiple.
In such cases, what should we do? We need to first express the number in the prime factorized form.
- • We know \(8 = 2 * 2 * 2 = 2^3\)
• Hence, if we get three 2's, then we can form an 8 from them. So, let’s find out the number of 2's first.
- o \(\frac{88}{2} + \frac{88}{2^2}+ \frac{88}{2^3} + \frac{88}{2^4} + \frac{88}{2^5} + \frac{88}{2^6} = 44 + 22 + 11 + 5 + 2 + 1 = 85\)
o Therefore, in 88! we have total 85 instances of 2.
o From these 85 instances of 2, we can make \(\frac{85}{3} = 28\) number of 8’s. (As 8 = 23, to form an 8, we need 3 instances of 2)
o Therefore, the highest power of 8 that can divide is 88! is 28. And the correct answer is option D.
Difference between Question 1 and Question 2
Well, we need to understand the fundamental difference between the two questions.
- • In question 1, we directly divided the number by 5 to get the instances of 5 in the factorial value. Whereas in question 2, we first prime factorized 8 and then calculated the instances of the prime factor in the factorial value.
"Whenever we need to calculate the instances of any prime number in a factorial value, we can do that by directly dividing the factorial number by the prime number. But, if we have a composite number, then first we need to express the number in terms of its prime factors. We need to prime factorize because apart from the number and its powers, we can get the instances of the number from the combination of other numbers also". (For example, we can get 8 by 4 * 2 or 2 * 2 * 2, apart from 8 or powers of 8)
Once we get the prime factor(s) of the number, we need to find the instances of each of the prime factor(s), and then from them, the instances of the original number.
Now, let’s solve another variation of the similar concept, on the applications of factorials.
Case 2
The Context
Sometimes we get questions where we are given a factorial number, and we need to find the number of consecutive zeroes at the end of the value of the number, before the first non-zero digit from the right. This is another interesting application of the same concept of factorials that we discussed in the previous two questions. Let’s demonstrate that with an example.
Question 3
How many trailing zeroes would be found in 57! upon expansion?
- A. 5
B. 13
C. 28
D. 53
E. 57
Understanding the Question
In this question, we are given a number 57! and we are asked to find the number of trailing 0's at the end of the value of 57!
The value of 57! is effectively a number which we get by multiplying all the positive integers from 1 to 57. But how do get 0's at the end of a product of two or more numbers?
- • We get 0's when we have presence of 10 or multiples of 10 in that product.
- o Hence, to find the number of trailing 0's, we need to know the instances of 10 in 57!
o Or in other words, we need to find the highest power of 10 that can divide 57!
Now, this is a known application to us – in the previous question, we solved the same only. So, let’s follow the same approach.
Approach & Solution
As 10 is a composite number, first we need to express it in terms of its prime factorized form.
- • As \(10 = 2^1 * 5^1\), we need to find the instances of 2 and 5 separately in 57! and then we can calculate the number of possible pairs of 2 and 5, to get the instances of 10.
• Instances of 2: \(\frac{57}{2^1} + \frac{57}{2^2}+ \frac{57}{2^3} + \frac{57}{2^4} + \frac{57}{2^5}= \frac{57}{2} + \frac{57}{4} + \frac{57}{8} + \frac{57}{16} + \frac{57}{32} = 28 + 14 + 7 + 3 + 1 = 53\)
• Similarly, instances of 5: \(\frac{57}{5^1} + \frac{57}{5^2} = \frac{57}{5} + \frac{57}{25} = 11 + 2 = 13\)
Now, we have 53 instances of 2's and 13 instances of 5's. We also know that, to form a 10, we need 1 instance of 2 and 1 instance of 5.
Hence, number of possible pairs of 2 and 5 = minimum (53, 13) = 13
Or, we can also say that the number of trailing 0's in 57! is 13.
Hence, the correct answer choice is option B.
Final Takeaways from the Article
- • If we are asked to find the highest power of a number ‘n’ in a factorial, where n is a prime number, we can directly divide the factorial number by ‘n’ (and possible powers of ‘n’) to find the instances of ‘n’, and subsequently the highest power of ‘n’.
- o In case n is a composite number, we must express ‘n’ first in the prime factorized form. From the prime factorized form, we need to find the instances of all individual prime factors, and finally instances of ‘n’.
• If we are asked to find the number of trailing zeroes in a factorial value, essentially, we are asked to find the highest power of 10 that can divide the factorial value. In such case, we can express 10 as 2 x 5, and find the individual instances of 2 and 5 respectively. Finally, we can find out how many possible pairs of 2 and 5 can be created, to calculate the highest power of 10.
Want to read more articles like this?
Now, if you liked this article, then I am sure that you want to read some more articles like this.
To read all our article go here: Must Read Articles and Practice Questions to score Q51 !!!!
You will also get a lot of practice questions to learn from.
Happy learning.
Attachments
![]() Variations in Factorial Manipulation.pdf [568.21 KiB]
Variations in Factorial Manipulation.pdf [568.21 KiB]
Downloaded 349 times
Kudos
Bookmarks
Thank you for posting a brilliant article on the factorial concept. Articles such as this one helps us brush our Quant concepts and the required skill set. Greatly appreciate the work.
Kudos
Bookmarks
Hey Everyone,
We've added 3 exercise questions in which you can apply your learnings of Factorial.
Exercise Questions
Question 1
Question 2
Question 3
Detailed solutions will be posted soon.
Happy Learning!
Regards,
Sandeep