gmat1220 wrote:
Karishma,
I have read your blog. Pls verify this - I am doing it intuitively.
If a - b > 0 this means at some point a = b. Lets determine that point. a = |2x+3| and b = |4-x|
Solving -
|2x+3| = |4-x|
Case 1
------
2x + 3 = 4 - x
3x = 1
x = 1/3
Therefore to make a > b, x > 1/3. i.e. move x further right of zero.
Case 2
-------
2x + 3 = x - 4
x + 7 = 0
x = -7
Therefore to make a > b, x < -7. i.e. move x further left of zero.
This is absolutely fine but I would not worry about equating... I would let common sense guide me... Let me tell you what I have in mind
Let's focus on just the x axis i.e. the number line
Since you have gone through the post, you know that mod is nothing but distance from 0 on the number line...
|x| = 2 means 'x is at a distance of 2 from point 0 on the number line'
|x-4| = 6 means 'the distance of x from 4 on the number line is 6' so x must be 10 or -2
These are the basics.
Let's take an easier example first. What does the following mean?
|x+2| > |x-4|
It means the value of x is such that distance from -2 is greater than distance from 4.
Attachment:
 Ques3.jpg [ 3.01 KiB | Viewed 6300 times ]
Ques3.jpg [ 3.01 KiB | Viewed 6300 times ]
Where is the distance from -2 equal to distance from 4? At point 1 on the number line, right? Red and green arrows will be equal.
So if x > 1, red arrow will be longer than green i.e. the distance of the point from -2 will be more than the distance from 4. So x > 1 satisfies this inequality.
What about points on the left of -2? Will there be any point such that its distance from -2 is equal to the distance from 4? Obviously not. All points will be closer to -2 than to 4.
Hence the only region is x > 1.
Now let's take the question at hand:
|2x+3| > |4-x|
2|x+3/2| > |x-4|
It means the value for x is such that twice the distance from -3/2 is more than the distance from 4.
Where will twice the distance from -1.5 be exactly equal to distance from 4?
Attachment:
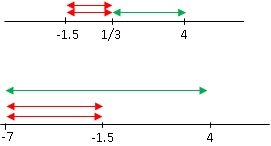 Ques2.jpg [ 7.97 KiB | Viewed 6304 times ]
Ques2.jpg [ 7.97 KiB | Viewed 6304 times ]
We should divide the distance of 5.5 between them in 3 equal parts to get 5.5/3
Now lets go 5.5/3 ahead of -1.5 to get -1.5+5.5/3 = 1/3. This is the point where twice the distance from -3/2 is equal to distance from 4. So you go to the right to make twice the distance from -3/2 greater than the distance from 4. So one solution is x > 1/3
Is there some other point where the same thing will happen?
Yes, at x = -7. How do I get it? because distance between -1.5 and 4 is 5.5
When I add this to the left of -1.5, I get point 7 which is where double the distance from -1.5 will be equal to distance from point 4. To the left of -7, twice the distance from -1.5 will be greater than the distance from 4.
So another solution is x < -7
It is much more intuitive and all you need to do is draw a number line and then reason it out. Let me warn you, it's not everyday that I come across people who are interested in and appreciate alternative strategies. So when I do get an audience, I tend to get a little out of hand... If it makes sense to you, go ahead and try it out.. let me know if you get stuck with anything.. if it doesn't make sense, ignore it...



