Last visit was: 09 May 2026, 22:30

It is currently 09 May 2026, 22:30

Toolkit

Practice Tests

Data Insights Questions

Data Sufficiency (DS)

GMAT Club Daily Prep

Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.

Customized
for You

we will pick new questions that match your level based on your Timer History

Track
Your Progress

every week, we’ll send you an estimated GMAT score based on your performance

Practice
Pays

we will pick new questions that match your level based on your Timer History

Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.

Go to My Error Log Learn more

Request Expert Reply

Confirm Cancel

Back to Forum

Create Topic

If angle BAD is a right angle, what is the length of side

1 2

Bunuel

Math Expert

Joined: 02 Sep 2009

Last visit: 09 May 2026

Posts: 110,221

Own Kudos:

813,935

Given Kudos: 106,145

Products:

Expert

Expert reply

Posts: 110,221

Kudos: 813,935

18 May 2016, 05:53

Kudos

Bookmarks

komalsudhir

Bunuel Thanks for your reply. Median from Angle BAD will divide the hypotenuse BD into two halves. And, from statement 1 we know that AC is perpendicular to BD so AC satisfies both conditions of being a perpendicular and a bisector. Therefore from these two conditions we know that Triangle BAD is isosceles triangle. Therefore, side AB is also 5 and it makes side BD as 5√2.

How do you know for (1) that AC is the median?

felippemed

Joined: 23 Jun 2009

Last visit: 27 Oct 2020

Posts: 122

Own Kudos:

867

Given Kudos: 138

Location: Brazil

GMAT 1: 470 Q30 V20 Verified score

GMAT 2: 620 Q42 V33 Verified score

Posts: 122

Kudos: 867

08 Nov 2016, 14:42

Kudos

Bookmarks

here is my two cents

Attachments

Foto.png [ 198.01 KiB | Viewed 3529 times ]

mbaapp1234

Joined: 23 Dec 2013

Last visit: 05 Jul 2019

Posts: 81

Own Kudos:

Given Kudos: 23

Location: United States (CA)

Schools: HBS '20 (D) Stanford '20 (D) Yale '21 (A$) Tuck '21 (A) Wharton '21 (A) Sloan '21 (A)

GMAT 1: 710 Q45 V41 Verified score

GMAT 2: 760 Q49 V44 Verified score

GPA: 3.76

Products:

Schools: HBS '20 (D) Stanford '20 (D) Yale '21 (A$) Tuck '21 (A) Wharton '21 (A) Sloan '21 (A)

GMAT 2: 760 Q49 V44 Verified score

Posts: 81

Kudos: 90

29 May 2017, 17:11

Kudos

Bookmarks

chiragatara

If angle BAD is a right angle, what is the length of side BD?

(1) AC is perpendicular to BD

(2) BC = CD

Show Spoiler

Official answer explanation:

Using statements 1 and 2, we know that AC is the perpendicular bisector of BD. This means that triangle BAD is an isosceles triangle so side AB must have a length of 5 (the same length as side AD). We also know that angle BAD is a right angle, so side BD is the hypotenuse of right isosceles triangle BAD. If each leg of the triangle is 5, the hypotenuse (using the Pythagorean theorem) must be 5 underroot 2.

Can someone kindly explainthe underlined portion?

The goal here is to find the length of side BD. Since it's DS, the problem is not drawn to scale.

Statement 1) AC is perpendicular to BD.

We don't know if BC = BD, so this statement is insufficient. There are many possible triangles here that would give a different length of BD.

Statement 2) BC = CD

We don't know if AC is perpendicular to BD, so knowing that the two sides are equal doesn't help us.

Statements 1+2) We know that AC is the perpendicular bisector of BD, so that means that the line AC forms two isosceles triangles (ACD and ACB). Since the sides of the height is equal to their bases and two each other, then that means the two triangles are congruent. Since they are congruent, BAD is an isosceles triangle and its base, the hypotenuse of the triangle in this case, is 5 \sqrt{2}

RedIndian

Joined: 29 Aug 2017

Last visit: 04 Aug 2019

Posts: 21

Own Kudos:

Given Kudos: 3

Location: India

Schools: Schulich Sept"19 (A)

GPA: 4

Schools: Schulich Sept"19 (A)

Posts: 21

Kudos: 6

08 Dec 2017, 00:14

Kudos

Bookmarks

Kekki

Isn't it that in an right angle triangle a perpenidcular line to hupothenuses (BC) halves the 90 degree triangle into 45° and 45° degrees?

Hi Bunuel,

Small question here

Since the AC divides the triangle into three similar triangles. and we have side AD as 5. Cant we calculate ACD as a pyth triplet, hence 3-4-5 and then
AC/BC=CD/AC. This would give us BC??

Bunuel

Math Expert

Joined: 02 Sep 2009

Last visit: 09 May 2026

Posts: 110,221

Own Kudos:

813,935

Given Kudos: 106,145

Products:

Expert

Expert reply

Posts: 110,221

Kudos: 813,935

08 Dec 2017, 02:19

Kudos

Bookmarks

RedIndian

Kekki

Isn't it that in an right angle triangle a perpenidcular line to hupothenuses (BC) halves the 90 degree triangle into 45° and 45° degrees?

Are you talking about the first statement? If yes, then are you saying that ACD is 3-4-5 right triangle? HOW do you know that? The fact that the length of a hypotenuse is 5 does NOT mean that it must necessarily be 3-4-5 type.

vanam52923

Joined: 17 Jul 2017

Last visit: 12 Jun 2025

Posts: 198

Own Kudos:

103

Given Kudos: 228

Posts: 198

Kudos: 103

18 Nov 2019, 02:11

Kudos

Bookmarks

Bunuel

chiragatara

If angle BAD is a right angle, what is the length of side BD?

(1) AC is perpendicular to BD

(2) BC = CD

Official answer explanation:

Using statements 1 and 2, we know that AC is the perpendicular bisector of BD. This means that triangle BAD is an isosceles triangle so side AB must have a length of 5 (the same length as side AD). We also know that angle BAD is a right angle, so side BD is the hypotenuse of right isosceles triangle BAD. If each leg of the triangle is 5, the hypotenuse (using the Pythagorean theorem) must be 5 underroot 2.

Can someone kindly explainthe underlined portion?

For such kind of graphic questions you MUST post the image. Next, please also do check the OA's when posting a question, OA for this one is C, not E.

Original question is below:

If angle BAD is a right angle, what is the length of side BD?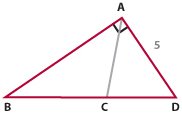

(1) AC is perpendicular to BD
(2) BC = CD

Now, obviously each statement alone is not sufficient.

When taken together we have that AC is a perpendicular bisector. Now, if a line from a vertex to the opposite side is both perpendicular to it and bisects it then this side is a base of an isosceles triangle (or in other words if a bisector and perpendicular coincide then we have an isosceles triangle). You can check this yourself: in triangles ACD and ACB two sides are equal (AC=AC and BC=CD) and included angle between these sides are also equal (<ACD=<ACB=90) so we have Side-Angle-Side case (SAS), which means that ACD and ACB are congruent triangles, so AB=AD --> ABD is an isosceles triangle.

Next, as ABD is an isosceles triangle then AB=AD=5 and hypotenuse $BD=5\sqrt{2}$.

Answer: C.

For more on this Triangles chapter of Math Book: https://gmatclub.com/forum/math-triangles-87197.html

Hope it helps.

Show Spoiler

Attachment:

triangleABCD.jpg

if angle A=60 then this traingle will be equilateral.right?

Also i have few doubts :
If the bisector of an angle in a triangle meets the opposite side at its midpoint, then the triangle is isosceles.?
is this correct .

or the bisector must meet the opposite side at mid point and at 90 degrees ( i.e. teh angle bisector line should be perp bisector of opposue side)

Plz clear

@chentan2u
Bunuel
plz xpln

Kritisood

Joined: 21 Feb 2017

Last visit: 19 Jul 2023

Posts: 488

Own Kudos:

1,320

Given Kudos: 1,090

Location: India

GMAT 1: 700 Q47 V39 Verified score

Products:

GMAT 1: 700 Q47 V39 Verified score

Posts: 488

Kudos: 1,320

23 Mar 2020, 04:27

Kudos

Bookmarks

Bunuel

BN1989

If AC is perpendicular to BD, then AC is the altitude from the right angle, isn't it? That would imply that triangles ABC and ACD are similar, so that angle CDA is equal to angle ABC, thus making triangle ABD an isoeleces right triangle and you could calculate BD then. What is wrong with that argumentation?

Yes, the perpendicular to the hypotenuse will always divide the triangle into two triangles with the same properties as the original triangle. But the corresponding (equal) angles would be BAC and ADC (also DAC and ABC) not CDA and ABC.

Hope it's clear.

Hi Bunuel

was doing a similar question a while back. Since AC is a perpendicular bisector BCA and DCA triangles would be similar. Next, how do I establish corresponding ratios? I have read the articles shared on this thread and the previous one, but I am not able to understand how to establish which sides are corresponding the respective equal angles. Any reading material available for this?

gmattaker2021

Joined: 06 Apr 2020

Last visit: 31 Mar 2026

Posts: 15

Own Kudos:

Given Kudos: 60

Posts: 15

Kudos: 1

20 Mar 2021, 08:29

Kudos

Bookmarks

Hey Bunuel,

As per statement 1, we can prove that triangles ACB and DCA are similar. We can also deduce that triangle ACD is a 30-60-90 triangle, thereby finding that AC=3, CD=4 and AD=5 (given). Hence applying h^2 (height)^2 = m*n ( AC^2=BC*BD), we could find that BC=9/4. Hence, BD=BC+CD, i.e, 9/4+4 = 25/4.

PS: I have seen the OA. Just want to understand what is wrong with my logic.

bumpbot

Non-Human User

Joined: 09 Sep 2013

Last visit: 04 Jan 2021

Posts: 39,042

Own Kudos:

1,123

Posts: 39,042

Kudos: 1,123

28 Aug 2023, 09:39

Kudos

Bookmarks

Automated notice from GMAT Club BumpBot:

A member just gave Kudos to this thread, showing it’s still useful. I’ve bumped it to the top so more people can benefit. Feel free to add your own questions or solutions.

This post was generated automatically.

1 2

Moderators:

Bunuel

Math Expert

110221 posts

kingbucky

498 posts

Gmat860sanskar

241 posts