metallicafan wrote:
In the xy-plane, region R consists of all the points (x,y) such that \(2x + 3y\leq{6}\). Is the point (r,s) in region R?
(1) \(3r + 2s = 6\)
(2) \(r\leq{3}\) and \(s\leq{2}\)
Target question:
Is the point (r, s) in region R? Given: Region R consists of all the points (x,y) such that 2x + 3y
<6
So, what does Region R look like?
To find out, let's first graph the EQUATION,
2x + 3y = 6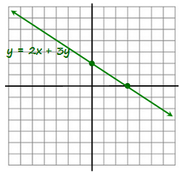
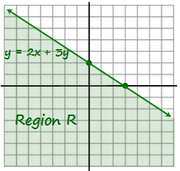
Since Region R is described as an INEQUALITY, we can choose any point on the coordinate plane to test whether or not it is in Region R. An easy point to test is (0,0).
So, does x=0 and y=0 satisfy the inequality 2x + 3y
<6? YES
2(0) + (3)(0) is less than or equal to 6.
So, the point (0,0) is in Region R. More importantly, EVERY POINT on the same side of the line will also be in Region R.
 Statement 1: 3r + 2s = 6
Statement 1: 3r + 2s = 6 The target question refers to the point (r, s)
In other words, the x-coordinate is r and the y-coordinate is s.
So, all of the points (r, s) that satisfy the above equation can be found on the line
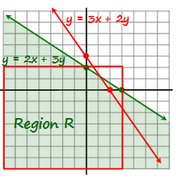
3x + 2y = 6In other words, statement 1 tells us that the point (r,s) lies somewhere on the red line below.
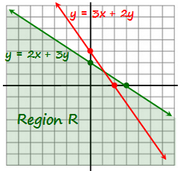
As you can see,
some points are in Region R, and
some points are not in Region RSince we cannot answer the
target question with certainty, statement 1 is NOT SUFFICIENT
Statement 2: r < 3 and s < 2 There are many points that satisfy this condition.
In fact, the point (r,s) can be ANYWHERE inside the red box shown below.
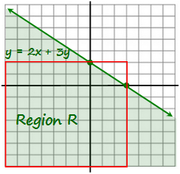
As you can see,
some points are in Region R, and
some points are not in Region RSince we cannot answer the
target question with certainty, statement 2 is NOT SUFFICIENT
Statements 1 and 2 combined When we combine the statements, we are saying that the point (r,s) is on the red line (2x + 3y = 6) AND inside the red box.
As you can see by the two blue points below, it's possible to have
a point in Region R, and it's possible to have
a point not in Region R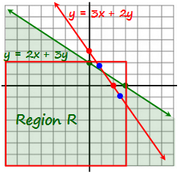
Since we cannot answer the
target question with certainty, the combined statements are NOT SUFFICIENT
Answer =
Cheers,
Brent



 95%
(hard)
95%
(hard)
 61%
(02:22)
wrong
61%
(02:22)
wrong  based on 5261
sessions
based on 5261
sessions












