Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 27 Nov 2016, 07:03.
Last edited by EgmatQuantExpert on 07 Aug 2018, 05:31, edited 26 times in total.
Last edited by EgmatQuantExpert on 07 Aug 2018, 05:31, edited 26 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
1. OBJECTIVE OF THE ARTICLE
Geometry is a topic with which a lot of students are not comfortable and many test takers avoid solving geometry questions.
There are two main reasons for this:
This article tries to address both the above issues by
The article is broadly divided into three sections
1. Basic Properties of a triangle:
This section covers the following aspects:
2. Tabular Representation:
Different types of triangles with their MOST important properties.
3. Special properties:
A few special properties that can be tested by GMAT.
Note: This post will cover just the first section!
So let’s get started!
2. BASIC PROPERTIES OF A TRIANGLE
2.1 CONCEPT 1
“Sum of lengths of any two sides of a triangle > Length of the third side”
Suppose you are given three lengths a, b, and c, and asked to find out if we can form a triangle using these three lengths.
How are you going to approach this problem?
Theory:
To determine if the three lengths will form a triangle or not, we need to know the most basic property of a triangle:
Sum of lengths of any two sides of a triangle > Length of the third side
This means that:
• a + b > c
• b + c > a
• c + a > b
Please note that all the three inequalities should satisfy for the triangle to exist.
Let us understand this with the help of a very basic GMAT-like question :
2.1.1 Illustrative Example 1
Q. The three lengths 5, 3, and x are used to form a triangle. Which of the following can be the value of x?
Solution
Since 5, 3 and x form a triangle, they must satisfy the property –
Sum of lengths of any two sides of a triangle > Length of the third side
Therefore, we can write :
So we can conclude that the range of x is: 2 < x < 8
Out of the given options, the only option that falls within this range is 6. Hence, Option A is our answer.
Therefore, now we know:
• How to find if the given lengths form a triangle or not
• How to use the above property to find the range of values for an unknown side in a triangle.
2.2 CONCEPT 2
“In any triangle, the largest side is always opposite the largest angle and the smallest side is always opposite the smallest angle.”
Suppose after finding out that the given lengths form a triangle, you want to find out how the length of the sides can help in finding a relation between the angles of the triangle.
To understand this, we need to know two more important properties –
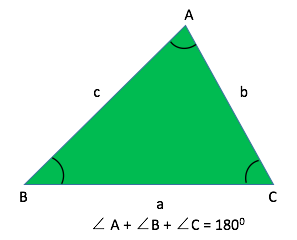
• The sum of the interior angles of a triangle is constant and is equal to \(180^o\).
Therefore,
• A + B + C = \(180^0\)
• Please note that the above property holds true for all triangles irrespective of their size and shape.
(notice I am using capital A, B and C to denote the angles of the triangle and a, b and c for the lengths of the sides of the triangle)
And another property is:
• In any triangle, the largest side is always opposite the largest angle and the smallest side is always opposite the smallest angle.
Let me explain this a bit more in detail:
If ABC is a triangle, in which we know that the lengths AB, BC, and CA follow the relation AB>BC>AC, then we can conclude that, since AB is the greatest side the angle opposite to it i.e., angle ACB is the greatest angle.
And since BC > AC, angles opposite to them also hold the same relation, that means
angle BAC > angle ABC
Hence we can conclude that: ∠ACB > ∠BAC > ∠ABC
Keep in mind that the converse is also true, i.e., if the relation between the angles is given, we can use that to find the relation between the sides.
Let us understand the application of this property through an example:
2.2.1 Illustrative Example 2:
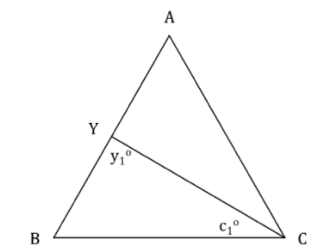
In the triangle given below, all the points denoted are non-overlapping and the angles A, B, and C are distinct. Is AB>AC>BC?
Solution:
Approach
We need to find if the statement AB > AC > BC is true or not.
For this, it is enough to get a relation among angles A, B and C since the sides of a triangle follow the same relation as the angles opposite to them.
Analyse Statement 1
y1 = c1
Therefore, in ΔBYC,
BY = BC
But AB = BY + YA
• AB > BC
However, we cannot infer any relationship between BC and AC (or AB and AC) from the given information.
Therefore, statement 1 is not sufficient to arrive at a unique answer.
Analyse Statement 2
Given angle BAC < angle ABC and neither angle is the greatest.
Also in the question statement it is mentioned that angles BAC, ABC, and ACB are distinct, therefore, angle ACB has to be the greatest angle.
Therefore, we can conclude, angle BAC < angle ABC < angle ACB
Thus, we can conclude that length BC < AC < AB
Hence, statement 2 is sufficient to arrive at a unique answer.
Correct Answer: B
This brings us to end of the first section of the article. I hope it was useful and informative. After reading this you should be able to easily -
The next sections of the article can be accessed using the following links:
Mastering Important Concepts Tested by GMAT in Triangles - Part 2
Mastering Important Concepts Tested by GMAT in Triangles - Part 3
NOTE: This is the second article in our Geometry series. If you liked the above article, you can also go through the link given below. I am sure you will find it useful
Common Mistakes in Geometry
Thanks,
Saquib
Quant Expert
e-GMAT
Mastering Important Concepts Tested by GMAT in Triangles- I
1. OBJECTIVE OF THE ARTICLE
Geometry is a topic with which a lot of students are not comfortable and many test takers avoid solving geometry questions.
There are two main reasons for this:
- i) There are too many concepts and formulae to remember. Even though GMAT tests us on a very limited number of properties, but since these limited properties are not collated in a single place, it is difficult for a test taker to confidently say he knows all the concepts.
ii) And say, even if someone manages to find and learn all the concepts, most of them are not sure how to apply these concepts to deduce information from the given question and figure in the questions tested on the GMAT
This article tries to address both the above issues by
- i) Consolidating the MOST important concepts needed in Triangles.
ii) Focusing on some GMAT-like and official questions and illustrating the application of the above concepts in these questions.
The article is broadly divided into three sections
1. Basic Properties of a triangle:
This section covers the following aspects:
- • Finding if a set of given numbers could be the lengths of a triangle or not,
• The range of values the side of a triangle can take given the values of the other two sides and
• The properties of the angles of the triangle.
2. Tabular Representation:
Different types of triangles with their MOST important properties.
3. Special properties:
A few special properties that can be tested by GMAT.
Note: This post will cover just the first section!
So let’s get started!
2. BASIC PROPERTIES OF A TRIANGLE
2.1 CONCEPT 1
“Sum of lengths of any two sides of a triangle > Length of the third side”
Suppose you are given three lengths a, b, and c, and asked to find out if we can form a triangle using these three lengths.
How are you going to approach this problem?
Theory:
To determine if the three lengths will form a triangle or not, we need to know the most basic property of a triangle:
Sum of lengths of any two sides of a triangle > Length of the third side
This means that:
• a + b > c
• b + c > a
• c + a > b
Please note that all the three inequalities should satisfy for the triangle to exist.
Let us understand this with the help of a very basic GMAT-like question :
2.1.1 Illustrative Example 1
Q. The three lengths 5, 3, and x are used to form a triangle. Which of the following can be the value of x?
- A. 6
B. 9
C. 10
D. 12
E. 14
Solution
Since 5, 3 and x form a triangle, they must satisfy the property –
Sum of lengths of any two sides of a triangle > Length of the third side
Therefore, we can write :
- I. 5+3 >x
x <8
II. 3 +x > 5
x > 2
III. 5 + x > 3
x > -2
So we can conclude that the range of x is: 2 < x < 8
Out of the given options, the only option that falls within this range is 6. Hence, Option A is our answer.
Therefore, now we know:
• How to find if the given lengths form a triangle or not
• How to use the above property to find the range of values for an unknown side in a triangle.
2.2 CONCEPT 2
“In any triangle, the largest side is always opposite the largest angle and the smallest side is always opposite the smallest angle.”
Suppose after finding out that the given lengths form a triangle, you want to find out how the length of the sides can help in finding a relation between the angles of the triangle.
To understand this, we need to know two more important properties –
• The sum of the interior angles of a triangle is constant and is equal to \(180^o\).
Therefore,
• A + B + C = \(180^0\)
• Please note that the above property holds true for all triangles irrespective of their size and shape.
(notice I am using capital A, B and C to denote the angles of the triangle and a, b and c for the lengths of the sides of the triangle)
And another property is:
• In any triangle, the largest side is always opposite the largest angle and the smallest side is always opposite the smallest angle.
Let me explain this a bit more in detail:
If ABC is a triangle, in which we know that the lengths AB, BC, and CA follow the relation AB>BC>AC, then we can conclude that, since AB is the greatest side the angle opposite to it i.e., angle ACB is the greatest angle.
And since BC > AC, angles opposite to them also hold the same relation, that means
angle BAC > angle ABC
Hence we can conclude that: ∠ACB > ∠BAC > ∠ABC
Keep in mind that the converse is also true, i.e., if the relation between the angles is given, we can use that to find the relation between the sides.
Let us understand the application of this property through an example:
2.2.1 Illustrative Example 2:
In the triangle given below, all the points denoted are non-overlapping and the angles A, B, and C are distinct. Is AB>AC>BC?
- I. angle y1 = angle c1
II. angle BAC < angle ABC and neither angle is the greatest in the triangle ABC
Solution:
Approach
We need to find if the statement AB > AC > BC is true or not.
For this, it is enough to get a relation among angles A, B and C since the sides of a triangle follow the same relation as the angles opposite to them.
Analyse Statement 1
y1 = c1
Therefore, in ΔBYC,
BY = BC
But AB = BY + YA
• AB > BC
However, we cannot infer any relationship between BC and AC (or AB and AC) from the given information.
Therefore, statement 1 is not sufficient to arrive at a unique answer.
Analyse Statement 2
Given angle BAC < angle ABC and neither angle is the greatest.
Also in the question statement it is mentioned that angles BAC, ABC, and ACB are distinct, therefore, angle ACB has to be the greatest angle.
Therefore, we can conclude, angle BAC < angle ABC < angle ACB
Thus, we can conclude that length BC < AC < AB
Hence, statement 2 is sufficient to arrive at a unique answer.
Correct Answer: B
This brings us to end of the first section of the article. I hope it was useful and informative. After reading this you should be able to easily -
- 1. apply Concept 1, to identify if a triangle can be formed from the given three lengths.
2. apply Concept 1, to also find the range of the unknown side, if the other two lengths of the triangle are given.
3. apply Concept 2 in questions where the relation of angles and sides are required to solve the problem.
The next sections of the article can be accessed using the following links:
Mastering Important Concepts Tested by GMAT in Triangles - Part 2
Mastering Important Concepts Tested by GMAT in Triangles - Part 3
NOTE: This is the second article in our Geometry series. If you liked the above article, you can also go through the link given below. I am sure you will find it useful
Common Mistakes in Geometry
Thanks,
Saquib
Quant Expert
e-GMAT
Attachments
![]() eGMAT Triangle-1.pdf [1.23 MiB]
eGMAT Triangle-1.pdf [1.23 MiB]
Downloaded 829 times
Originally posted by EgmatQuantExpert on 28 Nov 2016, 01:21.
Last edited by EgmatQuantExpert on 07 Aug 2018, 05:12, edited 2 times in total.
Last edited by EgmatQuantExpert on 07 Aug 2018, 05:12, edited 2 times in total.
Kudos
Bookmarks
Hey Everyone,
Please find below the link of 2 questions specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Detailed solutions will be posted soon.
Happy Learning!
Thanks,
Saquib
Quant Expert
e-GMAT
Please find below the link of 2 questions specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Detailed solutions will be posted soon.
Happy Learning!
Thanks,
Saquib
Quant Expert
e-GMAT
Originally posted by EgmatQuantExpert on 30 Nov 2016, 01:30.
Last edited by EgmatQuantExpert on 02 Dec 2016, 08:51, edited 1 time in total.
Last edited by EgmatQuantExpert on 02 Dec 2016, 08:51, edited 1 time in total.
Kudos
Bookmarks
Hey Everyone,
As promised, we have come up with the third article on the Geometry series.
Mastering Important Concepts Tested by GMAT in Triangles - Part 2
We have also posted two practice questions along with the article. Do give these questions a shot!
Thanks,
Saquib
As promised, we have come up with the third article on the Geometry series.
Mastering Important Concepts Tested by GMAT in Triangles - Part 2
We have also posted two practice questions along with the article. Do give these questions a shot!
Thanks,
Saquib