NEW HERE? LEARN MORE
closeclose
Last visit was: 26 Apr 2024, 05:06 It is currently 26 Apr 2024, 05:06
Decision Tracker
My Rewards
New posts
New comers' posts

Close
GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.

Customized
for You

we will pick new questions that match your level based on your Timer History

Track
Your Progress

every week, we’ll send you an estimated GMAT score based on your performance

Practice
Pays

we will pick new questions that match your level based on your Timer History
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Go to My Error Log Learn more
Close
Request Expert Reply
Confirm Cancel

The figure above shows a side view of the insert and the four componen

SORT BY:
Date
Kudos
Tags:
Find Similar Topics 
Show Tags
Hide Tags
User avatar
L
NandishSS
Director
Director
Joined: 06 Jan 2015
Posts: 738
Own Kudos [?]: 1586 [79]
Given Kudos: 579
Location: India
Concentration: Operations, Finance
GPA: 3.35
WE:Information Technology (Computer Software)
Send PM
The figure above shows a side view of the insert and the four componen [#permalink] New post   Updated on: 30 Jul 2016, 07:14
1
Kudos
77
Bookmarks
00:00
A
B
C
D
E

Difficulty:

75% (hard)

Question Stats:

59% (02:31) correct 41% (02:41) wrong based on 760 sessions
Hide Show timer Statistics

The figure above shows a side view of the insert and the four components of a box designed to package four lightbulbs. The package is a rectangular box, whose base is a square with a side of 8 inches and whose height is 12 inches. A single rectangular insert is folded twice to form two identical diagonal planes, one at each end, and a horizontal plane in the middle, so that the box is divided into four identical compartments. What is the area of the insert in square inches?

A) 192

B) 224

C) \(64+4\sqrt{52}\)

D) \(64+96\sqrt{2}\)

E) \(64+128\sqrt{2}\)

Show Spoiler
Attachment:
Figure.jpg
Figure.jpg [ 4.78 KiB | Viewed 27238 times ]
ShowHide Answer
Official Answer
B

Originally posted by NandishSS on 30 Jul 2016, 06:16.
Last edited by Bunuel on 30 Jul 2016, 07:14, edited 1 time in total.
Edited the question.
Most Helpful Reply
User avatar
L
KarishmaB
Tutor
Joined: 16 Oct 2010
Posts: 14828
Own Kudos [?]: 64931 [15]
Given Kudos: 427
Location: Pune, India
Send PM
Re: The figure above shows a side view of the insert and the four componen [#permalink] New post   13 Nov 2017, 04:47
11
Kudos
4
Bookmarks
Expert Reply
NandishSS wrote:

The figure above shows a side view of the insert and the four components of a box designed to package four lightbulbs. The package is a rectangular box, whose base is a square with a side of 8 inches and whose height is 12 inches. A single rectangular insert is folded twice to form two identical diagonal planes, one at each end, and a horizontal plane in the middle, so that the box is divided into four identical compartments. What is the area of the insert in square inches?

A) 192

B) 224

C) \(64+4\sqrt{52}\)

D) \(64+96\sqrt{2}\)

E) \(64+128\sqrt{2}\)

Show Spoiler
Attachment:
Figure.jpg


Too much of confusing explanation is given in the question which makes me think that the diagram tells it all. That is pretty much what the first sentence of the question says too.

We see the 8 x 12 rectangular box as shown in the figure.
A single rectangular insert is folded twice to make four identical compartments. We see in the figure that we have 4 identical right triangular compartments. So the insert is just the lightening shape shown in the figure. We need its area. It is actually a rectangle which is folded into this shape. If we open it up, we will get a rectangle and its area will be the total height * Width (which is 8 since the box has a square base of side 8)

Now all we need is the height. Since the compartments are equal, height of each compartment is 6. So each diagonal in the figure is 10 (using multiple of pythagorean triplet 3-4-5).
Total height of the rectangular insert = 10 + 8 + 10 = 28

Its area = 28*8 = 224
User avatar
L
CrackverbalGMAT
GMAT Club Legend
GMAT Club Legend
Joined: 03 Oct 2013
Affiliations: CrackVerbal
Posts: 4946
Own Kudos [?]: 7628 [10]
Given Kudos: 215
Location: India
Send PM
Re: The figure above shows a side view of the insert and the four componen [#permalink] New post   29 Mar 2022, 20:56
9
Kudos
1
Bookmarks
Top Contributor
tkorzhan1995 I hope the figure attached will help you to understand this question better.

Note: If you could visualize a 3D figure based on the information's given and understand what area we need to find here, solving this question would be easier.

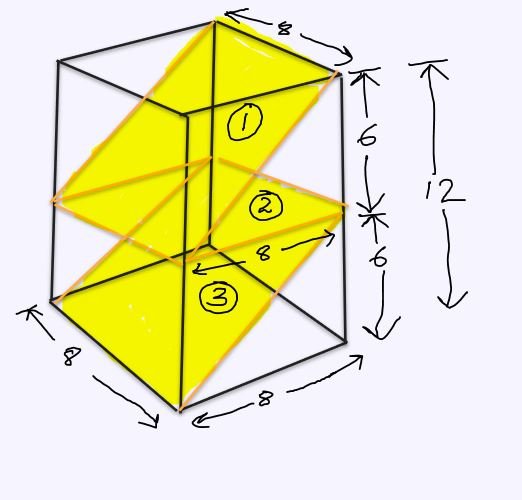
We have a rectangular box, whose base is a square with a side of 8 inches and whose height is 12 inches. A single rectangular sheet ( Yellow shaded region in the attached figure ) is folded twice to form two identical diagonal planes, one at each end, and a horizontal plane in the middle so that the box is divided into four identical compartments. We are asked to find the area of the rectangular insert.

Please refer to the figure attached for the 3D -view and we are asked to find the yellow shaded region in the figure.

Attachment:
3D_FIGURE.JPG
3D_FIGURE.JPG [ 38.36 KiB | Viewed 8106 times ]



Let's cut the entire rectangular insert into three parts: Sheets 1,2 and 3 as marked in the figure. The width of each sheet will be the same i.e 8 inches.

Since the box is divided into 4 identical compartments, the height of each compartment will be 12/2 = 6 inches.

The length of rectangular sheet 1 will be the hypotenuse of the right-angled triangle formed as shown in the figure with a base of 8 inches and a height of 6 inches.

Length of sheet 1 = Sq.root(\(8^2 + 6^2\)) = 10 inches

Area of Sheet 1 = 10 * 8 = 80 sq. inches

It's given in the question that Sheet 1 and Sheet 3 are two identical diagonal planes, hence their area will also be the same i.e 80 sq. inches.

Sheet 2 will be a square of base 8 cm, hence the area of sheet 2 = 8 * 8 = 64 sq. inches


Area of rectangular insert = Area of Sheet 1 + Area of sheet 2 + Area of sheet 3= 80 + 64 + 80 = 224 sq. inches.

Option B is the correct answer.

Thanks,
Clifin J Francis,
GMAT Mentor
General Discussion
User avatar
L
EMPOWERgmatRichC
GMAT Club Legend
GMAT Club Legend
Joined: 19 Dec 2014
Status:GMAT Assassin/Co-Founder
Affiliations: EMPOWERgmat
Posts: 21846
Own Kudos [?]: 11668 [8]
Given Kudos: 450
Location: United States (CA)
GMAT 1: 800 Q51 V49
GRE 1: Q170 V170
Send PM
Re: The figure above shows a side view of the insert and the four componen [#permalink] New post   30 Jul 2016, 13:19
5
Kudos
3
Bookmarks
Expert Reply
Hi NandishSS,

While this question looks complex, it's actually built around some fairly simple Geometry. It might help to break this calculation down into 'pieces' and think about the rules involved in this 3-dimensional shape.

To start, the 'insert' is a rectangle that's been folded in 2 spots. By definition, it has a length and a width; once we figure out those two dimensions, we can figure out its area.

We're meant to assume that the insert 'touches' the sides, so the width of the insert has to match the width of the box. Since the base of the box is an 8-inch square, the width of the insert is also 8 inches.

Next, we'll work on the 'middle' horizontal piece (it's the easiest part) - since it's horizontal, then it has the same length as the box (which is also 8 inches). Thus, that 'middle piece' is an 8x8 square = 64 in^2

The two diagonal pieces are the same length, so once we figure out one, we can double it and get the total area of those 2 'pieces.' You should notice how a bunch of right triangles are formed. The base of each of those triangles is 8 and the height is 6. This is a classic 3/4/5 right triangle that's been doubled to become a 6/8/10. Thus, the two diagonal pieces are 8x10 rectangles = 80 in^2 each.

64+80+80 = 224

Final Answer:
Show Spoiler
B


GMAT assassins aren't born, they're made,
Rich
User avatar
B
pthet9801
Intern
Intern
Joined: 18 Aug 2020
Posts: 2
Own Kudos [?]: 1 [0]
Given Kudos: 2
Concentration: Finance, Other
GMAT 1: 680 Q44 V39
GPA: 3.78
WE:Engineering (Energy and Utilities)
Send PM
Re: The figure above shows a side view of the insert and the four componen [#permalink] New post   06 Dec 2020, 20:04
I'm having trouble understanding why the area of the rectangular box wouldn't be: (10+8+6)*8? Isn't the right side of the triangle 6 in.? I'm missing where the other 10 in. comes from.
User avatar
L
EMPOWERgmatRichC
GMAT Club Legend
GMAT Club Legend
Joined: 19 Dec 2014
Status:GMAT Assassin/Co-Founder
Affiliations: EMPOWERgmat
Posts: 21846
Own Kudos [?]: 11668 [2]
Given Kudos: 450
Location: United States (CA)
GMAT 1: 800 Q51 V49
GRE 1: Q170 V170
Send PM
Re: The figure above shows a side view of the insert and the four componen [#permalink] New post   06 Dec 2020, 20:27
2
Kudos
Expert Reply
Hi pthet9801,

I assume that you're actually talking about the INSERT and not the BOX (since we're told the dimensions of the box - it's 8x8x12).

The insert can be broken down into 3 pieces: the two 'diagonal' sections and the middle 'horizontal' section. Since we're meant to assume that the insert 'touches' the sides, the width of the insert has to match the width of the box. The base of the box is an 8-inch square, so the width and length of the middle section is also 8x8 inches = 64 square inches.

The two diagonal pieces are the same length. You should notice how a bunch of right triangles are formed by those two pieces. The base of each of those triangles is 8 and since each 'pair' of triangles is HALF the height (re: half of 12 inches), the height of each triangle is 6 inches. This is a classic 3/4/5 right triangle that's been doubled to become a 6/8/10. Thus, the two diagonal pieces have a width of 8 inches and a length of 10 inches = 80 square inches each.

If you wanted to form a calculation in the way that you did in your post, then it would be (8+10+10)(8).

GMAT assassins aren't born, they're made,
Rich
User avatar
L
chetan2u
RC & DI Moderator
Joined: 02 Aug 2009
Status:Math and DI Expert
Posts: 11179
Own Kudos [?]: 31943 [1]
Given Kudos: 290
Send PM
Reviews Badge
Re: The figure above shows a side view of the insert and the four componen [#permalink] New post   30 Mar 2022, 01:35
1
Kudos
Expert Reply
NandishSS wrote:

The figure above shows a side view of the insert and the four components of a box designed to package four lightbulbs. The package is a rectangular box, whose base is a square with a side of 8 inches and whose height is 12 inches. A single rectangular insert is folded twice to form two identical diagonal planes, one at each end, and a horizontal plane in the middle, so that the box is divided into four identical compartments. What is the area of the insert in square inches?

A) 192

B) 224

C) \(64+4\sqrt{52}\)

D) \(64+96\sqrt{2}\)

E) \(64+128\sqrt{2}\)

Show Spoiler
Attachment:
The attachment Figure.jpg is no longer available



CrackverbalGMAT is absolutely correct with the sketch.

I will add on to it a bit

INSERT is the cardboard which is placed inside ( Red in colour ).
Partitions are equal so ABCD gives us the length of the partition as the entire INSERT is made by folding the rectagular cardboard at two places - B and C.

AB=CD= hypotenuse with other two sides 6 and 8, so both are 10.

Thus the insert becomes a rectangular piece with sides 8 and 10+8+10 as shown in the third sketch.
Area = 8*28 = 224

B
Attachments

UntitledA.png
UntitledA.png [ 35.23 KiB | Viewed 7496 times ]

GMAT Club Bot
gmatclubot
Re: The figure above shows a side view of the insert and the four componen [#permalink]
30 Mar 2022, 01:35
Moderators:
Bunuel
Math Expert
92929 posts
yashikaaggarwal
Senior Moderator - Masters Forum
3137 posts

Powered by phpBB © phpBB Group | Emoji artwork provided by EmojiOne
Main navigation
GMAT Resources
Partners
MBA Resources
www.gmac.com|www.mba.com | | GMAT Club Rules | Terms and Conditions