Forum Home > GMAT > Quantitative > Problem Solving (PS)
Events & Promotions
| Last visit was: 26 Jul 2024, 16:34 |
It is currently 26 Jul 2024, 16:34 |

Customized
for You
Track
Your Progress
Practice
Pays
10:00 AM PDT
-11:00 AM PDT
11:00 AM IST
-01:00 PM IST
08:00 AM EDT
-11:59 PM EDT
10:00 AM PDT
-11:00 AM PDT
11:00 AM IST
-01:00 PM IST
05:55 AM PDT
-12:30 PM PDT
10:00 AM EDT
-11:59 PM PDT
Difficulty:


 35%
(medium)
35%
(medium)
Question Stats:
74% (01:59) correct 26%
(01:48)
wrong
26%
(01:48)
wrong  based on 1099
sessions
based on 1099
sessions


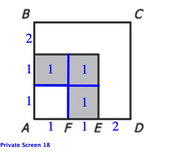

|
|
|
|