PROBABILITYThis post is a part of [
GMAT MATH BOOK]
created by: walkeredited by: bb,
Bunuel--------------------------------------------------------
Get The Official GMAT Club's App -
GMAT TOOLKIT 2.
The only app you need to get 700+ score!
[
iOS App] [
Android App]
--------------------------------------------------------
DefinitionA number expressing the probability (p) that a specific event
will occur, expressed as the ratio of the number of actual occurrences (n) to the number of possible occurrences (N).
\(p = \frac{n}{N}\)
A number expressing the probability (q) that a specific event
will not occur:
\(q = \frac{(N-n)}{N} = 1 - p\)
ExamplesCoin
There are two equally possible outcomes when we toss a coin: a head (H) or tail (T). Therefore, the probability of getting head is 50% or \(\frac{1}{2}\) and the probability of getting tail is 50% or \(\frac{1}{2}\).
All possibilities: {H,T}
Dice
There are 6 equally possible outcomes when we roll a die. The probability of getting any number out of 1-6 is \(\frac{1}{6}\).
All possibilities: {1,2,3,4,5,6}
Marbles, Balls, Cards...
Let's assume we have a jar with 10 green and 90 white marbles. If we randomly choose a marble, what is the probability of getting a green marble?
The number of all marbles: N = 10 + 90 =100
The number of green marbles: n = 10
Probability of getting a green marble: \(p = \frac{n}{N} = \frac{10}{100} = \frac{1}{10}\)
There is one important concept in problems with marbles/cards/balls. When the first marble is removed from a jar and not replaced, the probability for the second marble differs (\(\frac{9}{99}\) vs. \(\frac{10}{100}\)). Whereas in case of a coin or dice the probabilities are always the same (\(\frac{1}{6}\) and \(\frac{1}{2}\)). Usually, a problem explicitly states: it is a problem
with replacement or without replacement.
Independent eventsTwo events are independent if occurrence of one event does not influence occurrence of other events. For n independent events the probability is the product of all probabilities of independent events:
p = p1 * p2 * ... * pn-1 * pn
or
P(A and B) = P(A) * P(B) - A and B denote independent events
Example #1Q:There is a coin and a die. After one flip and one toss, what is the probability of getting heads and a "4"?
Solution: Tossing a coin and rolling a die are independent events. The probability of getting heads is \(\frac{1}{2}\) and probability of getting a "4" is \(\frac{1}{6}\). Therefore, the probability of getting heads and a "4" is:
\(P = \frac{1}{2} * \frac{1}{6} = \frac{1}{12}\)
Example #2Q: If there is a 20% chance of rain, what is the probability that it will rain on the first day but not on the second?
Solution: The probability of rain is 0.2; therefore probability of sunshine is q = 1 - 0.2 = 0.8. This yields that the probability of rain on the first day and sunshine on the second day is:
P = 0.2 * 0.8 = 0.16
Example #3Q:There are two sets of integers: {1,3,6,7,8} and {3,5,2}. If Robert chooses randomly one integer from the first set and one integer from the second set, what is the probability of getting two odd integers?
Solution: There is a total of 5 integers in the first set and 3 of them are odd: {1, 3, 7}. Therefore, the probability of getting odd integer out of first set is \(\frac{3}{5}\). There are 3 integers in the second set and 2 of them are odd: {3, 5}. Therefore, the probability of getting an odd integer out of second set is \(\frac{2}{3}\). Finally, the probability of of getting two odd integers is:
\(P = \frac{3}{5} * \frac{2}{3} = \frac{2}{5}\)
Mutually exclusive eventsShakespeare's phrase "To be, or not to be: that is the question" is an example of two mutually exclusive events.
Two events are mutually exclusive if they cannot occur at the same time. For n mutually exclusive events the probability is the sum of all probabilities of events:
p = p1 + p2 + ... + pn-1 + pn
or
P(A or B) = P(A) + P(B) - A and B denotes mutually exclusive events
Example #1Q: If Jessica rolls a die, what is the probability of getting at least a "3"?
Solution: There are 4 outcomes that satisfy our condition (at least 3): {3, 4, 5, 6}. The probability of each outcome is 1/6. The probability of getting at least a "3" is:
\(P = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{2}{3}\)
Combination of independent and mutually exclusive eventsMany probability problems contain combination of both independent and mutually exclusive events. To solve those problems it is important to identify all events and their types. One of the typical problems can be presented in a following general form:
Q: If the probability of a certain event is p, what is the probability of it occurring k times in n-time sequence?
(Or in English, what is the probability of getting 3 heads while tossing a coin 8 times?)
Solution: All events are independent. So, we can say that:
\(P' = p^k*(1-p)^{n-k}\) (1)
But it isn't the right answer. It would be right if we specified exactly each position for events in the sequence. So, we need to take into account that there are more than one outcomes. Let's consider our example with a coin where "H" stands for Heads and "T" stands for Tails:
HHHTTTTT and HHTTTTTH are different mutually exclusive outcomes but they both have 3 heads and 5 tails. Therefore, we need to include all combinations of heads and tails. In our general question, probability of occurring event k times in n-time sequence could be expressed as:
\(P = C^n_k*p^k*(1-p)^{n-k}\) (2)
In the example with a coin, right answer is \(P = C^8_3*0.5^3*0.5^5 =C^8_3*0.5^8\)
Example #1Q.:If the probability of raining on any given day in Atlanta is 40 percent, what is the probability of raining on exactly 2 days in a 7-day period?
Solution: We are not interested in the exact sequence of event and thus apply formula #2:
\(P = C^7_2*0.4^2*0.6^5\)
A few ways to approach a probability problemThere are a few typical ways that you can use for solving probability questions. Let's consider example, how it is possible to apply different approaches:
Example #1Q: There are 8 employees including Bob and Rachel. If 2 employees are to be randomly chosen to form a committee, what is the probability that the committee includes both Bob and Rachel?
Solution:
1) combinatorial approach: The total number of possible committees is \(N=C^8_2\). The number of possible committee that includes both Bob and Rachel is \(n=1\).
\(P = \frac{n}{N} = \frac{1}{C^8_2} = \frac{1}{28}\)
2) reversal combinatorial approach: Instead of counting probability of occurrence of certain event, sometimes it is better to calculate the probability of the opposite and then use formula p = 1 - q. The total number of possible committees is \(N=C^8_2\). The number of possible committee that does not includes both Bob and Rachel is:
\(m = C^6_2 + 2*C^6_1\) where,
\(C^6_2\) - the number of committees formed from 6 other people.
\(2*C^6_1\) - the number of committees formed from Rob or Rachel and one out of 6 other people.
\(P = 1- \frac{m}{N} = 1 - \frac{C^6_2 + 2*C^6_1}{C^8_2}\)
\(P = 1 - \frac{15+2*6}{28} = 1 - \frac{27}{28} = \frac{1}{28}\)
3) probability approach: The probability of choosing Bob or Rachel as a first person in committee is 2/8. The probability of choosing Rachel or Bob as a second person when first person is already chosen is 1/7. The probability that the committee includes both Bob and Rachel is.
\(P = \frac{2}{8} * \frac{1}{7} = \frac{2}{56} = \frac{1}{28}\)
4) reversal probability approach: We can choose any first person. Then, if we have Rachel or Bob as first choice, we can choose any other person out of 6 people. If we have neither Rachel nor Bob as first choice, we can choose any person out of remaining 7 people. The probability that the committee includes both Bob and Rachel is.
\(P = 1 - (\frac{2}{8} * \frac{6}{7} + \frac{6}{8} * 1) = \frac{2}{56} = \frac{1}{28}\)
Example #2Q: Given that there are 5 married couples. If we select only 3 people out of the 10, what is the probability that none of them are married to each other?
Solution:
1) combinatorial approach:
\(C^5_3\) - we choose 3 couples out of 5 couples.
\(C^2_1\) - we chose one person out of a couple.
\((C^2_1)^3\) - we have 3 couple and we choose one person out of each couple.
\(C^{10}_3\) - the total number of combinations to choose 3 people out of 10 people.
\(p=\frac{C^5_3*(C^2_1)^3}{C^{10}_3}=\frac{10*8}{10*3*4} = \frac{2}{3}\)
2) reversal combinatorial approach: In this example reversal approach is a bit shorter and faster.
\(C^5_1\) - we choose 1 couple out of 5 couples.
\(C^8_1\) - we chose one person out of remaining 8 people.
\(C^{10}_3\) - the total number of combinations to choose 3 people out of 10 people.
\(p=1 - \frac{C^5_1*C^8_1}{C^{10}_3}=1 - \frac{5*8}{10*3*4} = \frac{2}{3}\)
3) probability approach:
1st person: \(\frac{10}{10} = 1\) - we choose any person out of 10.
2nd person: \(\frac{8}{9}\) - we choose any person out of 8=10-2(one couple from previous choice)
3rd person: \(\frac{6}{8}\) - we choose any person out of 6=10-4(two couples from previous choices).
\(p = 1*\frac{8}{9}*\frac{6}{8}=\frac{2}{3}\)
Probability treeSometimes, at 700+ level you may see complex probability problems that include conditions or restrictions. For such problems it could be helpful to draw a probability tree that include all possible outcomes and their probabilities.
Example #1Q: Julia and Brian play a game in which Julia takes a ball and if it is green, she wins. If the first ball is not green, she takes the second ball (without replacing first) and she wins if the two balls are white or if the first ball is gray and the second ball is white. What is the probability of Julia winning if the jar contains 1 gray, 2 white and 4 green balls?
Solution: Let's draw all possible outcomes and calculate all probabilities.
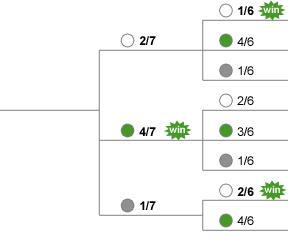
Now, It is pretty obvious that the probability of Julia's win is:
\(P = \frac47 + \frac27*\frac16 + \frac17*\frac26 = \frac23\)
Tips and Tricks: SymmetrySymmetry sometimes lets you solve seemingly complex probability problem in a few seconds. Let's consider an example:
Example #1Q: There are 5 chairs. Bob and Rachel want to sit such that Bob is always left to Rachel. How many ways it can be done ?
Solution: Because of symmetry, the number of ways that Bob is left to Rachel is exactly 1/2 of all possible ways:
\(N = \frac12*P^5_2 = 10\)
Official GMAC Books:The Official Guide, 12th Edition: DT #4; DT #7; PS #12; PS #67; PS #105; PS #158; PS #174; PS #214; DS #3; DS #107;
The Official Guide, Quantitative 2th Edition: PS #79; PS #160;
The Official Guide, 11th Edition: DT #4; DT #7; PS #10; PS #64; PS #173; PS #217; PS #231; DS #82; DS #114;
Generated from [
GMAT ToolKit 2]
ResourcesProbability DS problems: [
search]
Probability PS problems: [
search]
Walker's post with Combinatorics/probability problems: [
Combinatorics/probability Problems]
Bullet's post with probability problems: [
Combined Probability Questions]
--------------------------------------------------------
Get The Official GMAT Club's App -
GMAT TOOLKIT 2.
The only app you need to get 700+ score!
[
iOS App] [
Android App]
--------------------------------------------------------
Attachment: 
Math_probability_I_head.png [ 31.29 KiB | Viewed 187707 times ]
| Attachment: 
Math_probability_I_tail.png [ 32.04 KiB | Viewed 187492 times ]
| Attachment: 
Math_probability_I_dice.png [ 12.38 KiB | Viewed 187267 times ]
| Attachment: 
Math_probability_I_marbles.png [ 31.81 KiB | Viewed 187156 times ]
|
Attachment: 
Math_probability_tree.png [ 9.84 KiB | Viewed 186857 times ]
Attachment: 
Math_icon_probability.png [ 4.65 KiB | Viewed 182559 times ]
| | |
_________________
HOT! GMAT TOOLKIT 2 (iOS) / GMAT TOOLKIT (Android) - The OFFICIAL GMAT CLUB PREP APP, a must-have app especially if you aim at 700+ | PrepGame
close
