STANDARD DEVIATIONDefinitionStandard Deviation (SD, or STD or \(σ\)) - a measure of the dispersion or variation in a distribution, equal to the
square root of variance or the arithmetic mean (average) of squares of deviations from the arithmetic mean.
\(variance = \frac{\sum(x_i - x_{av})^2}{N}\)
\(σ= \sqrt{variance} = \sqrt{\frac{\sum(x_i - x_{av})^2}{N}}\)
In simple terms, it shows how much variation there is from the "average" (mean). It may be thought of as the average difference from the mean of distribution, how far data points are away from the mean. A low standard deviation indicates that data points tend to be very close to the mean, whereas high standard deviation indicates that the data are spread out over a large range of values.
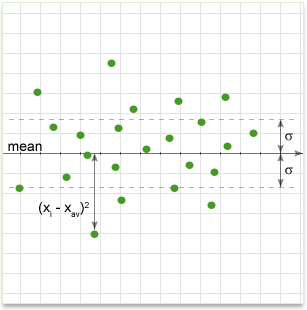
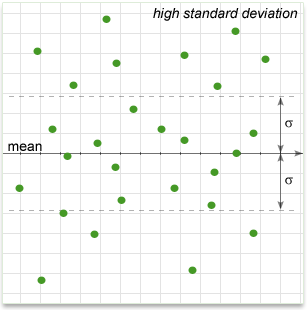
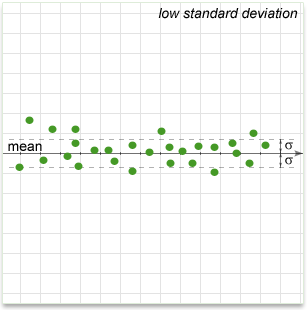 Properties
Properties\(σ \ge 0\);
\(σ = 0\) only if
all elements in a set is equal;
Let standard deviation of \(\{x_i\}\) be \(σ\) and mean of the set be \(m\):
Standard deviation of \(\{\frac{x_i}{a}\}\) is \(σ^{'}=\frac{σ}{a}\). Decrease/increase in all elements of a set by a constant percentage will decrease/increase standard deviation of the set by the same percentage.
Standard deviation of \(\{x_i+a\}\) is \(σ^{'}=σ\). Decrease/increase in all elements of a set by a constant value DOES NOT decrease/increase standard deviation of the set.
if a new element \(y\) is added to \(\{x_i\}\) set and standard deviation of a new set \(\{\{x_i\},y\}\) is \(σ^{'}\), then:
1) \(σ^{'} > σ\) if \(|y-m|>σ\)
2) \(σ^{'} = σ\) if \(|y-m|=σ\)
3) \(σ^{'} < σ\) if \(|y-m|<σ\)
4) \(σ^{'}\) is the lowest if \(y=m\)
Tips and TricksGMAC in majority of problems doesn't ask you to calculate standard deviation. Instead it tests your intuitive understanding of the concept. In 90% cases it is a faster way to use just average of \(|x_i-x_{av}|\) instead of true formula for standard deviation, and treat standard deviation as "
average difference between elements and mean". Therefore, before trying to calculate standard deviation, maybe you can solve a problem much faster by using just your intuition.
Advance tip. Not all points contribute equally to standard deviation. Taking into account that standard deviation uses sum of squares of deviations from mean, the most remote points will essentially contribute to standard deviation. For example, we have a set A that has a mean of 5. The point 10 gives \((10-5)^2=25\) in sum of squares but point 6 gives only \((6-5)^2=1\). 25 times the difference! So, when you need to find what set has the largest standard deviation, always look for set with the largest range because remote points have a very significant contribution to standard deviation.
ExamplesExample #1Q: There is a set \(\{67,32,76,35,101,45,24,37\}\). If we create a new set that consists of all elements of the initial set but decreased by 17%, what is the change in standard deviation?
Solution: We don't need to calculate as we know rule that decrease in all elements of a set by a constant percentage will decrease standard deviation of the set by the same percentage. So, the decrease in standard deviation is 17%.
Example #2Q: There is a set of consecutive even integers. What is the standard deviation of the set?
(1) There are 39 elements in the set.
(2) the mean of the set is 382.
Solution: Before reading Data Sufficiency statements, what can we say about the question? What should we know to find standard deviation? "consecutive even integers" means that all elements strictly related to each other. If we shift the set by adding or subtracting any integer, does it change standard deviation (average deviation of elements from the mean)? No. One thing we should know is the number of elements in the set, because the more elements we have the broader they are distributed relative to the mean. Now, look at DS statements, all we need it is just first statement. So, A is sufficient.
Example #3Q: Standard deviation of set \(\{23,31,76,45,16,55,54,36\}\) is 18.3. How many elements are 1 standard deviation above the mean?
Solution: Let's find mean: \(m=\frac{23+31+76+45+16+55+54+36}{8}=42\)
Now, we need to count all numbers greater than 42+18.3=60.3. It is one number - 76. The answer is 1.
Example #4Q: There is a set A of 19 integers with mean 4 and standard deviation of 3. Now we form a new set B by adding 2 more elements to the set A. What two elements will decrease the standard deviation the most?
A) 9 and 3
B) -3 and 3
C) 6 and 1
D) 4 and 5
E) 5 and 5
Solution: The closer to the mean, the greater decrease in standard deviation. D has 4 (equal our mean) and 5 (differs from mean only by 1). All other options have larger deviation from mean.
Normal distributionIt is a more advance concept that you will never see in GMAT but understanding statistic properties of standard deviation can help you to be more confident about simple properties stated above.
In probability theory and statistics, the normal distribution or Gaussian distribution is a continuous probability distribution that describes data that cluster around a mean or average. Majority of statistical data can be characterized by normal distribution.
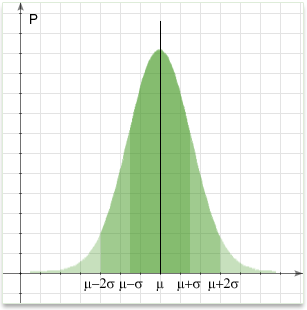
\(m-σ < x < m + σ\) covers 68% of data
\(m-2σ < x < m + 2σ\) covers 95% of data
\(m-3σ < x < m + 3σ\) covers 99% of data
Practice QuestionsEasy:Medium:Hard:
Attachment:
 Math_SD_graph.png [ 6.04 KiB | Viewed 201616 times ]
Math_SD_graph.png [ 6.04 KiB | Viewed 201616 times ]
Attachment:
 Math_SD_graph_low.png [ 5.92 KiB | Viewed 201472 times ]
Math_SD_graph_low.png [ 5.92 KiB | Viewed 201472 times ]
Attachment:
 Math_SD_graph_high.png [ 7.06 KiB | Viewed 201551 times ]
Math_SD_graph_high.png [ 7.06 KiB | Viewed 201551 times ]
Attachment:
 Math_SD_normal.png [ 7.67 KiB | Viewed 200533 times ]
Math_SD_normal.png [ 7.67 KiB | Viewed 200533 times ]
Attachment:
 Math_icon_std.png [ 2.67 KiB | Viewed 199290 times ]
Math_icon_std.png [ 2.67 KiB | Viewed 199290 times ]




