Events & Promotions
|
|
GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
May 1810:00 AM PDT
-11:00 AM PDT
Join us in a live GMAT practice session and solve 25 challenging GMAT questions with other test takers in timed conditions, covering GMAT Quant, Data Sufficiency, Data Insights, Reading Comprehension, and Critical Reasoning questions.
May 1212:00 PM EDT
-11:59 PM EDT
Make the most of your break with the most realistic GMAT™ prep. Take up to $700 off select products. Ends 6/1
May 1501:00 PM IST
-11:00 AM IST
Start your journey with a fully customized action plan and work with a dedicated mentor to achieve a 735+ score.- May 19
12:00 PM PDT
-01:00 PM PDT
Scoring 329 on the GRE is not always about using more books, more courses, or a longer study plan. In this episode of GRE Success Talks, Ashutosh shares his GRE preparation strategy, study plan, and test-day experience, explaining how he kept his prep.... - Jun 10
06:00 AM PDT
-06:15 PM PDT
Register for the GMAT Club Virtual MBA Spotlight Fair – the world’s premier event for serious MBA candidates. This is your chance to hear directly from Admissions Directors at nearly every Top 30 MBA program..
souvik101990
Expert
Alum
Joined: 19 Mar 2012
Last visit: 11 Nov 2025
Posts: 4,312
Given Kudos: 2,326
Location: United States (WA)
Concentration: Leadership, General Management
Schools: Ross '20 (M)
GMAT 1: 760 Q50 V42
GMAT 2: 740 Q49 V42 (Online)
GMAT 3: 760 Q50 V42 (Online)
GPA: 3.8
WE:Marketing (Non-Profit and Government)
Products:
Expert reply
23 Sep 2018, 14:21
Kudos
Bookmarks
N
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
(N/A)
Question Stats:
0% (00:00) correct
0%
(00:00)
wrong
based on 0
sessions
History
Date
Time
Result
Not Attempted Yet
GMAT Tip of the Week: Tips and Tricks for Absolute Values
This topic is a part of the GMAT Club Tip of the Week Series
YouTube Link: https://www.youtube.com/watch?v=O12sYaubFBo
This topic is a part of the GMAT Club Tip of the Week Series
YouTube Link: https://www.youtube.com/watch?v=O12sYaubFBo
To score beyond Q49 on GMAT, it is very important that you master Algebra as it has significant application in other sections such as Number Properties, Word Problems and Geometry. In this article, we would help learn you a simple yet effective approach to solve questions on one of the most confusing topics in Algebra - Absolute Value equations. Then we share a link with you to learn Absolute Inequalities, so that you can solve any Absolute value question with ease.
We suggest that you follow the sequence mentioned below:
- 1. Get started by going through the video lessons embedded above to learn the basics.
2. Then go through the following questions in this article to learn how to solve Absolute Equation questions that involve multiple modulus.
3. Finally go through the concept of Absolute Inequalities, to continue learning.
e-GMAT Example 1
If x is an integer, then find the values of x that satisfy the equation ||x + 9| - 15| = 10?
Solution
As we can see that we are given one modulus inside another modulus:
- o That is, |x+9| is inside ||x+9|-15|.
o And, we are asked to find out all the possible values of x such that ||x + 9| - 15| = 10.
So, how do we solve this question?
- o Well, we will simply apply the basic properties of absolute values.
- 1. We will first solve the outermost modulus.
- a. And, while solving it, we can substitute the inner modulus with an appropriate variable such as y.
3. Now, this process will continue even if we had more than 2 moduli in the question.
- a. We will first solve the outermost and then we move from outermost modulus to the inner moduli.
So, let's apply the same process here.
- o We will start from the outer modulus.
- o Therefore, let us substitute the inner modulus, |x+9|= y.
- Hence, we get |y - 15| = 10.
o Now, let's focus our energy on solving the equation |y - 15| = 10
- From the concept video, we learnt that the form |x - a| = b represents numbers on the number line that are at a distance of 'b' units from 'a'
Applying this logic, to the equation |y - 15| = 10, we can say that y is a number at a distance of 10 units from "15".
o So, let's find out all the numbers, which are at a distance of 10 units from the point '15', by representing it on a number line.
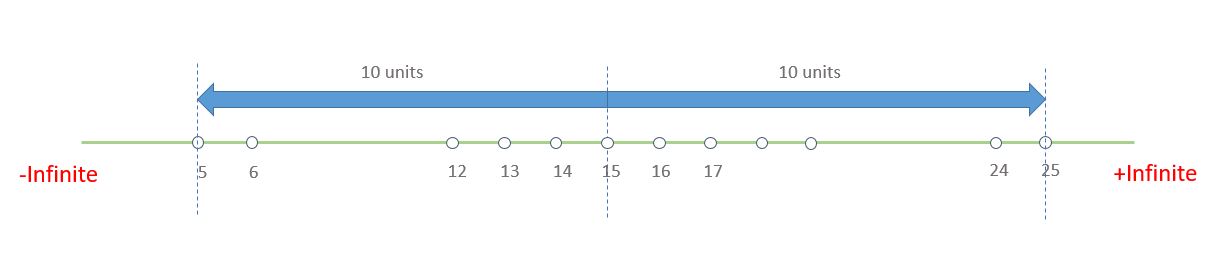
- o If we observe the diagram above, we can notice that there can be two possible numbers, which are at a distance of 10 units from 15.
- One on the left side of 15, which is 10 units away from it = 15 - 10 = 5 and
One on the right side of 15, which is 10 units away from it = 15 + 10 = 25
o Hence, the possible values of y are 5 and 25
o Substituting back the modulus in the above equation, we get,
- |x + 9| = 5, or
|x + 9| = 25
o Let's solve each modulus individually and find the values of x
o Considering the first case, where |x + 9| = 5, we need to find the values of x, which are at a distance of 5 units from -9.
- Now, most of you might wonder, why did we consider -9, instead of 9. But, if we observe the general equation of modulus carefully, it is of the form |x - a| = b., where x is b units away from point 'a'.
And, in this case, we can write |x + 9| = 5 as |x - (-9) | = 5.
Note: So, remember to notice the sign of 'a' carefully as it is a common mistake done by users and you would find one of the answer choices to set you up in this trap.
So, representing -9 on a number line, we can find that the numbers, which are at a distance of 5 units from -9 are -14 and -4
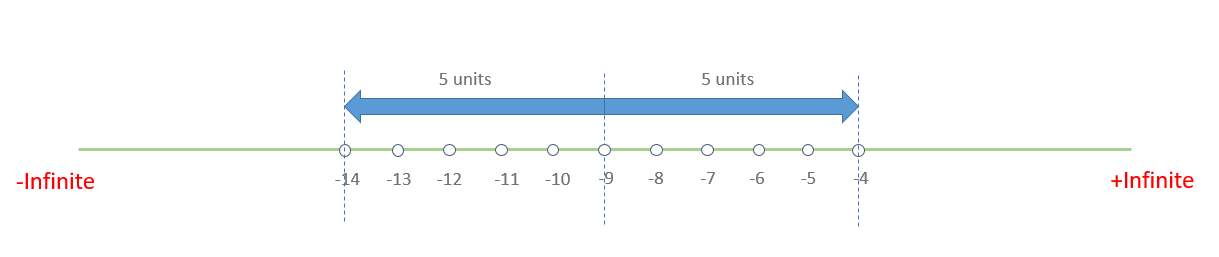
- Thus, the values of x that satisfy the equation, |x + 9| = 5, are {14, -4}
o Coming to the second equation, where |x + 9| = 25, which can be written as, |x - (9) | = 25, the two numbers that are 25 units away from -9 are -34 and 16, as we can see in the diagram below.
- Thus, the values of x, that satisfy the equation, |x + 9| = 25, are {-34, 16}
Therefore, the values of x, that satisfy the equation, ||x + 9| - 15| = 10, are {-34, -14, -4, 16}
Key Takeaways
- 1. In this question, we learnt how to solve an absolute value equation involving more than 1 modulus.
- a) And, to do that, we always start simplifying the equation from the outer most modulus and then we move to inner moduli.
2. We also learnt that substituting the inner moduli as a variable helps us to solve the question easily.
With these learnings in mind, let us now move to the next question.
e-GMAT Example 2
How many values of x, satisfy the equation ||2x - 7| - 3| = 12?
A. 0
B. 1
C. 2
D. 3
E. 4
Solution
Let's now use our learnings from previous question to solve an equation, which is pretty much similar to the previous equation except that the co-efficient of x is not equal to 1, in this question.
- o So, as we already know, first, let's substitute the inner modulus, |2x - 7| as y
- o Hence, we get, |y - 3| = 12
Now, applying the logic, that is shown in the concept video, we can say that y is a number, which is at a distance of 12 units from point, "3" on the number line
o Let's represent 3 on a number line and find the values of y that are 12 units away from "3"
So, from the above diagram, we can see that the two possible values of y are {-9, 15}
o Substituting back the modulus in the above equation, we get 2 equations,
- o |2x - 7| = -9, or
o |2x - 7| = 15
Now, we need to solve each of the above two equations to find all the possible values of x.
o So, let's consider the first equation, |2x - 7| = -9. If we observe this equation carefully, we can say that this equation has no solution, since, the value of a modulus cannot be negative.
o Thus, we do not have to solve this equation. We can simply say that there is no value of x, which satisfies this equation.
Trap:
If you fail to notice this, you end up marking the answer as E, thinking, since, there are 2 moduli, we would be getting 4 values of x as seen in the previous question. But, then you will fall in the trap that the question maker has set for you.
So, we should always keep in mind the basic definition of absolute value while solving an equation.
o Now, considering the second equation, |2x - 7| = 15, we can solve this as the modulus value is greater than zero.
o So, as shown in the concept video, first we need to divide the equation by 2, on both sides, to make the coefficient of x as 1
- o Dividing by 2, we get, |x - 3.5| = 7.5
o Now that, we have the equation in its general form, we can say that x is a number, which is at a distance of 7.5 units from the point "3.5"
o Representing this on a number line as shown below, we get the values of x as {-4, 11}
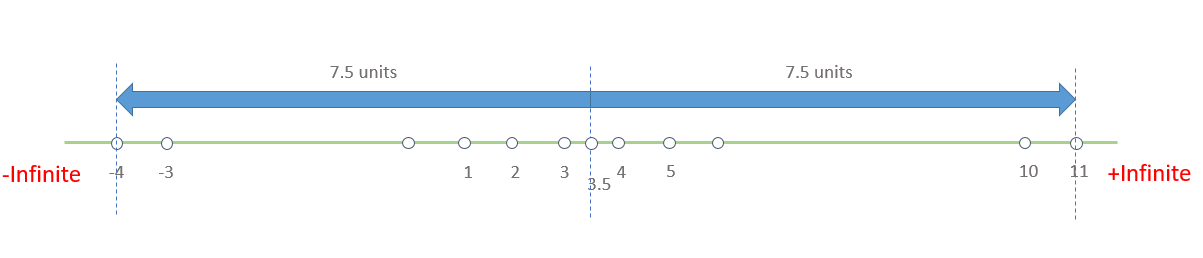
o Therefore, the number of possible values of x that satisfies the given equation, ||2x - 7|-3| = 12, is 2
Hence the correct answer is Option C.
Key Takeaways
- 1. In this question, we learnt how to solve an absolute value equation in which the coefficient of x is not equal to 1.
- a) To solve such equation, we need to divide the entire equation by the coefficient of x.
Next Topic - Absolute Inequalities
Now that you have mastered the concept of Absolute Equations, you have won half the battle in tackling Absolute value questions. Now, it's time to master the concept of Absolute Inequalities to win the other half.
- o Click here to get started with the concept of Absolute Inequalities now.
Get amazing free resources
e-GMAT offers a variety of free video lessons (25+) and diagnostic quizzes (400+ questions) on different topics. Start your free trial and learn using our immersive course.
- o Click here to sign up to our comprehensive free trial
We suggest that you follow the sequence mentioned below:
- 1. Get started by going through the video lessons embedded above to learn the basics.
2. Then go through the following questions in this article to learn how to solve Absolute Equation questions that involve multiple modulus.
3. Finally go through the concept of Absolute Inequalities, to continue learning.
e-GMAT Example 1
If x is an integer, then find the values of x that satisfy the equation ||x + 9| - 15| = 10?
Solution
As we can see that we are given one modulus inside another modulus:
- o That is, |x+9| is inside ||x+9|-15|.
o And, we are asked to find out all the possible values of x such that ||x + 9| - 15| = 10.
So, how do we solve this question?
- o Well, we will simply apply the basic properties of absolute values.
- 1. We will first solve the outermost modulus.
- a. And, while solving it, we can substitute the inner modulus with an appropriate variable such as y.
3. Now, this process will continue even if we had more than 2 moduli in the question.
- a. We will first solve the outermost and then we move from outermost modulus to the inner moduli.
So, let's apply the same process here.
- o We will start from the outer modulus.
- o Therefore, let us substitute the inner modulus, |x+9|= y.
- Hence, we get |y - 15| = 10.
o Now, let's focus our energy on solving the equation |y - 15| = 10
- From the concept video, we learnt that the form |x - a| = b represents numbers on the number line that are at a distance of 'b' units from 'a'
Applying this logic, to the equation |y - 15| = 10, we can say that y is a number at a distance of 10 units from "15".
o So, let's find out all the numbers, which are at a distance of 10 units from the point '15', by representing it on a number line.
- o If we observe the diagram above, we can notice that there can be two possible numbers, which are at a distance of 10 units from 15.
- One on the left side of 15, which is 10 units away from it = 15 - 10 = 5 and
One on the right side of 15, which is 10 units away from it = 15 + 10 = 25
o Hence, the possible values of y are 5 and 25
o Substituting back the modulus in the above equation, we get,
- |x + 9| = 5, or
|x + 9| = 25
o Let's solve each modulus individually and find the values of x
o Considering the first case, where |x + 9| = 5, we need to find the values of x, which are at a distance of 5 units from -9.
- Now, most of you might wonder, why did we consider -9, instead of 9. But, if we observe the general equation of modulus carefully, it is of the form |x - a| = b., where x is b units away from point 'a'.
And, in this case, we can write |x + 9| = 5 as |x - (-9) | = 5.
Note: So, remember to notice the sign of 'a' carefully as it is a common mistake done by users and you would find one of the answer choices to set you up in this trap.
So, representing -9 on a number line, we can find that the numbers, which are at a distance of 5 units from -9 are -14 and -4
- Thus, the values of x that satisfy the equation, |x + 9| = 5, are {14, -4}
o Coming to the second equation, where |x + 9| = 25, which can be written as, |x - (9) | = 25, the two numbers that are 25 units away from -9 are -34 and 16, as we can see in the diagram below.
- Thus, the values of x, that satisfy the equation, |x + 9| = 25, are {-34, 16}
Therefore, the values of x, that satisfy the equation, ||x + 9| - 15| = 10, are {-34, -14, -4, 16}
Key Takeaways
- 1. In this question, we learnt how to solve an absolute value equation involving more than 1 modulus.
- a) And, to do that, we always start simplifying the equation from the outer most modulus and then we move to inner moduli.
2. We also learnt that substituting the inner moduli as a variable helps us to solve the question easily.
With these learnings in mind, let us now move to the next question.
e-GMAT Example 2
How many values of x, satisfy the equation ||2x - 7| - 3| = 12?
A. 0
B. 1
C. 2
D. 3
E. 4
Solution
Let's now use our learnings from previous question to solve an equation, which is pretty much similar to the previous equation except that the co-efficient of x is not equal to 1, in this question.
- o So, as we already know, first, let's substitute the inner modulus, |2x - 7| as y
- o Hence, we get, |y - 3| = 12
Now, applying the logic, that is shown in the concept video, we can say that y is a number, which is at a distance of 12 units from point, "3" on the number line
o Let's represent 3 on a number line and find the values of y that are 12 units away from "3"
So, from the above diagram, we can see that the two possible values of y are {-9, 15}
o Substituting back the modulus in the above equation, we get 2 equations,
- o |2x - 7| = -9, or
o |2x - 7| = 15
Now, we need to solve each of the above two equations to find all the possible values of x.
o So, let's consider the first equation, |2x - 7| = -9. If we observe this equation carefully, we can say that this equation has no solution, since, the value of a modulus cannot be negative.
o Thus, we do not have to solve this equation. We can simply say that there is no value of x, which satisfies this equation.
Trap:
If you fail to notice this, you end up marking the answer as E, thinking, since, there are 2 moduli, we would be getting 4 values of x as seen in the previous question. But, then you will fall in the trap that the question maker has set for you.
So, we should always keep in mind the basic definition of absolute value while solving an equation.
o Now, considering the second equation, |2x - 7| = 15, we can solve this as the modulus value is greater than zero.
o So, as shown in the concept video, first we need to divide the equation by 2, on both sides, to make the coefficient of x as 1
- o Dividing by 2, we get, |x - 3.5| = 7.5
o Now that, we have the equation in its general form, we can say that x is a number, which is at a distance of 7.5 units from the point "3.5"
o Representing this on a number line as shown below, we get the values of x as {-4, 11}
o Therefore, the number of possible values of x that satisfies the given equation, ||2x - 7|-3| = 12, is 2
Hence the correct answer is Option C.
Key Takeaways
- 1. In this question, we learnt how to solve an absolute value equation in which the coefficient of x is not equal to 1.
- a) To solve such equation, we need to divide the entire equation by the coefficient of x.
Next Topic - Absolute Inequalities
Now that you have mastered the concept of Absolute Equations, you have won half the battle in tackling Absolute value questions. Now, it's time to master the concept of Absolute Inequalities to win the other half.
- o Click here to get started with the concept of Absolute Inequalities now.
Get amazing free resources
e-GMAT offers a variety of free video lessons (25+) and diagnostic quizzes (400+ questions) on different topics. Start your free trial and learn using our immersive course.
- o Click here to sign up to our comprehensive free trial
11 Jul 2019, 09:56
Kudos
Bookmarks
Thanks ...it is very helpful.
17 Jun 2025, 12:19
Kudos
Bookmarks
Automated notice from GMAT Club BumpBot:
A member just gave Kudos to this thread, showing it’s still useful. I’ve bumped it to the top so more people can benefit. Feel free to add your own questions or solutions.
This post was generated automatically.
A member just gave Kudos to this thread, showing it’s still useful. I’ve bumped it to the top so more people can benefit. Feel free to add your own questions or solutions.
This post was generated automatically.
