GMAT Changed on April 16th - Read about the latest changes here
close

It is currently 27 May 2018, 08:27
Search
Register
GMAT Club Tests
Decision Tracker
My Rewards
New posts
Unanswered

Close

GMAT Club Daily Prep

Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.

Customized
for You

we will pick new questions that match your level based on your Timer History

Track
Your Progress

every week, we’ll send you an estimated GMAT score based on your performance

Practice
Pays

we will pick new questions that match your level based on your Timer History

Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.

Go to My Workbook Learn more
Close

Request Expert Reply

Confirm Cancel

Events & Promotions

Events & Promotions in June
Open Detailed Calendar
CLICK HERE TO HIDE/SHOW EVENTS

Beauty of Coordinate geometry

  new topic post reply Question banks Downloads My Bookmarks Reviews Important topics  
  Sort by Date Sort by Kudos  
Search for:
 
Print view
First unread post
Author Message
TAGS:

Hide Tags
10 KUDOS received
Retired Moderator
User avatar
S
Joined: 18 Sep 2014
Posts: 1175
Location: India
GMAT ToolKit User Premium Member Reviews Badge
Beauty of Coordinate geometry [#permalink]

Show Tags

New post 24 Feb 2016, 10:42
10
This post received
KUDOS
15
This post was
BOOKMARKED

Coordinate geometry



Mathematics is a wonderful subject where you can solve one problem in numerous ways.
Coordinate geometry simplifies the Geometry much further and makes it easy.

Here is a problem from Veritas question bank simple but wonderful to test various concepts.

Attachment:
Geometry_Img48.png
Geometry_Img48.png [ 7.7 KiB | Viewed 5351 times ]

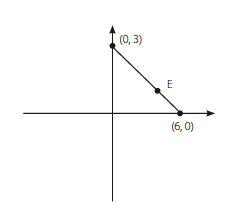
If the x-coordinate of point E is 4, what is its y-coordinate?

    A. \(\frac{-1}{2}\)
    B. \(1\)
    C. \(\frac{3}{2}\)
    D. \(2\)
    E. \(\frac{7}{2}\)



Different Methods to solve the above problem

Let me consider

\(A (0,3)\)
\(B (6,0)\)
\(E (4,y)\)
Origin \(O(0,0)\)
Lets drop a perpendicular from E to X axis at \((4,0)\) and say it \(F.\)




1. Traditional distance method



Distance between any two points \((x_1,y_1)\) and \((x_2,y_2)\) in coordination plane is

\(\sqrt{(y_2-y_1)^2+(x_2-x_1)^2}\)

\(AE+EB=AB\)

\(\sqrt{4^2+(y-3)^2}\)+\(\sqrt{y^2+2^2}\)=\(\sqrt{6^2+3^2}\)

subtract \(\sqrt{y^2+2^2}\) on both sides

\(\sqrt{y^2-6y+25}\)=\(\sqrt{45}\)-\(\sqrt{y^2+4}\)

squaring on both sides

\(y^2-6y+25=45+y^2+4-2\sqrt{45}\sqrt{y^2+4}\)

After cancelling similar terms like y^2 and simplifying the terms, Equation looks like

\(3y+12=\sqrt{45*(y^2+4)}\)

squaring on both sides again, we get

\(9(y^2+16+8y)=45(y^2+4)\)

on bringing all terms to one side and simplification, we get \((y-1)^2=0\)

i.e., \(y=1\)

This method is quite time consuming and cumbersome.




2. Form an equation and Substitute the value



Two Intercept Form for the Equation of a Line

\(\frac{x}{a}+\frac{y}{b}=1\), where a is the x-intercept and b is the y-intercept.

with points A and B, make an equation for line AB

\(\frac{x}{6}+\frac{y}{3}=1\)

Since point E lies on line AB, substitute \(E(4,y)\) in above equation

\(\frac{4}{6}+\frac{y}{3}=1\)

solving for y, we get \(y=1\)


Equation of line can also be formed with two points A(x1,y1), B(x2,y2) and slope of line AB m.
It can be represented as

\(m=\frac{(y_2-y_1)}{(x_2-x_1)}\)

equation of line is \(y-y_1=m(x-x_1)\) or \(y-y_2=m(x-x_2)\)

now we get \(y=1\) as we substitute \(E(4,y)\) as above.




3. Midpoint method



Midpoint between (0,3) and (6,0) is (3, (3/2) = (3, 1.5).

Because point E is below the midpoint with an x-coordinate of 4 and the y-coordinate had to be less than 1.5.
The only answer choice below 1.5 yet above 0 is 1 as in option B.




4. Slope method



Equate the slope of Line AE and EB since both the lines Coincide.

\(\frac{(y-3)}{(4-0)}=\frac{(0-y)}{(6-4)}\)

we get solve for y now.




5. Trigonometry



GMAT doesnt require you to know trigonometric functions and values of 0, 30,45,60,90 degree angles but it is always good to know
Those who are not aware of trigonometry, please refer to overview section of below link.
https://en.wikipedia.org/wiki/Trigonometry

Now Lets drop a perpendicular from E to X axis at (4,0) and say it F. It appears as in fig.
Attachment:
New Doc 5_1.jpg
New Doc 5_1.jpg [ 18.68 KiB | Viewed 5306 times ]


\(tan∠ABO=tan∠EBF\)

\(tan(θ)\)=opposite side/adjacent side

In OAB, \(tan∠ABO=\frac{OA}{OB}\)
In EBF, \(tan∠EBF=\frac{EF}{FB}\)

\(\frac{OA}{OB}\)=\(\frac{EF}{FB}\)

i.e., \(\frac{3}{6}\)=\(\frac{y}{(6-4)}\)

now we can solve for y.




6. Similar triangles



OAB and EFB are similar triangles for EF is parallel to OA.

Triangle Proportionality Theorem.
If a line parallel to one side of a triangle intersects the other two sides of the triangle, then the line divides these two sides proportionally.

\(\frac{BE}{BA}=\frac{BF}{BO}\)=\(\frac{EF}{OA}\)

to solve in simple terms, we take

\(\frac{BF}{BO}\)=\(\frac{EF}{OA}\)

\(\frac{2}{6}=\frac{y}{3}\) and hence \(y=1\).


:) Mathematics may not teach us how to add love or how to minus hate. But it gives every reason to hope that every problem has not one but multiple solutions. :)
SVP
SVP
avatar
P
Joined: 12 Dec 2016
Posts: 1905
Location: United States
Schools: Stanford '19, LBS '19, Carroll '19
GMAT 1: 700 Q49 V33
GPA: 3.64
GMAT ToolKit User Premium Member
Re: Beauty of Coordinate geometry [#permalink]

Show Tags

New post 15 Jul 2017, 02:48
I have a question, how useful each method is in solving a gmat question?
It is because these methods seem to prove your creativity rather than gmat skills.
Intern
Intern
avatar
Joined: 09 Nov 2016
Posts: 5
Location: India
Concentration: Marketing, General Management
GPA: 3.6
Re: Beauty of Coordinate geometry [#permalink]

Show Tags

New post 16 Dec 2017, 11:06
I tried finding the slope of line AB by y2-y1/x2-x1 and then formed an equation which came out to be y=-1/2x+3/2 and then substitute x=4 and y=y in the above equation. Got -7/2 as the answer. Can anyone please shed what's wrong with my approach?
1 KUDOS received
SVP
SVP
avatar
P
Joined: 12 Dec 2016
Posts: 1905
Location: United States
Schools: Stanford '19, LBS '19, Carroll '19
GMAT 1: 700 Q49 V33
GPA: 3.64
GMAT ToolKit User Premium Member
Re: Beauty of Coordinate geometry [#permalink]

Show Tags

New post 16 Dec 2017, 12:03
1
This post received
KUDOS
chavantusharr wrote:
I tried finding the slope of line AB by y2-y1/x2-x1 and then formed an equation which came out to be y=-1/2x+3/2 and then substitute x=4 and y=y in the above equation. Got -7/2 as the answer. Can anyone please shed what's wrong with my approach?


I think the line AB intersects the y-axis at (0,3) => y = (-1/2)x + 3
Intern
Intern
avatar
Joined: 09 Nov 2016
Posts: 5
Location: India
Concentration: Marketing, General Management
GPA: 3.6
Re: Beauty of Coordinate geometry [#permalink]

Show Tags

New post 17 Dec 2017, 09:01
I just made a very silly mistake. Thankyou chesstitans
Re: Beauty of Coordinate geometry   [#permalink] 17 Dec 2017, 09:01
Print view
First unread post
Display posts from previous: Sort by

Beauty of Coordinate geometry

  new topic post reply Question banks Downloads My Bookmarks Reviews Important topics  

Moderators: chetan2u, VeritasPrepKarishma, niks18, Bunuel, mikemcgarry

Search for:


GMAT Club MBA Forum Home| About| Terms and Conditions and Privacy Policy| GMAT Club Rules| Contact| Sitemap

Powered by phpBB © phpBB Group | Emoji artwork provided by EmojiOne

Kindly note that the GMAT® test is a registered trademark of the Graduate Management Admission Council®, and this site has neither been reviewed nor endorsed by GMAC®.

Main navigation

GMAT Resources

Partners

MBA Resources

www.gmac.com|www.mba.com | | GMAT Club Rules | Terms and Conditions