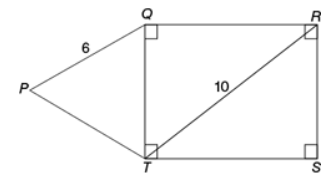
In the figure above, what is the area of region PQRST ? (1) PQ = RS (

The Logical approach to this question will the observation that the area we're looking for is of a shape which doesn't have a matching formula. Thus, we should either refer to it as the sum of or the difference between two familiar shapes. In this case, the sum of a rectangle and a triangle.
Statement (1) tells us that the sides of the rectangle are 6, which is enough to find the other side of the rectangle (using the pythagorean triplet 6,8,10). However, we don't have a height required to find the area of the triangle. Thus, answers (A) and (D) are eliminated.
Statement (2): Knowing that the triangle is an isosceles triangle is not enough to find its area. Answer choice (B) is eliminated.
Combining both statements, we now know that the triangle is an equilateral triangle, so the length of one side is enough to find its area.
The correct answer is (C).

Posted from my mobile device

Target question: What is the area of region PQRST ?

Statement 1: PQ = RS

IMPORTANT: For geometry Data Sufficiency questions, we are typically checking to see whether the statements "lock" a particular angle, length, or shape into having just one possible measurement. This concept is discussed in much greater detail in the video below.

This technique can save a lot of time.

Now that we know PQ = RS, we know that RS = 6
Since the diagonal RT = 10, we can apply the Pythagorean Theorem to see that QR = 8, which means rectangle QRST has area 48
HOWEVER, we don't yet know the area of triangle PQT. Here's why:
Notice that no given information LOCKS IN the position of side PQ.
If we think of side PQ as a door with its hinge at point Q, then side PQ can freely move around, changing the area of triangle PQT
Since triangle PQT can have a variety of angles, we cannot determine the area of region PQRST
Since we cannot answer the target question with certainty, statement 1 is NOT SUFFICIENT

Statement 2: PT = QT
Since we aren't provided any information about the lengths of PT and QT, we cannot determine the area of region PQRST
Since we cannot answer the target question with certainty, statement 2 is NOT SUFFICIENT

Statements 1 and 2 combined
Statement 1 tells us that rectangle QRST has area 48
From statement 1, we also see that side QT = 6

Statement 2 tells us that PT = QT = 6
So, triangle PQT is an EQUILATERAL with sides of length 6.
So, we now have enough information to find the area of PQRST.
Since we can answer the target question with certainty, the combined statements are SUFFICIENT

Answer: C

Cheers,
Brent

RELATED VIDEO

_________________

Please explain why statement 2 is insufficient:
Since we know the isosceles triangle. Side QT = RS, and Side QR can be found using Pythagorean theorem. Hence, it can be found. Thanks.

Hey Valhalla,

Knowing that QT= RS is insufficient to know their length. (In particular, it is also insufficient to calculate QR)
Try it!
Draw PT of length 6, build an isosceles triangle on top of it and build the square QRST off the side of that.
See how changing the lengths of the sides of the isosceles means that you will change the size of the square (because the diagonal must equal 10).
Then this is insufficient.

Thanks. I have mistakenly taken PT = QT = 6, that is why I could not fathom how statement 2 alone is insufficient. Dear David, thanks for replying. Any pointers you would give to avoid such mistakes? Thanks.

Hey Valhalla,

The mistake you describe is what we classify as a 'silly mistake'.
In other words, it is not that you didn't know the material, but rather that you missed / misinterpreted a small piece of data and therefore got the rest of the question wrong.
Tip number 1: Take a few seconds after reading the question but before diving into calculations to make sure you've copied everything down / read everything correctly. This is the best way to avoid such mistakes.
Tip number 2: Build up a timing strategy which doesn't leave you feeling completely rushed. It is better to guess a few questions and have enough time to do the others properly than to do everything in a hurried manner.
Tip number 3: Practice! The more questions you solve, the more familiar with the GMAT you get, and consequently the better you are able to notice the 'important' and 'tricky' details.

Best of luck,
David

Why is statement 1 insufficient?
We have diagonal as 10 and PQ=RS=6
So, we can find ST = 8
Since its a rectangle, we can directly find the area of this figure.
Similarly, for the triangle, we can take height which is divides QT in half and so by pythagoras, we can find the height of triangle as 5.

What have I considered wrong here?

Hey abannore,

You're right about the rectangle but wrong about the triangle.
The height only divides QT in half if the triangle is isosceles (if PQ = PT).
One way to SEE that there are many options is to imagine different angles for PQT.
If angle PQT were exactly 90 degrees, then PQ itself would be the height!
Instead, if angle PQT was very close to 0 then the triangle would be very 'narrow', and the height would also be very close to 0.
Two different options --> insufficient.

Best,
David

Hi All,

We're asked for the area of region PQRST. This question is based around a couple of Geometry rules. To properly find the area, we can break this shape into 2 pieces (a rectangle and a triangle), so we need to know the dimensions of the rectangle and the exact type of triangle - since we have one of the sides, we either need the 3 angles or the 2 missing sides - to calculate the overall area.

(1) PQ = RS

With the information in Fact 1, we know that the width of the rectangle is 6 and one of the two missing triangle sides is also 6. Along with the diagonal of the rectangle, we can now calculate its length (it's 8, since we have a 6/8/10 right triangle in the rectangle) but without the 3rd side of the triangle (or its 3 angles), we cannot calculate that other area.
Fact 1 is INSUFFICIENT

(2) PT = QT

The information in Fact 2 tells us that the triangle is either Isosceles or Equilateral, but we still do not know enough to determine its area and we don't know the length or width of the rectangle, so we cannot determine its area either.
Fact 2 is INSUFFICIENT

Combined, we know...
PQ = RS
PT = QT

With both Facts, we know that the triangle's sides are 6/6/6, so it's Equilateral and we can calculate its area. We also know the area of the rectangle (it's 6x8 = 48), so we CAN determine the area of PQRST.
Combined, SUFFICIENT

Final Answer:

GMAT assassins aren't born, they're made,
Rich
_________________

Hi everyone.

I have a “silly ques”- why cant this alleged rectangle be a square? What property am I missing?

TIA

Sambhav

Posted from my mobile device

Hi Sambhav,

In my explanation (which is right above yours), I work through that the information in Fact 1 proves that the rectangle is a 6x8 (and not a square). I didn't go through that extra work in Fact 2 because it wasn't necessary - BUT the information in Fact 2 does not restrict the rectangle to a 6x8. With Fact 2, we could actually be dealing with a square (if the sides were 5√2, then we would have a square and an isosceles triangle (with a different total area than if we had a 6x8 rectangle and triangle).

GMAT assassins aren't born, they're made,
Rich
_________________

Hello All,

How can we came to conclusion that QRST is rectangle? Does four angles =90 degree is sufficient condition for a figure to be
rectangle? As we don't have any information that opposite sides are equal or parallel

Thanks

Hi anand.prakash90,

Yes - when dealing with a 4-sided shape, if all four angles are 90-degree angles, then the sides ARE parallel and the shape IS a rectangle (and might actually be a square, which is ultimately a specific type of rectangle).

GMAT assassins aren't born, they're made,
Rich
_________________

Hi Genoa2000,

If you know any one of the sides in a 30/60/90 or 45/45/90 right triangle, then you can figure out all of the other sides (and then the area, perimeter, etc.). The reason why is because there are math 'relationships' between angles and the lengths of the sides that are across from those angles.

With those two types of triangles, we know already know the relationships (and you probably already have them memorized): 30/60/90 = X/X√3/2X and 45/45/90 = Y/Y/Y√2

For example, if a side length of 6 is across from the 30 degree angle in a 30/60/90, then we know that the 3 sides are 6/6√3/12.

With other triangles, there are still relationships, but we would need Trigonometry to define those exact relationships - they ARE defined though (and in a DS question, if you know that there is only one answer to the given question, then you have a 'Sufficient' situation (regardless of whether you can actually do the math to define that answer or not).

GMAT assassins aren't born, they're made,
Rich
_________________

Solution:

Question Stem Analysis:

We need to determine the area of region PQRST. Notice that the area of the region is composed of triangle PQT and rectangle QRST.

Statement One Alone:

From statement one, we see that RS = 6. Since triangle RST is a right triangle with side RS = 6 and hypotenuse RT = 10, side ST = 8 (notice triangle RST is a 6-8-10 right triangle). Since RS and ST are also the sides of rectangle QRST, the area of rectangle QRST is 6 x 8 = 48. However, we can’t determine the area of triangle PQT, so we can’t determine the area of region PQRST. Statement one alone is not sufficient.

Statement Two Alone:

From statement two, we see that triangle PQT is at least an isosceles triangle and perhaps an equilateral triangle. However, since we don’t know which one it really is, we can’t determine its area. Statement two alone is not sufficient.

Statements One and Two Together:

With the two statements, we see that RS = QT and since RS = 6, QT = 6. Furthermore, PT = QT = PQ = 6. This makes triangle PQT an equilateral triangle. Since we know a side of the equilateral triangle, we can determine its area. Lastly, since we’ve already determined the area of rectangle QRST to be 48, we can determine the area of region PQRST. Both statements together are sufficient.

Answer: C

_________________

Answer: Option C

Video solution by GMATinsight



Get TOPICWISE: Concept Videos | Practice Qns 100+ | Official Qns 50+ | 100% Video solution CLICK HERE.
Two MUST join YouTube channels : GMATinsight (1000+ FREE Videos) and GMATclub
_________________

I do not understand how statement two is not sufficient. We have square with a diagonal that equals 10. Diagonal inside a square is equal to S√ 2, Where S is equal to the side of the square. 10=S√ 2. Divide by root. We now have a value for S. With this value, we know that QT is equal to the value of S because QT is a side of the square. Knowing that PT=QT gives us our final value. What am I missing?


ScottTargetTestPrep

Hi Nmerritt1995,

We're asked for the area of region PQRST. This question is based around a couple of Geometry rules. To properly find the area, we can break this shape into 2 pieces (a rectangle and a triangle), so we need to know the dimensions of the rectangle and the exact type of triangle - since we have one of the sides, we either need the 3 angles or the 2 missing sides - to calculate the overall area.

With Fact 2, we are told that PT = QT. This means that the triangle is either Isosceles or Equilateral, but we still do not know enough to determine its area and we don't know the length or width of the rectangle, so we cannot determine its area either. It might be a square, but it might also be a rectangle.
Fact 2 is INSUFFICIENT

It's not until we combine all of the information that we are given that we know for sure that the triangle is Equilateral and the rectangle is a 6 x 8.

GMAT assassins aren't born, they're made,
Rich
_________________

Hello All,

If the diagonal bisects the rectangle, why can't it create two 45-45-90 triangles, thus making QT and QR 5\sqrt{2} ? Please let me know what I am missing.

thanks!