Bunuel wrote:
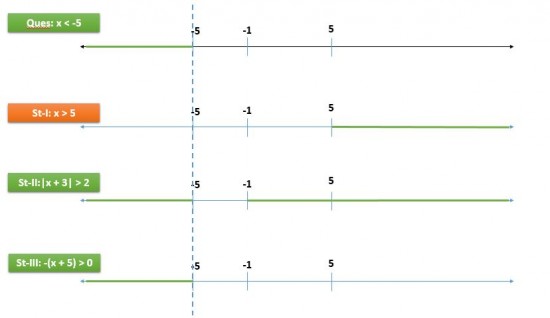
The Official Guide For GMAT® Quantitative Review, 2ND EditionIf 4<(7-x)/3, which of the following must be true?
I. 5<x
II. |x+3|>2
III. -(x+5) is positive
(A) II only
(B) III only
(C) I and II only
(D) II and III only
(E) I, II and III
First, let's deal with the given inequality.
4 < (7-x)/3
Multiply both sides by 3 to get: 12 < 7 - x
Add x to both sides: x + 12 < 7
Subtract 12 from both sides to get:
x < -5So, if
x < -5, which of the following statements MUST be true?
Aside: When dealing with "MUST be true" questions, we can eliminate a statement if we can find an instance where it is not true.I. 5 < x (MUST this be true?)
No!
If
x < -5, then it could be the case that x = -7, and -7 is NOT greater than 5
So, statement I need NOT be true.
II. |x+3| > 2 (MUST this be true?)
The answer is Yes. Here's why:
IMPORTANT CONCEPT:
|x - k| represents the DISTANCE between x and k on the number line. So, for example, we can think of |4 - 7| as the distance between 4 and 7 on the number line.
Notice that |4 - 7| = |-3| = 3, and 3 is indeed the distance between 4 and 7 on the number line.
Now let's examine |x+3|
We can rewrite this as |x - (-3)|
This represents the DISTANCE between x and -3 on the number line.
So, the inequality
|x-(-3)| > 2 is stating that the DISTANCE between x and -3 on the number line is GREATER THAN 2
Well, since we're told that
x < -5, we can be certain that the DISTANCE between x and -3 on the number line is
definitely GREATER THAN 2
[If you're not convinced, sketch a number line, and place a big dot at -3. Then choose ANY value for x such that x < -5. You'll see that the distance between x and -3 is greater than 2] So, statement II MUST be true.
III. -(x+5) is positive This is the same as saying
-(x+5) > 0 (MUST this be true?)
The answer is Yes. Here's why:
We're told that
x < -5If we add 5 to both sides we get x+5 < 0
Now, if we multiply both sides by -1, we get
-(x+5) > 0[aside: notice that, since I multiplied both sides by a negative value, I reversed the direction of the inequality] As we can see, statement III MUST be true.
Answer: D
Cheers,
Brent



 75%
(hard)
75%
(hard)
 48%
(02:01)
wrong
48%
(02:01)
wrong  based on 6125
sessions
based on 6125
sessions