UNSTOPPABLE12 wrote:
ScottTargetTestPrep wrote:
Bunuel wrote:
The Official Guide For GMAT® Quantitative Review, 2ND Edition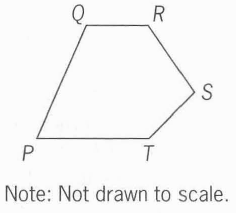
In pentagon PQRST, PQ= 3, QR = 2, RS = 4, and ST = 5. Which of the lengths 5, 10, and 15 could be the value of PT ?
(A) 5 only
(B) 15 only
(C) 5 and 10 only
(D) 10 and 15 only
(E) 5, 10, and 15
Problem Solving
Question: 150
Category: Geometry
Page: 82
Difficulty: 600
Solution:
This question can be answered by using the triangle inequality, which states that the length of the third side of a triangle is less than the sum of the lengths of the other two sides.
We can create 3 triangles in the pentagon: PQR, RST, and PRT.
For triangle PQR, two side lengths are 3 and 2, so the third side length (PR) must be less than 5.
For triangle RST, two side lengths are 4 and 5, so the third side length (RT) must be less than 9.
For triangle PRT, we know that the length of PR must be less than 5 and the length of RT must be less than 9. Thus, the length of the third side, PT, must be less than 14.
Of the possible lengths of PT, which are 5, 10, and 15, we see that only 5 and 10 meet the criteria of the triangle inequality.
Answer: C
Posted from my mobile deviceHello
ScottTargetTestPrep,
I was wondering whether you could clarify how did you find the minimum values, in your solution you mention that PT must be less than 14, but how do we know whether we could accept both 5 and 10, also you have mentioned that the length of PR must be less than 5 and the length of RT must be less than 9 so basically aren't we talking about 4+8=12 so shouldn't PT be less than 12?
We can actually use the triangle inequality to obtain lower bounds for the length of a side using the other two side lengths. If a, b and c are the side lengths of a triangle, then the triangle inequality tells us that c < a + b must be true. That's the upper bound. Now, let's use the triangle inequality for sides a and b:
a < b + c
c > a - b,
and
b < a + c
c> b - a
Notice that either a - b or b - a is non-negative and the above inequalities show that c must be longer than each of those differences. Thus, not only the length of a side must be shorter than the sum of the lengths of the remaining two sides, but also the length of a side must be longer than the positive difference between the lengths of the remaining sides.
Applying the above to the side PR, we see that 1 < PR < 5. So, PR can be anything between 1 and 5. Similarly, applying the same argument to side RT, we see that 1 < RT < 9. Finally, let's look at PT. We already know PT must be less than 14, but how short can PT be? Well, notice that 4 is a possible value for both PR and RT. If both PR and RT are 4, then PT must be longer than 4 - 4 = 0; i.e. PT can be made as short as we want (by choosing PR = RT and choosing the angle between PR and RT small enough).
To answer your second question, notice that it is not stated anywhere in the question that the distance between P and R is an integer. Similarly, the distance between R and T is not necessarily an integer either. If those distances were required to be integers, then indeed the maximum value of PR would be 4 and the maximum value of RT would be 8 and PT would have to be less than 4 + 8 = 12. However, as long as PR < 5 is satisfied, PR can be chosen as close to 5 as we want (for instance, we can choose PR to be 4.999). Similarly, RT can be chosen as close to 9 as we want (for instance, we can choose RT to be 8.999 or even closer). That is why PT can be greater than 12; in fact, PT can be made as close to 14 as we want by choosing PR and RT accordingly. However, PT can never equal 14 or anything greater than 14.



 45%
(medium)
45%
(medium)
 31%
(02:10)
wrong
31%
(02:10)
wrong  based on 4582
sessions
based on 4582
sessions












