In the figure above, segments RS and TU represent two positions of the

MUST KNOW FOR THE GMAT:
• A right triangle where the angles are 30°, 60°, and 90°.

This is one of the 'standard' triangles you should be able recognize on sight. A fact you should commit to memory is: The sides are always in the ratio \(1 : \sqrt{3}: 2\).
Notice that the smallest side (1) is opposite the smallest angle (30°), and the longest side (2) is opposite the largest angle (90°).

• A right triangle where the angles are 45°, 45°, and 90°.

This is one of the 'standard' triangles you should be able recognize on sight. A fact you should also commit to memory is: The sides are always in the ratio \(1 : 1 : \sqrt{2}\). With the \(\sqrt{2}\) being the hypotenuse (longest side). This can be derived from Pythagoras' Theorem. Because the base angles are the same (both 45°) the two legs are equal and so the triangle is also isosceles.

BACK TO THE ORIGINAL QUESTION:

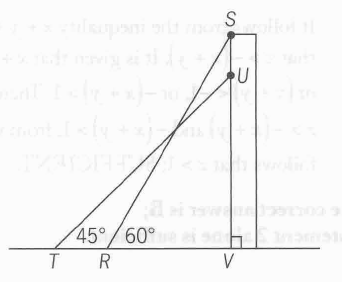In the figure above, segments RS and TU represent two positions of the same ladder leaning against the side SV of a wall. The length of TV is how much greater than Length of RV?

Given: RS=TU. Question: TV-RV=?

Now, according to the properties above if we knew RS (or which is the same TU), then we would be able to find ANY line segment in the given figure: RS would give us RV and SV, while TU would give us TV and UV. Thus knowing RS/TU would be sufficient to get the value of TV-RV.

If we knew RV: we could get RS (or which is the same TU) and would have the same exact case as above.

(1) The length of TU is 10 meters. Sufficient.
(2) The length of RV is 5 meters. Sufficient.

Answer: D.

Similar questions to practice:
a-ladder-25-feet-long-is-leaning-against-a-wall-that-is-130364.html
in-the-figure-above-segments-rs-and-tu-represent-two-140752.html
_________________

St1: The length of TU is 10 meters. Sufficient.

Triangle TUV is a 45-45-90 triangle. The sides are in the ratio of 1:1:root 2. We can calculate the length of TV. Since the stem mentions TU and RS are the same ladder, RS = 10. Now, triangle RSV is a 30-60-90 triangle. The sides are in the ratio of 1:root 3:2. We can calculate the length of RV.

St2: The length of RV is 5 meters. Sufficient. Applying same concept as statement 1, we can find TV.

Answer (D).

Option D.Each is sufficient.
Using basic trigo:
From S1: TU=RS=10 mts.
cos 45=TV/TU (cos 45=1/sqrt2 and TU=10)
We can find TV
And cos 60=RV/RS (cos 60=1/2 and RS=10
We can find RV
The diff can be found out.Sufficient.

From S2: RV=5
We can find RS and TU by the same trigo formula-cos (angle)=Base/Hypotenuse
Then the diff between TV and RV can be found out.Sufficient.

HI All,

This is a great "pattern matching" question, in that if you recognize what you're looking at, you won't need to do ANY math to get to the correct answer.

It doesn't take much to recognize the 30/60/90 and 45/45/90 right triangles in the drawing. The "key" to the shortcut is that we're told that that RS and TU are the SAME length - in math terms, this means that the hypotenuse of those two triangles is the SAME. By extension, if you know the length of ANY of the sides in EITHER of the triangles, then you can figure out EVERY side length in that drawing.

If you recognize this pattern, then dealing with the two Facts won't take much time or effort at all.

As an aside on the prior post in this thread, the GMAT will NEVER ask you a question that requires Trigonometry to solve it, so you do NOT need to know any Trig rules for this test.

GMAT assassins aren't born, they're made,
Rich

The most important point is here the word "THE SAME LADDER !!!" - missed it at the begining, but then could easily solve.. all other things in this question are just using known formulas for two particular triangles.

How have we determined that RS=TU? Bunuel

We are told that "RS and TU represent two positions of the SAME ladder", so line segments RS and TU are representing the SAME ladder just positioned in two different ways.

Hope it's clear.
_________________

"SAME LADDER" is the killer term here.

Bunuel VeritasKarishma

If "same" ladder was not mentioned, could we have still arrived at the same conclusion ?

If not, what would be the correct answer then ?

Please throw some light.

The same ladder means the hypotenuses are the same.
The two triangles are 45-45-90 and 30-60-90.
So for either triangle, if you know any one side's measure, you know the measure of all sides of that triangle.
Stmnt 1 gives one side of TUV so you know all sides of TUV. Since hypotenuse lengths are the same, you know all sides of RSV too and hence stmnt 1 alone is sufficient.
If the two hypotenuse were not equal, you would not know the length of sides of RSV.
Same logic applies to stmnt 2 too.

Hence, in that case, instead of (D), answer would be (C) since you would need both statements.
_________________

Hi avigutman -

If ABC is a non right angled triangle with fixed angles - 20 | 35 | 125 degree

1) You are given the length of one side (say 15 meters) -- are the lengths of the 2 other sides non-negiotiable ?

I think if ABC is a non right angled triangle instead with fixed angles - 35 | 55 | 90 degree

1) If you are given the length of one side (say 15 meters) -- the lengths of the 2 sides are non-negiotiable (i think)

jabhatta2 the three angles of a triangle fully determine the ratio of the three sides.
This is why triangles that have the same three angles are always similar shapes.
This is true regardless of whether one of the angles happens to be 90 degrees.

Thanks avigutman - i think what you are implying is if angle SVR was NOT 90 degrees in the original question -- one can select D as the answer without pen and paper ?

jabhatta2 In this hypothetical, is SVR known? If so, then yes.

Ans D
The key to the answer is to understand that SR and TU are 2 different positions of the same ladder and hence SR=TU

Hello from the GMAT Club BumpBot!

Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).

Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.
_________________