Bunuel wrote:
What is the area of the hexagonal region shown in the figure above?
(A) 54√3
(B) 108
(C) 108√3
(D) 216
(E) cannot be determined
Attachment:
 2017-09-20_1021_002ed.png [ 21.16 KiB | Viewed 11897 times ]
2017-09-20_1021_002ed.png [ 21.16 KiB | Viewed 11897 times ]
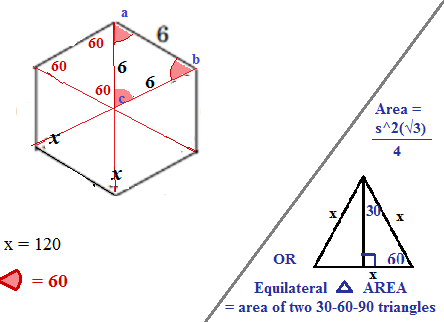
The hexagon can be divided into triangles. (
Ignore the right corner of the diagram if you know the formula for area of an equilateral triangle.)
This hexagon is regular: side lengths and angles are all equal.
1) Draw diagonals. A regular hexagon can be divided into six identical equilateral triangles*
2) Find the area of one equilateral triangle and multiply by 6 to get total area of hexagon
Area of equilateral triangle** with side = s (side here = 6) is
\(\frac{s^2\sqrt{3}}{4}\)
\(\frac{6^2\sqrt{3}}{4}\)
\(\frac{36\sqrt{3}}{4}\) = \(9\sqrt{3}\)
\((9\sqrt{3}) * 6\) =
\(54√3\)
ANSWER A*
Regular hexagon can be divided into six identical equilateral trianglesEach angle measure is 120 degrees
The sum of interior angles of n-sided polygon, where n is the number of sides, is (n-2)* 180
(4 * 180) = 720 degrees total for all interior angles
There are six interior angles
720/6 = 120 per angle
Diagonals bisect the 120 degree angles, so at each vertex there are two 60 degree angles (diagram:
a and b)
At the center, where the diagonals intersect, there are 6 angles whose sum is 360
The angle nearest the center of each identical triangle also equals 60: 360/6 = 60 degrees (diagram:
c)
Three 60 degree angles (
a, b, c ) = equilateral triangle, and there are six of them
**
If formula for equilateral triangle is not known, see lower right corner of diagramDerive area by dropping an altitude from a vertex
The altitude of an equilateral triangle
---is a perpendicular bisector of the opposite side
---and bisects the vertex opposite that side, so
There are two angles with measure 30 at the top vertex, two right angles where altitude meets base, and two angles with measure 60
Thus there are two 30: 60: 90 triangles with side ratios x: \(x\sqrt{3}: 2x\)
Calculate the area of one such triangle and multiply by two to get the area of one equilateral triangle (then multiply by 6 for the hexagonal area)



 15%
(low)
15%
(low)
 19%
(02:09)
wrong
19%
(02:09)
wrong  based on 103
sessions
based on 103
sessions

