AdmitJA wrote:
Attachment:
The attachment Capture.PNG is no longer available
In the figure above, SQRE is a square and AB = AC. Is the area of triangle ABC greater than the area of square SQRE?
(1) The length of RE is less than twice the length of BR.
(2) AS = AQ
To rephrase the question, it is helpful to see what connections exist between the triangle and the square and furthermore how it is possible to relate their areas. Draw a vertical line from point A straight down to the base of the triangle (and label the bottom point of this line Z). This new line, AZ (of length x), is the height of triangle ABC and has the same length as any side of the square. Label the diagram with the rest of the given information: AB = AC, implying that triangle ABC is isosceles and that angle B must equal angle C.
Attachment:
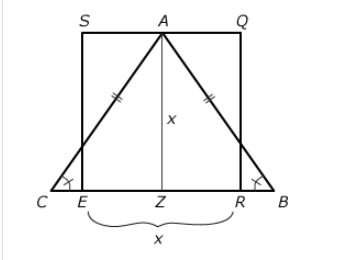 Capture.JPG [ 15.25 KiB | Viewed 17576 times ]
Capture.JPG [ 15.25 KiB | Viewed 17576 times ]
The area of the square can be expressed as \(x^2\) and the area of the triangle as \(1/2\)(BC)(x) (label all lengths equal to AZ as x)
Since BC is comprised of ER + RB + CE, and ER is also a side of the square or x, you can rewrite BC as
x + RB + CE. Thus the question becomes
“Is \(1/2\)(x+RB+CE)(x) > \(x^2\)?"If RB and CE together sum to the length of x, then the left side of the inequality will be identical to the right: \(1/2\)(x+x)(x) = \(x^2\)
For the left side of the inequality to be greater than the right, however, RB and CE must sum to more than x, thus the final rephrase can be stated as
“Is RB + CE > x?” (1) NOT SUFFICIENT: The statement can be translated as ER < 2RB
x < 2RB .... Again replacing ER with the variable x
\(x/2\) < RB
To know if RB + CE > x, you would need to know something about CE as well. Can you assume that CE = RB? From the given, triangle ABC is isosceles and thus symmetrical. However, there is no guarantee that is symmetrically placed in the square. If the triangle is symmetrically placed, RB = CE and both are greater than \(x/2\) and would thus sum to greater than x (scenario II below).
Scenario III below would also satisfy the question, but scenario I would not necessarily.
Attachment:
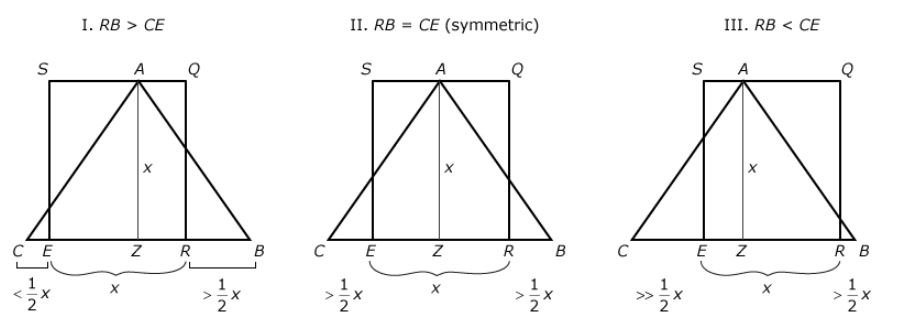 Capture1.JPG [ 34.93 KiB | Viewed 17595 times ]
Capture1.JPG [ 34.93 KiB | Viewed 17595 times ]
(2) NOT SUFFICIENT: This statement establishes the symmetric placement of triangle ABC within the square SQRE. On its own it does not relate RB and CE to x.
(1) AND (2) TOGETHER SUFFICIENT: Given the symmetric placement of triangle ABC within the square SQRE from statement (2) along with the information from statement (1), scenario II above is established and RB + CE > x.
The correct answer is (C).



 85%
(hard)
85%
(hard)
 48%
(02:37)
wrong
48%
(02:37)
wrong  based on 625
sessions
based on 625
sessions



