Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
3-D Geometries
This post is a part of [GMAT MATH BOOK]
created by: shrouded1
Scope
The GMAT often tests on the knowledge of the geometries of 3-D objects such cylinders, cones, cubes & spheres. The purpose of this document is to summarize some of the important ideas and formulae and act as a useful cheat sheet for such questions
Cube

cube.jpg [ 8.97 KiB | Viewed 57327 times ]
A cube is the 3-D generalisation of a square, and is characterized by the length of the side, \(a\). Important results include :
Cuboid
cuboid.jpg [ 16.29 KiB | Viewed 57441 times ]
A cuboid is the 3-D generalisation of a rectangle, and is characterized by the length of its sides, \(a,b,c\). Important results include :
Cylinder
cylinder.jpg [ 24.95 KiB | Viewed 57232 times ]
A cylinder is a 3-D object formed by rotating a rectangular sheet along one of its sides. It is characterized by the radius of the base, \(r\), and the height, \(h\). Important results include :
Cone
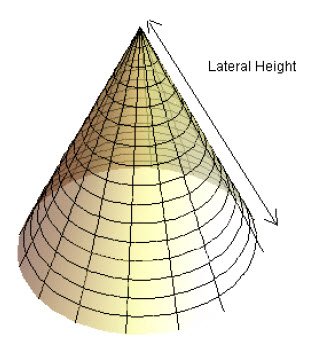
cone.jpg [ 31.94 KiB | Viewed 57071 times ]
A cone is a 3-D object obtained by rotating a right angled triangle around one of its sides. It is charcterized by the radius of its base, \(r\), and the height, \(h\). The hypotenuse of the triangle formed by the height and the radius (running along the diagnol side of the cone), is known as it lateral height, \(l=\sqrt{r^2+h^2}\). Important results include :
Sphere
sphere.jpg [ 32.94 KiB | Viewed 56926 times ]
A sphere is a 3-D generalisation of a circle. It is characterised by its radius, \(r\). Important results include :

hemisphere.jpg [ 36.64 KiB | Viewed 56843 times ]
A hemisphere is a sphere cut in half and is also characterised by its radius \(r\). Important results include :
Some simple configurations
These may appear in various forms on the GMAT, and are good practice to derive on one's own :
Examples
Example 1 : A certain right circular cylinder has a radius of 5 inches. There is oil filled in this cylinder to the height of 9 inches. If the oil is poured completely into a second right cylinder, then it will fill the second cylinder to a height of 4 inches. What is the radius of the second cylinder, in inches?
A. 6
B. 6.5
C. 7
D. 7.5
E. 8
Solution : The volume of the liquid is constant.
Initial volume = \(\pi * 5^2 * 9\)
New volume = \(\pi * r^2 * 4\)
\(\pi * 5^2 * 9 = \pi * r^2 * 4\)
\(r = (5*3)/2 = 7.5\)
Answer is (d)
Example 2 : A spherical balloon has a volume of 972 \(\pi\)cubic cm, what is the surface area of the balloon in sq cm?
A) 324
B) 729
C) 243 \(\pi\)
D) 324 \(\pi\)
E) 729 \(\pi\)
Solution : \(V=\frac{4}{3} \pi r^3\)
\(r = (\frac{3V}{4\pi})^{\frac{1}{3}} = (\frac{3 * 972 * \pi}{4 * \pi})^{\frac{1}{3}} = (3*243)^{1/3} = (3^6)^{1/3} = 9\)
\(A=4 \pi r^2 = 4 * \pi * 9^2=324 \pi\)
Answer (d)
Example 3 : A cube of side 5cm is painted on all its side. If it is sliced into 1 cubic centimer cubes, how many 1 cubic centimeter cubes will have exactly one of their sides painted?
A. 9
B. 61
C. 98
D. 54
E. 64
Solution : Notice that the new cubes will be each of side 1Cm. So on any face of the old cube there will be 5x5=25 of the smaller cubes. Of these, any smaller cube on the edge of the face will have 2 faces painted (one for every face shared with the bigger cube). The number of cubes that have exacly one face painted are all except the ones on the edges. Number on the edges are 16, so 9 per face.
There are 6 faces, hence 6*9=54 smaller cubes with just one face painted.
Answer is (d)
Example 4 : What is the surface area of the cuboid C ?
(1) The length of the diagnol of C is 5
(2) The sum of the sides of C is 10
Solution : Let the sides of cuboid C be \(x,y,z\)
We know that the surface area is given be \(2(xy+yz+zx)\)
(1) : Diagnol = \(\sqrt{x^2+y^2+z^2}=5\). Not sufficient to know the area
(2) : Sum of sides = \(x+y+z=10\). Not sufficient to know the area
(1+2) : Note the identity \((x+y+z)^2=x^2+y^2+z^2+2(xy+yz+zx)\)
Now we clearly have enough information.
\(2(xy+yz+zx) = 10^2 - 5^2 = 75\)
Sufficient
Answer is (c)
Some Other 3-D Problems
Sphere & Cube
Sphere & Cylinder
Cylinder & Cuboid
Cylinder & Cuboid II
Cylinder
Cube
Cube II
Cone
Cube III
Cylinder
Hemisphere
created by: shrouded1
Scope
The GMAT often tests on the knowledge of the geometries of 3-D objects such cylinders, cones, cubes & spheres. The purpose of this document is to summarize some of the important ideas and formulae and act as a useful cheat sheet for such questions
Cube
Attachment:
cube.jpg [ 8.97 KiB | Viewed 57327 times ]
A cube is the 3-D generalisation of a square, and is characterized by the length of the side, \(a\). Important results include :
- Volume = \(a^3\)
- Surface Area = \(6a^2\)
- Diagnol Length = \(\sqrt{3}a\)
Cuboid
Attachment:
cuboid.jpg [ 16.29 KiB | Viewed 57441 times ]
A cuboid is the 3-D generalisation of a rectangle, and is characterized by the length of its sides, \(a,b,c\). Important results include :
- Volume = \(abc\)
- Surface Area = \(2(ab+bc+ca)\)
- Diagnol Length = \(\sqrt{a^2+b^2+c^2}\)
Cylinder
Attachment:
cylinder.jpg [ 24.95 KiB | Viewed 57232 times ]
A cylinder is a 3-D object formed by rotating a rectangular sheet along one of its sides. It is characterized by the radius of the base, \(r\), and the height, \(h\). Important results include :
- Volume = \(\pi r^2 h\)
- Outer surface area w/o bases = \(2 \pi r h\)
- Outer surface area including bases = \(2 \pi r (r+h)\)
Cone
Attachment:
cone.jpg [ 31.94 KiB | Viewed 57071 times ]
A cone is a 3-D object obtained by rotating a right angled triangle around one of its sides. It is charcterized by the radius of its base, \(r\), and the height, \(h\). The hypotenuse of the triangle formed by the height and the radius (running along the diagnol side of the cone), is known as it lateral height, \(l=\sqrt{r^2+h^2}\). Important results include :
- Volume = \(\frac{1}{3} \pi r^2 h\)
- Outer surface area w/o base = \(\pi r l =\pi r \sqrt{r^2+h^2}\)
- Outer surface area including base = \(\pi r (r+l)=\pi r (r+\sqrt{r^2+h^2})\)
Sphere
Attachment:
sphere.jpg [ 32.94 KiB | Viewed 56926 times ]
A sphere is a 3-D generalisation of a circle. It is characterised by its radius, \(r\). Important results include :
- Volume = \(\frac{4}{3} \pi r^3\)
- Surface Area= \(4 \pi r^2\)
Attachment:
hemisphere.jpg [ 36.64 KiB | Viewed 56843 times ]
A hemisphere is a sphere cut in half and is also characterised by its radius \(r\). Important results include :
- Volume = \(\frac{2}{3} \pi r^3\)
- Surface Area w/o base = \(2 \pi r^2\)
- Surface Area with base = \(3 \pi r^2\)
Some simple configurations
These may appear in various forms on the GMAT, and are good practice to derive on one's own :
- Sphere inscribed in cube of side \(a\) : Radius of sphere is \(\frac{a}{2}\)
- Cube inscribed in sphere of radius \(r\) : Side of cube is \(\frac{2r}{\sqrt{3}}\)
- Cylinder inscribed in cube of side \(a\) : Radius of cylinder is \(\frac{a}{2}\); Height \(a\)
- Cone inscribed in cube of side \(a\) : Radius of cone is \(\frac{a}{2}\); Height \(a\)
- Cylinder of radius \(r\) in sphere of radius \(R\) (\(R>r\)) : Height of cylinder is \(2\sqrt{R^2-r^2}\)
Examples
Example 1 : A certain right circular cylinder has a radius of 5 inches. There is oil filled in this cylinder to the height of 9 inches. If the oil is poured completely into a second right cylinder, then it will fill the second cylinder to a height of 4 inches. What is the radius of the second cylinder, in inches?
A. 6
B. 6.5
C. 7
D. 7.5
E. 8
Solution : The volume of the liquid is constant.
Initial volume = \(\pi * 5^2 * 9\)
New volume = \(\pi * r^2 * 4\)
\(\pi * 5^2 * 9 = \pi * r^2 * 4\)
\(r = (5*3)/2 = 7.5\)
Answer is (d)
Example 2 : A spherical balloon has a volume of 972 \(\pi\)cubic cm, what is the surface area of the balloon in sq cm?
A) 324
B) 729
C) 243 \(\pi\)
D) 324 \(\pi\)
E) 729 \(\pi\)
Solution : \(V=\frac{4}{3} \pi r^3\)
\(r = (\frac{3V}{4\pi})^{\frac{1}{3}} = (\frac{3 * 972 * \pi}{4 * \pi})^{\frac{1}{3}} = (3*243)^{1/3} = (3^6)^{1/3} = 9\)
\(A=4 \pi r^2 = 4 * \pi * 9^2=324 \pi\)
Answer (d)
Example 3 : A cube of side 5cm is painted on all its side. If it is sliced into 1 cubic centimer cubes, how many 1 cubic centimeter cubes will have exactly one of their sides painted?
A. 9
B. 61
C. 98
D. 54
E. 64
Solution : Notice that the new cubes will be each of side 1Cm. So on any face of the old cube there will be 5x5=25 of the smaller cubes. Of these, any smaller cube on the edge of the face will have 2 faces painted (one for every face shared with the bigger cube). The number of cubes that have exacly one face painted are all except the ones on the edges. Number on the edges are 16, so 9 per face.
There are 6 faces, hence 6*9=54 smaller cubes with just one face painted.
Answer is (d)
Example 4 : What is the surface area of the cuboid C ?
(1) The length of the diagnol of C is 5
(2) The sum of the sides of C is 10
Solution : Let the sides of cuboid C be \(x,y,z\)
We know that the surface area is given be \(2(xy+yz+zx)\)
(1) : Diagnol = \(\sqrt{x^2+y^2+z^2}=5\). Not sufficient to know the area
(2) : Sum of sides = \(x+y+z=10\). Not sufficient to know the area
(1+2) : Note the identity \((x+y+z)^2=x^2+y^2+z^2+2(xy+yz+zx)\)
Now we clearly have enough information.
\(2(xy+yz+zx) = 10^2 - 5^2 = 75\)
Sufficient
Answer is (c)
3-D Geometry Questions:
https://gmatclub.com/forum/geometry-3-d ... 75006.htmlSome Other 3-D Problems
Sphere & Cube
Sphere & Cylinder
Cylinder & Cuboid
Cylinder & Cuboid II
Cylinder
Cube
Cube II
Cone
Cube III
Cylinder
Hemisphere










