Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
ABSOLUTE VALUE
(Modulus)
This post is a part of [GMAT MATH BOOK]
created by: walker
edited by: bb, Bunuel
Definition
The absolute value (or modulus) \(|x|\) of a real number x is x's numerical value without regard to its sign.
For example, \(|3| = 3\); \(|-12| = 12\); \(|-1.3|=1.3\)
Graph:
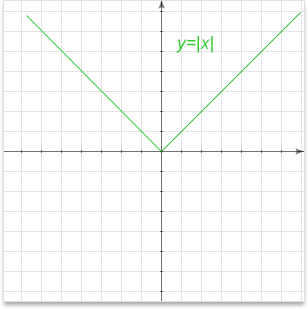
Important properties:
\(|x|\geq0\)
\(|0|=0\)
\(|-x|=|x|\)
\(|x|+|y|\geq|x+y|\)
How to approach equations with moduli
It's not easy to manipulate with moduli in equations. There are two basic approaches that will help you out. Both of them are based on two ways of representing modulus as an algebraic expression.
1) \(|x| = \sqrt{x^2}\). This approach might be helpful if an equation has × and /.
2) |x| equals x if x>=0 or -x if x<0. It looks a bit complicated but it's very powerful in dealing with moduli and the most popular approach too (see below).
3-steps approach:
General approach to solving equalities and inequalities with absolute value:
1. Open modulus and set conditions.
To solve/open a modulus, you need to consider 2 situations to find all roots:
For example, \(|x-1|=4\)
a) Positive: if \((x-1)\geq0\), we can rewrite the equation as: \(x-1=4\)
b) Negative: if \((x-1)<0\), we can rewrite the equation as: \(-(x-1)=4\)
We can also think about conditions like graphics. \(x=1\) is a key point in which the expression under modulus equals zero. All points right are the first condition \((x>1)\) and all points left are second condition \((x<1)\).
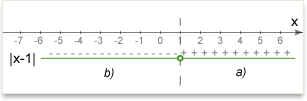
2. Solve new equations:
a) \(x-1=4\) --> x=5
b) \(-x+1=4\) --> x=-3
3. Check conditions for each solution:
a) \(x=5\) has to satisfy initial condition \(x-1>=0\). \(5-1=4>0\). It satisfies. Otherwise, we would have to reject x=5.
b) \(x=-3\) has to satisfy initial condition \(x-1<0\). \(-3-1=-4<0\). It satisfies. Otherwise, we would have to reject x=-3.
3-steps approach for complex problems
Let’s consider following examples,
Example #1
Q.: \(|x+3| - |4-x| = |8+x|\). How many solutions does the equation have?
Solution: There are 3 key points here: -8, -3, 4. So we have 4 conditions:
a) \(x < -8\). \(-(x+3) - (4-x) = -(8+x)\) --> \(x = -1\). We reject the solution because our condition is not satisfied (-1 is not less than -8)
b) \(-8 \leq x < -3\). \(-(x+3) - (4-x) = (8+x)\) --> \(x = -15\). We reject the solution because our condition is not satisfied (-15 is not within (-8,-3) interval.)
c) \(-3 \leq x < 4\). \((x+3) - (4-x) = (8+x)\) --> \(x = 9\). We reject the solution because our condition is not satisfied (9 is not within (-3,4) interval.)
d) \(x \geq 4\). \((x+3) + (4-x) = (8+x)\) --> \(x = -1\). We reject the solution because our condition is not satisfied (-1 is not more than 4)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
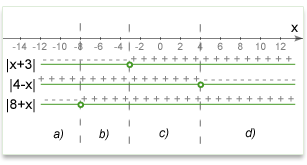
Answer: 0
Example #2
Q.: \(|x^2-4| = 1\). What is x?
Solution: There are 2 conditions:
a) \((x^2-4)\geq0\) --> \(x \leq -2\) or \(x\geq2\). \(x^2-4=1\) --> \(x^2 = 5\). x e {\(-\sqrt{5}\), \(\sqrt{5}\)} and both solutions satisfy the condition.
b) \((x^2-4)<0\) --> \(-2 < x < 2\). \(-(x^2-4) = 1\) --> \(x^2 = 3\). x e {\(-\sqrt{3}\), \(\sqrt{3}\)} and both solutions satisfy the condition.
(Optional) The following illustration may help you understand how to open modulus at different conditions.
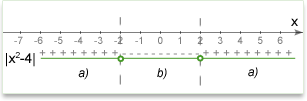
Answer: \(-\sqrt{5}\), \(-\sqrt{3}\), \(\sqrt{3}\), \(\sqrt{5}\)
Tip & Tricks
The 3-steps method works in almost all cases. At the same time, often there are shortcuts and tricks that allow you to solve absolute value problems in 10-20 sec.
I. Thinking of inequality with modulus as a segment at the number line.
For example,
Problem: 1<x<9. What inequality represents this condition?

A. |x|<3
B. |x+5|<4
C. |x-1|<9
D. |-5+x|<4
E. |3+x|<5
Solution: 10sec. Traditional 3-steps method is too time-consume technique. First of all we find length (9-1)=8 and center (1+8/2=5) of the segment represented by 1<x<9. Now, let’s look at our options. Only B and D has 8/2=4 on the right side and D had left site 0 at x=5. Therefore, answer is D.
II. Converting inequalities with modulus into a range expression.
In many cases, especially in DS problems, it helps avoid silly mistakes.
For example,
|x|<5 is equal to x e (-5,5).
|x+3|>3 is equal to x e (-inf,-6)&(0,+inf)
III. Thinking about absolute values as the distance between points at the number line.
For example,
Problem: A<X<Y<B. Is |A-X| <|X-B|?
1) |Y-A|<|B-Y|
Solution:
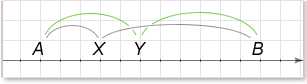
We can think of absolute values here as the distance between points. Statement 1 means than the distance between Y and A is less than that between Y and B. Because X is between A and Y, |X-A| < |Y-A| and at the same time the distance between X and B will be larger than that between Y and B (|B-Y|<|B-X|). Therefore, statement 1 is sufficient.
Pitfalls
The most typical pitfall is ignoring the third step in opening modulus - always check whether your solution satisfies conditions.
Practice Questions
Easy:
1. https://gmatclub.com/forum/which-of-the ... 44267.html
2. https://gmatclub.com/forum/if-y-is-an-i ... 39867.html
3. https://gmatclub.com/forum/on-the-numbe ... 16027.html
4. https://gmatclub.com/forum/if-k-2-m-2-w ... 07128.html
5. https://gmatclub.com/forum/if-y-0-which ... 09621.html
6. https://gmatclub.com/forum/which-of-the ... 08204.html
7. https://gmatclub.com/forum/the-function ... 96171.html
8. https://gmatclub.com/forum/4-272003.html
9. https://gmatclub.com/forum/how-many-int ... 88429.html
10. https://gmatclub.com/forum/if-x-is-a-ne ... 64088.html
Medium:
1. https://gmatclub.com/forum/what-is-the- ... 79892.html
2. https://gmatclub.com/forum/if-x-y-1-whi ... 22118.html
3. https://gmatclub.com/forum/if-x-y-0-whi ... 86959.html
4. https://gmatclub.com/forum/for-how-many ... 68675.html
5. https://gmatclub.com/forum/given-the-in ... 18973.html
6. https://gmatclub.com/forum/hot-competit ... 33254.html
7. https://gmatclub.com/forum/around-the-w ... 15784.html
8. https://gmatclub.com/forum/around-the-w ... 15984.html
9. https://gmatclub.com/forum/if-q-is-the- ... 31226.html
10. https://gmatclub.com/forum/what-is-the- ... 96176.html
Hard:
1. https://gmatclub.com/forum/if-y-x-5-x-5 ... 73626.html
2. https://gmatclub.com/forum/if-x-0-and-x ... 43572.html
3. https://gmatclub.com/forum/if-x-3-4-and ... 10071.html
4. https://gmatclub.com/forum/what-is-the- ... 98596.html
5. https://gmatclub.com/forum/how-many-roo ... 79379.html
6. https://gmatclub.com/forum/which-of-the ... 54341.html
7. https://gmatclub.com/forum/if-x-2-x-5-0 ... 24552.html
8. https://gmatclub.com/forum/what-is-the- ... 48153.html
9. https://gmatclub.com/forum/what-is-the- ... 99579.html
10. https://gmatclub.com/forum/what-is-the- ... 20033.html
lineAXYZ.png [ 8.44 KiB | Viewed 510225 times ]

line1x9.png [ 4.07 KiB | Viewed 444327 times ]

graph_modulus.png [ 7.61 KiB | Viewed 460793 times ]

Math_icon_absolute_value.png [ 1.78 KiB | Viewed 438637 times ]

Math_abs_example1.png [ 5.37 KiB | Viewed 457783 times ]

Math_abs_example2.png [ 3.67 KiB | Viewed 443998 times ]

Math_abs_example0.png [ 3.19 KiB | Viewed 446133 times ]
(Modulus)
created by: walker
edited by: bb, Bunuel
Definition
The absolute value (or modulus) \(|x|\) of a real number x is x's numerical value without regard to its sign.
For example, \(|3| = 3\); \(|-12| = 12\); \(|-1.3|=1.3\)
Graph:
Important properties:
\(|x|\geq0\)
\(|0|=0\)
\(|-x|=|x|\)
\(|x|+|y|\geq|x+y|\)
How to approach equations with moduli
It's not easy to manipulate with moduli in equations. There are two basic approaches that will help you out. Both of them are based on two ways of representing modulus as an algebraic expression.
1) \(|x| = \sqrt{x^2}\). This approach might be helpful if an equation has × and /.
2) |x| equals x if x>=0 or -x if x<0. It looks a bit complicated but it's very powerful in dealing with moduli and the most popular approach too (see below).
3-steps approach:
General approach to solving equalities and inequalities with absolute value:
1. Open modulus and set conditions.
To solve/open a modulus, you need to consider 2 situations to find all roots:
- Positive (or rather non-negative)
- Negative
For example, \(|x-1|=4\)
a) Positive: if \((x-1)\geq0\), we can rewrite the equation as: \(x-1=4\)
b) Negative: if \((x-1)<0\), we can rewrite the equation as: \(-(x-1)=4\)
We can also think about conditions like graphics. \(x=1\) is a key point in which the expression under modulus equals zero. All points right are the first condition \((x>1)\) and all points left are second condition \((x<1)\).
2. Solve new equations:
a) \(x-1=4\) --> x=5
b) \(-x+1=4\) --> x=-3
3. Check conditions for each solution:
a) \(x=5\) has to satisfy initial condition \(x-1>=0\). \(5-1=4>0\). It satisfies. Otherwise, we would have to reject x=5.
b) \(x=-3\) has to satisfy initial condition \(x-1<0\). \(-3-1=-4<0\). It satisfies. Otherwise, we would have to reject x=-3.
3-steps approach for complex problems
Let’s consider following examples,
Example #1
Q.: \(|x+3| - |4-x| = |8+x|\). How many solutions does the equation have?
Solution: There are 3 key points here: -8, -3, 4. So we have 4 conditions:
a) \(x < -8\). \(-(x+3) - (4-x) = -(8+x)\) --> \(x = -1\). We reject the solution because our condition is not satisfied (-1 is not less than -8)
b) \(-8 \leq x < -3\). \(-(x+3) - (4-x) = (8+x)\) --> \(x = -15\). We reject the solution because our condition is not satisfied (-15 is not within (-8,-3) interval.)
c) \(-3 \leq x < 4\). \((x+3) - (4-x) = (8+x)\) --> \(x = 9\). We reject the solution because our condition is not satisfied (9 is not within (-3,4) interval.)
d) \(x \geq 4\). \((x+3) + (4-x) = (8+x)\) --> \(x = -1\). We reject the solution because our condition is not satisfied (-1 is not more than 4)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
Answer: 0
Example #2
Q.: \(|x^2-4| = 1\). What is x?
Solution: There are 2 conditions:
a) \((x^2-4)\geq0\) --> \(x \leq -2\) or \(x\geq2\). \(x^2-4=1\) --> \(x^2 = 5\). x e {\(-\sqrt{5}\), \(\sqrt{5}\)} and both solutions satisfy the condition.
b) \((x^2-4)<0\) --> \(-2 < x < 2\). \(-(x^2-4) = 1\) --> \(x^2 = 3\). x e {\(-\sqrt{3}\), \(\sqrt{3}\)} and both solutions satisfy the condition.
(Optional) The following illustration may help you understand how to open modulus at different conditions.
Answer: \(-\sqrt{5}\), \(-\sqrt{3}\), \(\sqrt{3}\), \(\sqrt{5}\)
Tip & Tricks
The 3-steps method works in almost all cases. At the same time, often there are shortcuts and tricks that allow you to solve absolute value problems in 10-20 sec.
I. Thinking of inequality with modulus as a segment at the number line.
For example,
Problem: 1<x<9. What inequality represents this condition?
A. |x|<3
B. |x+5|<4
C. |x-1|<9
D. |-5+x|<4
E. |3+x|<5
Solution: 10sec. Traditional 3-steps method is too time-consume technique. First of all we find length (9-1)=8 and center (1+8/2=5) of the segment represented by 1<x<9. Now, let’s look at our options. Only B and D has 8/2=4 on the right side and D had left site 0 at x=5. Therefore, answer is D.
II. Converting inequalities with modulus into a range expression.
In many cases, especially in DS problems, it helps avoid silly mistakes.
For example,
|x|<5 is equal to x e (-5,5).
|x+3|>3 is equal to x e (-inf,-6)&(0,+inf)
III. Thinking about absolute values as the distance between points at the number line.
For example,
Problem: A<X<Y<B. Is |A-X| <|X-B|?
1) |Y-A|<|B-Y|
Solution:
We can think of absolute values here as the distance between points. Statement 1 means than the distance between Y and A is less than that between Y and B. Because X is between A and Y, |X-A| < |Y-A| and at the same time the distance between X and B will be larger than that between Y and B (|B-Y|<|B-X|). Therefore, statement 1 is sufficient.
Pitfalls
The most typical pitfall is ignoring the third step in opening modulus - always check whether your solution satisfies conditions.
Practice Questions
Easy:
1. https://gmatclub.com/forum/which-of-the ... 44267.html
2. https://gmatclub.com/forum/if-y-is-an-i ... 39867.html
3. https://gmatclub.com/forum/on-the-numbe ... 16027.html
4. https://gmatclub.com/forum/if-k-2-m-2-w ... 07128.html
5. https://gmatclub.com/forum/if-y-0-which ... 09621.html
6. https://gmatclub.com/forum/which-of-the ... 08204.html
7. https://gmatclub.com/forum/the-function ... 96171.html
8. https://gmatclub.com/forum/4-272003.html
9. https://gmatclub.com/forum/how-many-int ... 88429.html
10. https://gmatclub.com/forum/if-x-is-a-ne ... 64088.html
Medium:
1. https://gmatclub.com/forum/what-is-the- ... 79892.html
2. https://gmatclub.com/forum/if-x-y-1-whi ... 22118.html
3. https://gmatclub.com/forum/if-x-y-0-whi ... 86959.html
4. https://gmatclub.com/forum/for-how-many ... 68675.html
5. https://gmatclub.com/forum/given-the-in ... 18973.html
6. https://gmatclub.com/forum/hot-competit ... 33254.html
7. https://gmatclub.com/forum/around-the-w ... 15784.html
8. https://gmatclub.com/forum/around-the-w ... 15984.html
9. https://gmatclub.com/forum/if-q-is-the- ... 31226.html
10. https://gmatclub.com/forum/what-is-the- ... 96176.html
Hard:
1. https://gmatclub.com/forum/if-y-x-5-x-5 ... 73626.html
2. https://gmatclub.com/forum/if-x-0-and-x ... 43572.html
3. https://gmatclub.com/forum/if-x-3-4-and ... 10071.html
4. https://gmatclub.com/forum/what-is-the- ... 98596.html
5. https://gmatclub.com/forum/how-many-roo ... 79379.html
6. https://gmatclub.com/forum/which-of-the ... 54341.html
7. https://gmatclub.com/forum/if-x-2-x-5-0 ... 24552.html
8. https://gmatclub.com/forum/what-is-the- ... 48153.html
9. https://gmatclub.com/forum/what-is-the- ... 99579.html
10. https://gmatclub.com/forum/what-is-the- ... 20033.html
Show SpoilerImages
Attachment:
lineAXYZ.png [ 8.44 KiB | Viewed 510225 times ]
Attachment:
line1x9.png [ 4.07 KiB | Viewed 444327 times ]
Attachment:
graph_modulus.png [ 7.61 KiB | Viewed 460793 times ]
Attachment:
Math_icon_absolute_value.png [ 1.78 KiB | Viewed 438637 times ]
Attachment:
Math_abs_example1.png [ 5.37 KiB | Viewed 457783 times ]
Attachment:
Math_abs_example2.png [ 3.67 KiB | Viewed 443998 times ]
Attachment:
Math_abs_example0.png [ 3.19 KiB | Viewed 446133 times ]
Kudos
Bookmarks
A couple of figures to see what modulus means.
It is quite convenient to remember the definition of modulus. |x| is the distance of x from 0 on the number line.
So if |x| = 1, we are looking for points which are at a distance 1 away from 0.
If |x| < 1, we are looking for points which are at a distance less than 1 away from 0.
If |x| > 1, we are looking for points which are at a distance more than 1 away from 0.
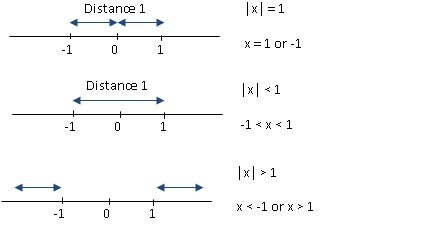
Ques1.jpg [ 14.57 KiB | Viewed 201253 times ]
If |x - 5| < 4, now we are looking for points at a distance less than 4 away from 5.
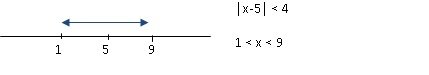
Ques2.jpg [ 4.35 KiB | Viewed 200683 times ]
It is quite convenient to remember the definition of modulus. |x| is the distance of x from 0 on the number line.
So if |x| = 1, we are looking for points which are at a distance 1 away from 0.
If |x| < 1, we are looking for points which are at a distance less than 1 away from 0.
If |x| > 1, we are looking for points which are at a distance more than 1 away from 0.
Attachment:
Ques1.jpg [ 14.57 KiB | Viewed 201253 times ]
If |x - 5| < 4, now we are looking for points at a distance less than 4 away from 5.
Attachment:
Ques2.jpg [ 4.35 KiB | Viewed 200683 times ]
Kudos
Bookmarks
10. Absolute Value
- Theory
Math: Absolute value (Modulus)
Absolute Value: Tips and hints
Properties of Absolute Values on the GMAT
Absolute modulus : A better understanding
GMAT Question Patterns: Abolute Value
The Reason Behind Absolute Value Questions on the GMAT
For more check Ultimate GMAT Quantitative Megathread










