Attachment:
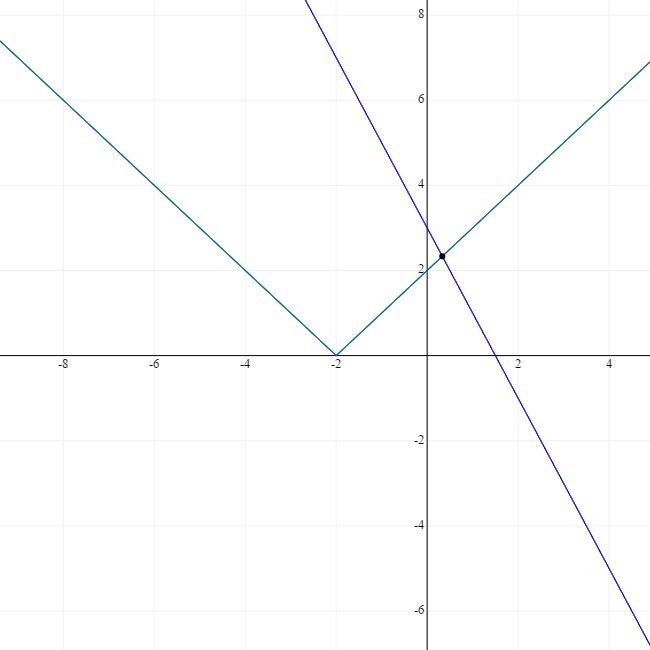
File comment: |x+2|=3-2x
 docu1.png [ 43.31 KiB | Viewed 146830 times ]
docu1.png [ 43.31 KiB | Viewed 146830 times ]
I had a PM and a profile comment asking about the absolute modulus, its concept and in particular a Question discussed on various occassion "
How many solutions does the equation |x+3|-|4-x|=|8+x| have?....
Just thought to write down few concepts I have gathered. I have not gone through various Topics on Absolute Modulus in this Forum, so maybe few points are repetition.
Although difficult for a topic like this, I'll try to follow KISS- Keep It Short and Simple. So, let me touch the concepts now..
what is absolute modulus?
Absolute modulus is the numeric value of any number without any sign or in other words ' the distance from the origin'. It will always be positive.
What kind of Qs can one see in GMAT?
The Q will ask either the values of x or how many values can x take?..
most often what one can encounter is a linear Equation with...
a) only one Mod eg.. |x+2| + 2x= 3..
b) two mods..|x+2|=|x-3|+1..
c) three mods.. very rare |x+3|-|4-x|=|8+x| ..
What are the methods
..
three methods..1) As the property suggests, Open each modulus in both +ive and -ive ....
2) Critical value
3) Graphical method..
Opening each modulus
It is a time consuming process where you open each mod in both positive and negative and the number of Equations thus formed will increase as we increase the no of mods..
a) only one Mod eg.. |x+2| + 2x= 3..
i) (x+2) + 2x=3..
3x+2=3 x=1/3.. valid value
ii) -(x+2)+2x=3..
x-2=3..x=5...
but if we substitute x=5 in |x+2| + 2x= 3..... (x+2) will turn out to be a positive value, while we took x=2 to be negative so discard
so one value of x..
b) two mods..|x+2|=|x-3|+1..
here you will have four equations..
i)(x+2)=(x-3)+1.. both positive
ii)-(x+2)=-(x-3)+1.. both negative
iii)-(x+2)=(x-3)+1..one positive and other negative
iv)(x+2)=-(x-3)+1.. opposite of the one on topc) three mods.. very rare |x+3|-|4-x|=|8+x| ..
it will further increase the number of equations..
Suggestion.. time consuming and susceptible to errors in opening of brackets and at times requires more to negate the values found as in first example.
Critical method
l
ets find what happens in this before trying the Qs as this was the main query..Step 1 :- for each mod, there is a value of x that will make that mod to 0..
Step 2 :- the minimum value of a mod will be 0 and at this value of x, the mod has the lowest value...
Once we know this critical value, we work on the mod for values lesser than(<) that or more than(>)that and including the critical value in either of them,
we assign a sign, + or -, depending on what will happen to the value inside the mod in each scenario(in one scenario it will be positive and in other, negative)..
Step 3 :- after assigning the sign, we solve for x and see if the value of x that we get is possible depending on which side of critical value we are working on..
So what are we doing hereWe are assuming a certain region for value of x and then solving for x.. If the value found matches the initial assumption, we take that as a solution or discard that value, which would mean that there is no value of x in that assumed region lets see the three examples
a) only one Mod eg.. |x+2| + 2x= 3..
here x+2 will be 0 at x=-2..
so Critical value =-2..
so two regions are <-2 and >= -2i)when x<-2, |x+2|will be given negative sign.. for this assign any value in that region say -3 in this case x+2 will become -3+2=-1 hence a negative sign..
-(x+2)+2x=3..
x-2=3.. x=5, which is not in the region <-2.. so not a valid value..
ii)when x>=-2, |x+2|will be given positive sign.. for this assign any value in that region say 3 in this case x+2 will become 3+2= 5 hence a positive sign..
(x+2)+2x=3..
3x+2=3.. x=1/3, which is in the region >=-2.. so a valid value..
b) two mods..|x+2|=|x-3|+1..
critical values -2 and 3...
so regions are <-2, -2<=x<3, x>=3..i) x<-2...x+2 will be -ive and x-3 will be negative ..
eq becomes -(x+2)=-(x-3)+1.. both negative
-x-2=-x+3+1..... no values..
ii) \(-2<=x<3\)..x+2 will be positive and x-3 will be negative ..
eq becomes (x+2)=-(x-3)+1..
x+2=-x+3+1..
x=1.. valid value
iii)x>=3..x+2 will be positive and x-3 will be positive ..
eq becomes (x+2)=(x-3)+1..
x+2=x-3+1..
no valid value..
so the solution is x=1c) three mods.. very rare |x+3|-|4-x|=|8+x| ..
its time consuming and can be solved similarly..
Graphical method
for graphical method we will have to again use the critical point..
at critical point, it is the lowest value of mod and on either side it increases with a negative slope on one side and positive slope on other sideso it forms a 'V' shape in linear equation and a 'U ' curve for Quadratic Equation..
If the mod has a negative sign in front, -|x+3|, it will have an "inverted V" shape with max value at critical value..
lets see the three examples..
a) only one Mod eg.. |x+2| + 2x= 3..
critical value at -2 and equation can be written as
|x+2| = 3-2x..
we take y=|x+2| and draw a graph and then take y=3-2x and again draw graph..
the point of intersection is our value..
 b) two mods..
b) two mods..|x+2|=|x-3|+1..
here we will take y=|x+2| and y=|x-3|+1
again the point of intersection of two sides will give us the value of x..
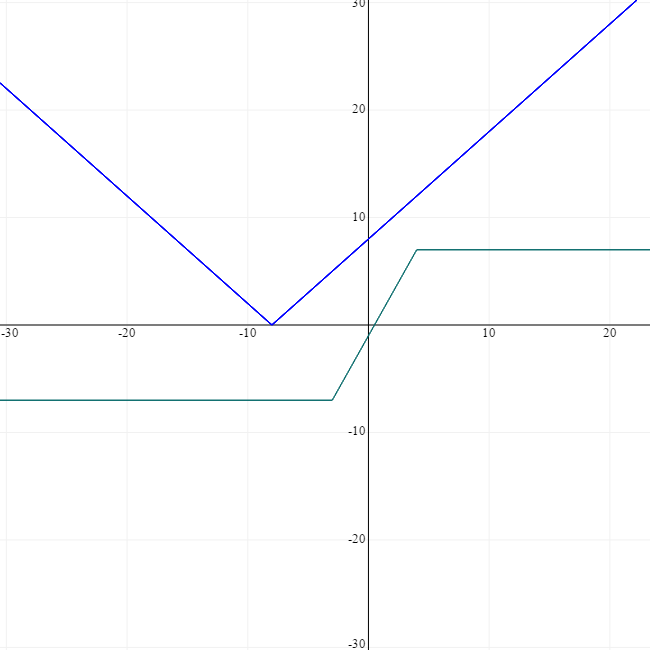
 c) three mods.. very rare
c) three mods.. very rare |x+3|-|4-x|=|8+x| ..
Here we have three critical values, but the graph will still be only two, one for LHS and one for RHS..
It will not be three for three mod as someone has drawn it in one of the discussions on this Q..
again we see the intersection of two graph..

there are no points of intersection , so no solution
THE FINER POINT
1) Opening modulus is time consuming, susceptible to error, and the answer found can still be wrong and has to checked by putting the values in mod again..
should be least priority and should be used by someone has not been able to grasp finer points of other two methods..
2) "Critical method" should be the one used in most circumstances although it requires a good understanding of signs given to the mod when opened within a region.
It has to be the method, when you are looking for values of X..
3) "Graphical method" is useful in finding the number of values of x, as getting accurate values of x may be difficult while estimating from free hand graphs..
but if understood much faster and easier to find sol for Q like
How many solutions does the equation |x+3|-|4-x|=|8+x| have?....
Hope it helps atleast a few of you..
Attachments
File comment: |x+3|-|4-x|=|8+x| ..
docu3.png [ 32.95 KiB | Viewed 144396 times ]
File comment: |x+2|=|x-3|+1..

docu2.png [ 40.42 KiB | Viewed 144413 times ]







