A, B, P, and Q are four positive numbers. Does AQ = BP?

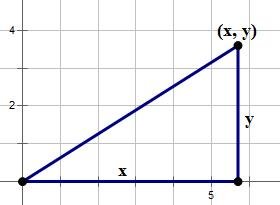
MAGOOSH OFFICIAL SOLUTION:

Big geometry idea #1: every point in the x-y plane is the vertex of a unique little right triangle with legs parallel to the axes, with a second vertex on the x-axis and the third vertex at the origin. The length of the vertical leg is the y-coordinate, and the length of the horizontal leg is the x-coordinate.

That one fact has several enormous implications. Notice, the distance from the point (x,y) to the origin is the hypotenuse, so we could find that distance with the Pythagorean Theorem.
\(distance=\sqrt{x^2+y^2}\)


This should look familiar. That’s exactly the form we have for points (A, B) and (P, Q) in statement #1. The statement:
\(\sqrt{A^2+B^2}=\sqrt{P^2+Q^2}\)
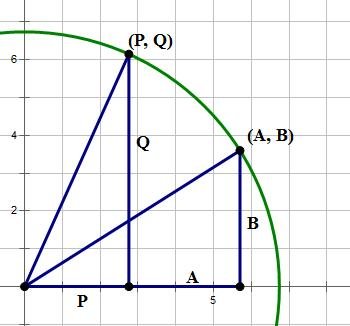
is entirely equivalent to the statement that (A, B) and (P, Q) are equal distances from the origin. In other words, if we made a circle with center at the origin, we know both points would lie on the same circle.

Well, how does this help us answer the question: Does AQ = BP? At least in the diagram as it is currently drawn, A and Q are the “big” legs and P and B are the “small” legs, and (big)*(big) ≠ (small)*(small). For this example, clearly AQ ≠ BP — a “no” answer to the prompt. But, if A = P and B = Q, the two points would be at the same place. Statement #1 would still be satisfied, and the answer to the prompt would then be “yes.” Statement #1 is consistent with both a “yes” answer and “no” answer to the prompt, so by itself it is insufficient.
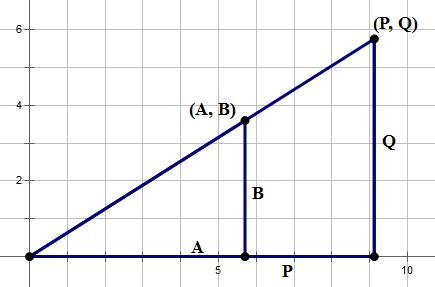
Now, forget about Statement #1 and focus exclusively on Statement #2. We are told the line through (A, B) and (P, Q) goes through the origin, like this:

Big geometry idea #2: Two triangles of the same shape and same angles but different sizes are called similar. Similar triangles have proportional sides!! That is one of the deepest and most powerful ideas in all of geometry, and it has staggering implications for problem-solving on the GMAT.

Because the two right triangles are obvious similar, we can set up a proportion among the four sides of interest:
A/B =P/Q

Now, cross-multiply:
AQ = PB

Voila! It turns out: the prompt question is a proportionality question in disguise. (will you remember that trick on the GMAT?) Statement #2 allows us to answer the prompt with a definitive “Yes!”, so it is sufficient.

Answer = B.
_________________

1) lets say A B are same as P and Q >> the statement holds and AQ=PB, however lets say we have 15,20 and 7 24 the statement holds however AQ is not equal to PB. Insufficient.
2) line passing through origin has equation of form y=m*x >>y/x=m if the line lie on line they follow this equations A/B=P/Q >> sufficient.

I think answer is B

Another way of looking at the statement 2 is, since the two points form a line that passes through the origin, we can take the slope approach.
The slope of this line should be consistent when calculated using co-ordinates of origin with each point.

Therefore, slope m=(y2-y1)/(x2-x1)

-> Q-0/P-0 = B-0/A-0
-> Q/P=B/A
-> AQ=BP

-> Sufficient

Hi Experts,
How can we deduce from statement 1 that the question is talking about x-y co-ordinate system?
Is it universal that whenever a statement like the one in stat 1 comes up, we have to consider x-y co-ordinate system?

Hello

No it is not necessary to take x-y coordinate system after looking at statement 1. If you would look at the following solution:
https://gmatclub.com/forum/a-b-p-and-q- ... l#p1490783

it is without using x-y coordinate system for statement 1

Hello from the GMAT Club BumpBot!

Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).

Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.
_________________